第8章 整式的乘除 复习(2)整式的乘除 课件(共23张PPT)
文档属性
| 名称 | 第8章 整式的乘除 复习(2)整式的乘除 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 902.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 00:00:00 | ||
图片预览








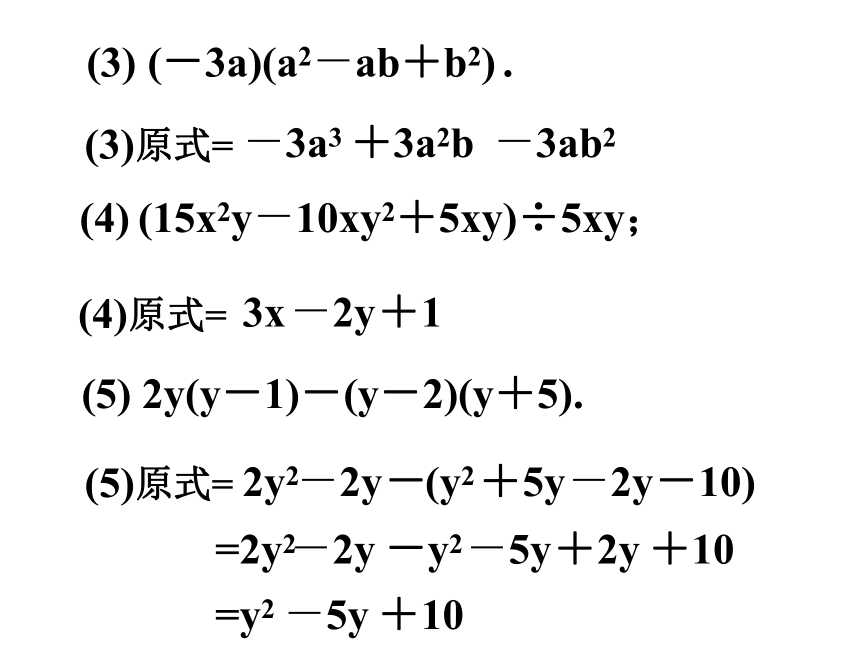
文档简介
(共23张PPT)
沪科版 七年级下册
第8章 整式的乘除 复习(2)
整式的乘除
一.整式的乘除
1.单项式与单项式相乘
单项式与单项式相乘,把系数、同底数幂分别相乘,作为积的因式,只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
知识要点
2.单项式与多项式相乘
3.多项式与多项式相乘
m(a+b+c)=ma+mb+mc.
(m+n)(a+b)=ma+mb+na+nb.
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
5.多项式除以单项式
(am+bm+cm)÷m=
am÷m
+bm÷m
+cm÷m.
4.单项式与单项式相除
单项式与单项式相除,把系数、同底数幂分别相除, 作为商的因式,只在被除式里含有的字母,则连同它的指数作为商的一个因式.
5.去括号法则:
(1) a+(b+c)=
(2) a+(b-c)=
(3) a-(b-c)=
(4) a-(b+c)=
去括号时,如果括号前是正号,去掉括号后,
括号里各项不变号.
去括号时,如果括号前是负号,去掉括号后,
括号里各项都变号.
a+b+c ;
a+b-c;
a-b+c;
a-b-c.
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
(1) a+b+c = a+(b+c);
(2) a+b-c= a+(b-c);
(3) a-b+c =a-(b-c);
(4) a-b-c =a-(b+c) .
遇“加”不变,遇“减”都变.
6.添括号法则:
二.整式的乘除典型例析
例1.计算下列各题:
(1) (-3x)2
●
4x2;
(2)-4a5b3c÷20a4b;
(3) (-3a)(a2-ab+b2) .
(4) (15x2y-10xy2+5xy)÷5xy;
(5) 2y(y-1)-(y-2)(y+5).
二.整式的乘除典型例析
例1.计算下列各题:
(1) (-3x)2
●
4x2;
(2)-20a5b3c÷5a4b;
解: (1)原式=
9x2
●
4x2
=36x4;
(2)原式=
-4ab2c
(3) (-3a)(a2-ab+b2) .
(4) (15x2y-10xy2+5xy)÷5xy;
(5) 2y(y-1)-(y-2)(y+5).
(3)原式=
-3a3
+3a2b
-3ab2
(4)原式=
3x
-2y
+1
(5)原式=
2y2
-2y
-
(y2
+5y
-2y
-10)
=2y2
-2y
-y2
+2y
-5y
+10
=y2
-5y
+10
例2.已知x2-4x-1=0,求代数式
(2x-3)2-(x+y)(x-y)-y2的值.
解:
(2x-3)2-(x+y) (x-y)-y2
=
(4x2-12x+9)
-(x2-y2)
4x2-12x+9 -x2+y2-y2
=
=
=
3x2 -12x+9
-y2
3(x2-4x+3)
∵x2-4x-1=0,
∴x2-4x =1,
∴原式=3×(1+3)
=12.
例3.一个二次三项式x2+2x+3,将它与与一个二项式相乘ax+b,积中不出现x的一次项,且二次项系数为1,求a,b的值.
解:
(x2+2x+3)
(ax+b)
=ax3+bx2
+2ax2+2bx
+3ax+3b
=ax3+(b+2a)x2
+(2b+3a)x
+3b
根据题意,得
2b+3a=0 ②
b+2a=1 ①
解方程组,得
b=-3
a=2
1.计算a2(a-2b)的结果是( )
A. a -a b B.a3-2a2b
C. a - 2ab2 D.a3- a2b2
2.下列各式计算正确的是( ).
A.(a )3=a5 B.(2a6+a4)÷a =2a3
C.a ·ab =a3b2 D.-a(-a+1)=a2-a.
三.整式的乘除练习:
(一)选择题:
B
D
3.化简m(m-2)-m2的结果是( ).
A.m B. -m C. -2m D.2m
4.下列各式计算正确的是( ).
A.2a ·a =a5
B.2ab·(a -a )=2a4b+2a b
C.(a -a)÷a=a2
D.2(a+b) ÷(a+b) =2a+2b
C
D
5.已知(x-2)(x+5)=x2+kx-10,则k的值是( ).
A.3 B. 5 C. -2 D. -3
6.若(x+1)(x2-5ax+a)的乘积中不含x2的项,
则a的值是( ).
A.5 B. C. - D. -5
A
1
5
1
5
B
6.若(2x-5)(x+3)=2x2+bx-15,则b的值是 .
(二)填空题:
7.若(2-3x)(ax+1)的乘积中不含x的一次项,
则a的值是 .
8.若(x-1)(x+1)(x+5)=x2+bx2+cx+d,则
b+d的值是 .
1
1
5
0
9.如果x2+ax-12=(x+3)(x+b),那么
a-b= .
∵(x+3)(x+b)
=x2+xb+3x+3b
∴3b=-12,
∴b=-4,
=x2+(b+3)x+3b
=b+3=-1.
3
∴a
∴a-b
=-1- (-4)
=3
10.计算:
(1) (- xy)(-3xy)2 ;
5
3
(2) y2- (y+2)(y-3) .
解:(1)原式=
(- xy) ·
5
3
=-15x3y3,
9x2y2
(2)原式=
y2-
(y2-3y+2y-6)
= y2- y2+3y-2y+6
= y+6
三.解答题:
12.计算:
(1) (8a2-4ab)÷(-4a)
(2) (12a3-6a2+3a)÷3a
=
=
8a2÷(-4a)
-4ab÷(-4a)
-2a
+b
12a3÷3a
-6a2÷3a
+3a÷3a
4a2
-2a
+1
(1)原式=
解:
原式=
13.试说明代数式:
(2x+3)(6x+2)
=12x2+4x
+18x+6
+8(7x+2)的值与
-12x2-78x
-6x(2x+13)
x的取值无关.
解:
∵(2x+3)(6x+2)
+8(7x+2)
-6x(2x+13)
+56x+16
=22
∴代数式的值与x的取值无关.
14.先化简,再求值:
(9a3b-12ab3+3ab2)÷(-3ab)
-(2b+a) ·2b,
其中a=1,b=-2.
解:
原式=
-3a2+4b2-b2
-4b2-2ab
=-3a2 -2ab -b2
当a=1,b=-2时,
原式=
-3×12 -2×1×(-2)-(-2)2
=-3+4-4
=-3.
15.在计算(2x+a)(x+b)时,甲把b看成了6,得到的结果是“2x2+8x-24”,乙错把a看成了- a,得到的结果是“2x2+14x+20”求a,b的值.
解:
∴(2x+a)
(x+6)
∵甲把b看成了6,
=2x2+12x
+ax+6a
=2x2+(12+a)x+6a
∴12+a=8
=2x2+8x-24
∴a=-4
∵乙错把a看成了-a,
∴(2x-a)
(x+b)
=2x2+2bx
-ax-ab
=2x2+(2b-a)x-ab
=2x2+14x+20
∴2b-a=14
∴b=5.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级下册
第8章 整式的乘除 复习(2)
整式的乘除
一.整式的乘除
1.单项式与单项式相乘
单项式与单项式相乘,把系数、同底数幂分别相乘,作为积的因式,只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
知识要点
2.单项式与多项式相乘
3.多项式与多项式相乘
m(a+b+c)=ma+mb+mc.
(m+n)(a+b)=ma+mb+na+nb.
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
5.多项式除以单项式
(am+bm+cm)÷m=
am÷m
+bm÷m
+cm÷m.
4.单项式与单项式相除
单项式与单项式相除,把系数、同底数幂分别相除, 作为商的因式,只在被除式里含有的字母,则连同它的指数作为商的一个因式.
5.去括号法则:
(1) a+(b+c)=
(2) a+(b-c)=
(3) a-(b-c)=
(4) a-(b+c)=
去括号时,如果括号前是正号,去掉括号后,
括号里各项不变号.
去括号时,如果括号前是负号,去掉括号后,
括号里各项都变号.
a+b+c ;
a+b-c;
a-b+c;
a-b-c.
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
(1) a+b+c = a+(b+c);
(2) a+b-c= a+(b-c);
(3) a-b+c =a-(b-c);
(4) a-b-c =a-(b+c) .
遇“加”不变,遇“减”都变.
6.添括号法则:
二.整式的乘除典型例析
例1.计算下列各题:
(1) (-3x)2
●
4x2;
(2)-4a5b3c÷20a4b;
(3) (-3a)(a2-ab+b2) .
(4) (15x2y-10xy2+5xy)÷5xy;
(5) 2y(y-1)-(y-2)(y+5).
二.整式的乘除典型例析
例1.计算下列各题:
(1) (-3x)2
●
4x2;
(2)-20a5b3c÷5a4b;
解: (1)原式=
9x2
●
4x2
=36x4;
(2)原式=
-4ab2c
(3) (-3a)(a2-ab+b2) .
(4) (15x2y-10xy2+5xy)÷5xy;
(5) 2y(y-1)-(y-2)(y+5).
(3)原式=
-3a3
+3a2b
-3ab2
(4)原式=
3x
-2y
+1
(5)原式=
2y2
-2y
-
(y2
+5y
-2y
-10)
=2y2
-2y
-y2
+2y
-5y
+10
=y2
-5y
+10
例2.已知x2-4x-1=0,求代数式
(2x-3)2-(x+y)(x-y)-y2的值.
解:
(2x-3)2-(x+y) (x-y)-y2
=
(4x2-12x+9)
-(x2-y2)
4x2-12x+9 -x2+y2-y2
=
=
=
3x2 -12x+9
-y2
3(x2-4x+3)
∵x2-4x-1=0,
∴x2-4x =1,
∴原式=3×(1+3)
=12.
例3.一个二次三项式x2+2x+3,将它与与一个二项式相乘ax+b,积中不出现x的一次项,且二次项系数为1,求a,b的值.
解:
(x2+2x+3)
(ax+b)
=ax3+bx2
+2ax2+2bx
+3ax+3b
=ax3+(b+2a)x2
+(2b+3a)x
+3b
根据题意,得
2b+3a=0 ②
b+2a=1 ①
解方程组,得
b=-3
a=2
1.计算a2(a-2b)的结果是( )
A. a -a b B.a3-2a2b
C. a - 2ab2 D.a3- a2b2
2.下列各式计算正确的是( ).
A.(a )3=a5 B.(2a6+a4)÷a =2a3
C.a ·ab =a3b2 D.-a(-a+1)=a2-a.
三.整式的乘除练习:
(一)选择题:
B
D
3.化简m(m-2)-m2的结果是( ).
A.m B. -m C. -2m D.2m
4.下列各式计算正确的是( ).
A.2a ·a =a5
B.2ab·(a -a )=2a4b+2a b
C.(a -a)÷a=a2
D.2(a+b) ÷(a+b) =2a+2b
C
D
5.已知(x-2)(x+5)=x2+kx-10,则k的值是( ).
A.3 B. 5 C. -2 D. -3
6.若(x+1)(x2-5ax+a)的乘积中不含x2的项,
则a的值是( ).
A.5 B. C. - D. -5
A
1
5
1
5
B
6.若(2x-5)(x+3)=2x2+bx-15,则b的值是 .
(二)填空题:
7.若(2-3x)(ax+1)的乘积中不含x的一次项,
则a的值是 .
8.若(x-1)(x+1)(x+5)=x2+bx2+cx+d,则
b+d的值是 .
1
1
5
0
9.如果x2+ax-12=(x+3)(x+b),那么
a-b= .
∵(x+3)(x+b)
=x2+xb+3x+3b
∴3b=-12,
∴b=-4,
=x2+(b+3)x+3b
=b+3=-1.
3
∴a
∴a-b
=-1- (-4)
=3
10.计算:
(1) (- xy)(-3xy)2 ;
5
3
(2) y2- (y+2)(y-3) .
解:(1)原式=
(- xy) ·
5
3
=-15x3y3,
9x2y2
(2)原式=
y2-
(y2-3y+2y-6)
= y2- y2+3y-2y+6
= y+6
三.解答题:
12.计算:
(1) (8a2-4ab)÷(-4a)
(2) (12a3-6a2+3a)÷3a
=
=
8a2÷(-4a)
-4ab÷(-4a)
-2a
+b
12a3÷3a
-6a2÷3a
+3a÷3a
4a2
-2a
+1
(1)原式=
解:
原式=
13.试说明代数式:
(2x+3)(6x+2)
=12x2+4x
+18x+6
+8(7x+2)的值与
-12x2-78x
-6x(2x+13)
x的取值无关.
解:
∵(2x+3)(6x+2)
+8(7x+2)
-6x(2x+13)
+56x+16
=22
∴代数式的值与x的取值无关.
14.先化简,再求值:
(9a3b-12ab3+3ab2)÷(-3ab)
-(2b+a) ·2b,
其中a=1,b=-2.
解:
原式=
-3a2+4b2-b2
-4b2-2ab
=-3a2 -2ab -b2
当a=1,b=-2时,
原式=
-3×12 -2×1×(-2)-(-2)2
=-3+4-4
=-3.
15.在计算(2x+a)(x+b)时,甲把b看成了6,得到的结果是“2x2+8x-24”,乙错把a看成了- a,得到的结果是“2x2+14x+20”求a,b的值.
解:
∴(2x+a)
(x+6)
∵甲把b看成了6,
=2x2+12x
+ax+6a
=2x2+(12+a)x+6a
∴12+a=8
=2x2+8x-24
∴a=-4
∵乙错把a看成了-a,
∴(2x-a)
(x+b)
=2x2+2bx
-ax-ab
=2x2+(2b-a)x-ab
=2x2+14x+20
∴2b-a=14
∴b=5.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
