第8章 整式的乘除 复习(3)乘法公式 课件(共24张PPT)
文档属性
| 名称 | 第8章 整式的乘除 复习(3)乘法公式 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 900.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 16:54:26 | ||
图片预览






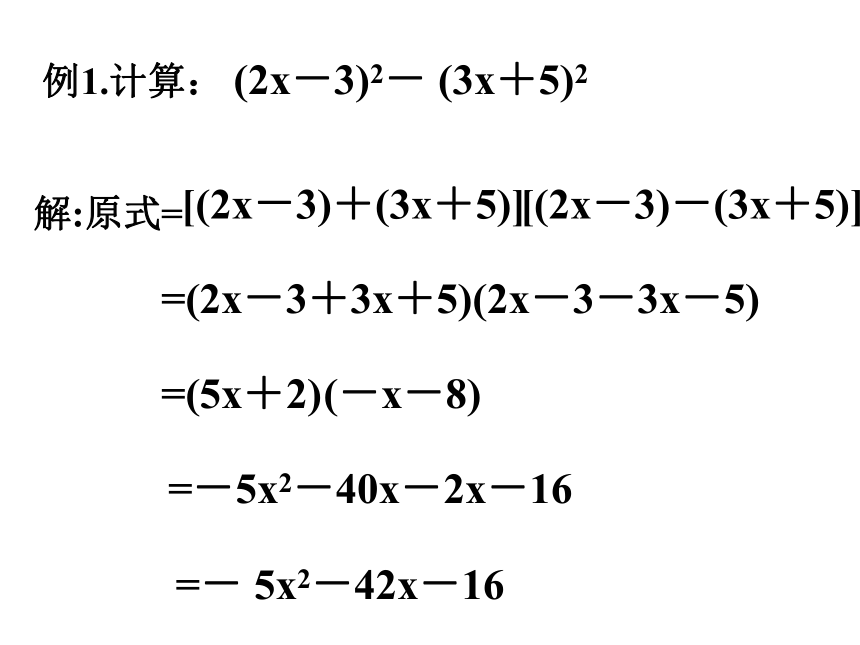


文档简介
(共24张PPT)
沪科版 七年级下册
第8章 整式的乘除 复习(3)
乘法公式
乘法公式
2.平方差公式
(a+b)(a-b)=a2-b2.
1.完全平方公式
(a+b)2=a2+2ab+b2.
(a-b)2=a2-2ab+b2.
两个数的和的平方,等于这两个数的平方和,加这两个数乘积的2倍.
两个数的差的平方,等于这两个数的平方和,减这两个数乘积的2倍.
(a+b)2 =
(a-b)2 =
a2 +2ab+b2
a2 -2ab+b2
完全平方公式
(a+b) (a-b) =a2-b2
平方差公式.
两个数的和与这两个数的差的积,
等于这两个数的平方差.
平方差公式还有如下变式:
(b+a)(a-b)=a2-b2.
(a-b)(a+b)=a2-b2.
(b+a)(-b+a)=a2-b2.
完全平方公式的常见变形
(1) a2+b2=(a+b)2-2ab
(2) a2+b2= (a-b)2+2ab
(3) (a+b)2-(a-b)2=4ab
(4) (a+b)2= (a-b)2+4ab
(5) (a-b)2= (a+b)2-4ab
例1.计算: (2x-3)2- (3x+5)2
解: 原式=
4x2-12x+9
-(9x2+30x+25)
=4x2-12x+9
- 9x2-30x-25
=- 5x2-42x-16
乘法公式典型例析
例1.计算: (2x-3)2- (3x+5)2
解:原式=
[(2x-3)-(3x+5)]
=(2x-3+3x+5)
[(2x-3)+(3x+5)]
(2x-3-3x-5)
=(5x+2)
(-x-8)
=-5x2-40x-2x-16
=- 5x2-42x-16
例2.若x+y=3,xy=1,求x2+y2的值.
∵x+y = 3,
∵xy=1,
∴(x+y)2=9,
解:
∴x2+2xy+y2=9.
∴x2+y2=
9-2xy
=
9-2
=7.
∵(2a+1)2+|1-b|=0,
解:
[(2a+b)2-(2a-b)(b+2a)]÷2b
=
[(4a2+4ab+b2)
-(4a2-b2)]
÷2b
(4a2+4ab+b2 -4a2+b2) ÷2b
=
=
(4ab+2b2) ÷2b
=
2a+b
例3.设(2a+1)2+|1-b|=0,先化简,再求值:
[(2a+b)2-(2a-b)(b+2a)]÷2b,
∴2a+1=0,
1-b=0
∴2a=-1,
b=1
∴原式=-1+1=0.
例4.利用平方差公式计算:
(1) 1020×980, (2) 20222-2021×2023.
解:
(1) 1020×980
=(1000+20)
×(1000-20)
=10002 - 202
=1000000 -400
=999600
(2) 20222-2021×2023
=20222-(2022-1)×(2022+1)
=20222-20222+1
=1
1.下列整式乘法中,能用平方差公式简便计算
的有( )
① (2a+b)(a-2b) ②(a+2b)(2b-a)
③(-a+b)(b-a) ④(-a-b)(b-a)
A.1个 B. 2个 C.3个 D. 4个
乘法公式练习
B
2.下列运算不正确的是( )
A.
B.
C. =
D.
(3x+2)(3x-2) =
9x2 -4
(x-2)2 =
x2-2x +4
(4x+y)2 =
16x2+8xy+y2
(y- )2
1
2
y2-y+
1
4
B
3.(2a+3b)(3b-2a)的结果,正确的是( )
A. B.
C. D.
9b2 -4a2
4a2-9b2
3b2 -2a2
2a2 -3b2
C
(1)已知(2x-a)2= b+4x2-12x,
4.填空:
则a= ,b= .
∵ (2x-a)2= 4x2-4ax+a2,
(2x-a)2= b+4x2-12x,
∴ -2 · 2xa= -12x,
b= a2,
∴ a= 3,
b= 32
= 9.
3
9
(2)已知(x+y)2=25, (x-y)2=9,
则x2+y2= ,
xy= .
4.填空:
17
4
x2+2xy+y2=25①
x2-2xy+y2=9 ②
提示:
①+②,得
2x2+2y2=34
①-②,得
4xy=16
5 .如果二次三项式4x2+mx+36是一个完全平方式,求m的值.
∵4x2+mx+36
=(2x)2 +mx+(±6)2,
=(2x±6)2
∴ mx= ±24x,
∴ m= ±24.
解:
6.若x-y=3,xy=10,求x2+y2的值.
∵x-y = 3,
∵xy=10,
∴(x-y)2=9,
解:
∴x2-2xy+y2=9.
∴x2+y2=
9+2xy
=
9+20
=
29.
7.计算: (2x-y)2-2(2x+y)(-2x+y)+(x+y)2
解:原式=
4x2-4xy+y2
-2(y2-4x2)
+(x2+2xy+y2)
=4x2-4xy+y2
-2y2+8x2
+x2+2xy+y2
=13x2-2xy
8.先化简,再求值:
(a+b) (2a-2b)-2(a+2b)2 ;
其中a=2,b=-1.
原式=
2a2-2b2
-2(a2+4ab+4b2)
=2a2-2b2
-2a2-8ab-8b2
=-8ab-10b2
当a=2,b=-1时,
解:原式=
-8×2× (-1)-10× (-1)2
=6
9.已知(a-b)2=8,(a+b)2=2,
求a2+b2的值.
∵ a2+b2 =(a+b)2-2ab
a2+b2 =(a-b)2+2ab
∴ 2(a2+b2) =(a+b)2+(a-b)2
=2+8 =10
∴ a2+b2 =5.
10.已知 2a-b=5,ab=1.5,
求4a2+b2-1的值.
解:
∵ 2a-b=5,
∴(2a-b)2=25,
=31
∵4a2+b2=(2a-b)2+4ab,
∴4a2+b2=25 +4×1.5
∴4a2+b2-1=30.
ab=1.5,
11.计算: 1002-992+982-972+…+22-12
解:
1002-992+982-972+…+22-12
=(100+99)
×(100-99)
+(98+97)
×(98-97)
+…+
(2+1)
×(2-1)
=100+99
+98+97
+…+
2+1
=5050.
=100+
(99+1)
+(98+2)
+(97+3)
+…+
50
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级下册
第8章 整式的乘除 复习(3)
乘法公式
乘法公式
2.平方差公式
(a+b)(a-b)=a2-b2.
1.完全平方公式
(a+b)2=a2+2ab+b2.
(a-b)2=a2-2ab+b2.
两个数的和的平方,等于这两个数的平方和,加这两个数乘积的2倍.
两个数的差的平方,等于这两个数的平方和,减这两个数乘积的2倍.
(a+b)2 =
(a-b)2 =
a2 +2ab+b2
a2 -2ab+b2
完全平方公式
(a+b) (a-b) =a2-b2
平方差公式.
两个数的和与这两个数的差的积,
等于这两个数的平方差.
平方差公式还有如下变式:
(b+a)(a-b)=a2-b2.
(a-b)(a+b)=a2-b2.
(b+a)(-b+a)=a2-b2.
完全平方公式的常见变形
(1) a2+b2=(a+b)2-2ab
(2) a2+b2= (a-b)2+2ab
(3) (a+b)2-(a-b)2=4ab
(4) (a+b)2= (a-b)2+4ab
(5) (a-b)2= (a+b)2-4ab
例1.计算: (2x-3)2- (3x+5)2
解: 原式=
4x2-12x+9
-(9x2+30x+25)
=4x2-12x+9
- 9x2-30x-25
=- 5x2-42x-16
乘法公式典型例析
例1.计算: (2x-3)2- (3x+5)2
解:原式=
[(2x-3)-(3x+5)]
=(2x-3+3x+5)
[(2x-3)+(3x+5)]
(2x-3-3x-5)
=(5x+2)
(-x-8)
=-5x2-40x-2x-16
=- 5x2-42x-16
例2.若x+y=3,xy=1,求x2+y2的值.
∵x+y = 3,
∵xy=1,
∴(x+y)2=9,
解:
∴x2+2xy+y2=9.
∴x2+y2=
9-2xy
=
9-2
=7.
∵(2a+1)2+|1-b|=0,
解:
[(2a+b)2-(2a-b)(b+2a)]÷2b
=
[(4a2+4ab+b2)
-(4a2-b2)]
÷2b
(4a2+4ab+b2 -4a2+b2) ÷2b
=
=
(4ab+2b2) ÷2b
=
2a+b
例3.设(2a+1)2+|1-b|=0,先化简,再求值:
[(2a+b)2-(2a-b)(b+2a)]÷2b,
∴2a+1=0,
1-b=0
∴2a=-1,
b=1
∴原式=-1+1=0.
例4.利用平方差公式计算:
(1) 1020×980, (2) 20222-2021×2023.
解:
(1) 1020×980
=(1000+20)
×(1000-20)
=10002 - 202
=1000000 -400
=999600
(2) 20222-2021×2023
=20222-(2022-1)×(2022+1)
=20222-20222+1
=1
1.下列整式乘法中,能用平方差公式简便计算
的有( )
① (2a+b)(a-2b) ②(a+2b)(2b-a)
③(-a+b)(b-a) ④(-a-b)(b-a)
A.1个 B. 2个 C.3个 D. 4个
乘法公式练习
B
2.下列运算不正确的是( )
A.
B.
C. =
D.
(3x+2)(3x-2) =
9x2 -4
(x-2)2 =
x2-2x +4
(4x+y)2 =
16x2+8xy+y2
(y- )2
1
2
y2-y+
1
4
B
3.(2a+3b)(3b-2a)的结果,正确的是( )
A. B.
C. D.
9b2 -4a2
4a2-9b2
3b2 -2a2
2a2 -3b2
C
(1)已知(2x-a)2= b+4x2-12x,
4.填空:
则a= ,b= .
∵ (2x-a)2= 4x2-4ax+a2,
(2x-a)2= b+4x2-12x,
∴ -2 · 2xa= -12x,
b= a2,
∴ a= 3,
b= 32
= 9.
3
9
(2)已知(x+y)2=25, (x-y)2=9,
则x2+y2= ,
xy= .
4.填空:
17
4
x2+2xy+y2=25①
x2-2xy+y2=9 ②
提示:
①+②,得
2x2+2y2=34
①-②,得
4xy=16
5 .如果二次三项式4x2+mx+36是一个完全平方式,求m的值.
∵4x2+mx+36
=(2x)2 +mx+(±6)2,
=(2x±6)2
∴ mx= ±24x,
∴ m= ±24.
解:
6.若x-y=3,xy=10,求x2+y2的值.
∵x-y = 3,
∵xy=10,
∴(x-y)2=9,
解:
∴x2-2xy+y2=9.
∴x2+y2=
9+2xy
=
9+20
=
29.
7.计算: (2x-y)2-2(2x+y)(-2x+y)+(x+y)2
解:原式=
4x2-4xy+y2
-2(y2-4x2)
+(x2+2xy+y2)
=4x2-4xy+y2
-2y2+8x2
+x2+2xy+y2
=13x2-2xy
8.先化简,再求值:
(a+b) (2a-2b)-2(a+2b)2 ;
其中a=2,b=-1.
原式=
2a2-2b2
-2(a2+4ab+4b2)
=2a2-2b2
-2a2-8ab-8b2
=-8ab-10b2
当a=2,b=-1时,
解:原式=
-8×2× (-1)-10× (-1)2
=6
9.已知(a-b)2=8,(a+b)2=2,
求a2+b2的值.
∵ a2+b2 =(a+b)2-2ab
a2+b2 =(a-b)2+2ab
∴ 2(a2+b2) =(a+b)2+(a-b)2
=2+8 =10
∴ a2+b2 =5.
10.已知 2a-b=5,ab=1.5,
求4a2+b2-1的值.
解:
∵ 2a-b=5,
∴(2a-b)2=25,
=31
∵4a2+b2=(2a-b)2+4ab,
∴4a2+b2=25 +4×1.5
∴4a2+b2-1=30.
ab=1.5,
11.计算: 1002-992+982-972+…+22-12
解:
1002-992+982-972+…+22-12
=(100+99)
×(100-99)
+(98+97)
×(98-97)
+…+
(2+1)
×(2-1)
=100+99
+98+97
+…+
2+1
=5050.
=100+
(99+1)
+(98+2)
+(97+3)
+…+
50
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
