第十七章 勾股定理 章末复习 课件(共20张PPT)
文档属性
| 名称 | 第十七章 勾股定理 章末复习 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第十七章 勾股定理
章末复习
人教版 八年级下册
教学目标
【学习目标】
1.理清本章的知识结构和重要知识点.
2.掌握本章的重要解题技巧.
【重点】
勾股定理及其逆定理的应用.
【难点】
利用勾股定理及其逆定理解决实际问题.
归纳总结
勾股定理及其应用
1.如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
A
B
C
c
a
b
公式变形
( a、b、c为正数)
归纳总结
在直角三角形中才可以运用
2.勾股定理的应用条件
3.利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
勾股定理
实际问题
转化
利用
构建
解决
直角三角形
归纳总结
4.利用勾股定理作图
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
针对训练
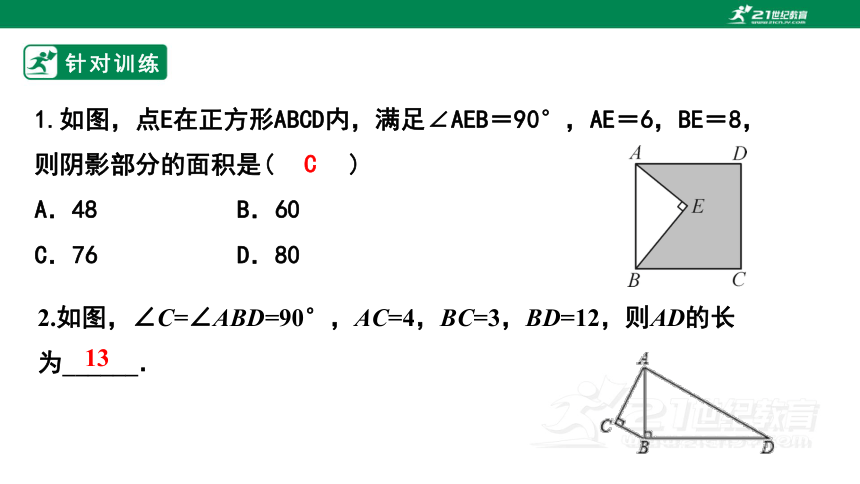
1.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60
C.76 D.80
C
2.如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD的长为______.
13
针对训练
3.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:首先画出数轴,设原点为点O,数轴上的2处表示点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB为半径作弧,设与数轴右侧交点为P,则点P的位置在数轴上( )
A.1和2之间 B.2和3之间
C.3和4之间 D.4和5之间
C
针对训练
4.如图,小华将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度为________m.
17
5.如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )
D
A. B. C. D.5
针对训练
6.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a+b= ,c=3,求△ABC的面积.
∴a2+b2+2ab=12.由题知,a2+b2=c2=9,
解:∵a+b= ,
针对训练
7.在平静的湖面上,有一棵水草,它高出水面3 dm,一阵风吹来,水草被吹到一边,草尖齐至水面,已知水草移动的水平距离为6 dm,问这里的水深是多少?
解:根据题意,作图(如图).
A
C
D
B
其中D是无风时水草的最高点,BC为湖面,AB是一阵风吹过水草的位置,则CD=3 dm,CB=6 dm,AD=AB,BC⊥AD.
在Rt△ACB中,AB2=AC2+BC2,
即(AC+3)2=AC2+62,
解得AC=4.5.
针对训练
8.如图,牧童在A处放牛,牧童家在B处,A,B处距河岸的距离AC,BD分别为500 m和300 m,且C,D两处的距离为600 m,天黑前牧童从A处将牛牵到河边去饮水,再赶回家,那么牧童最少要走多少米?
解:如图,作点B关于CD的对称点B′,连接AB′,交CD于点P,
答:牧童最少要走1 000 m.
过点A作B′B的垂线,垂足为E.
B′
P
E
在Rt△AB′E中,AE=600 m,B′E=800 m,
归纳总结
勾股定理的逆定理及其应用
1.勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,那么这个三角形是直角三角形.
A
B
C
c
a
b
注意:勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对应的角为直角.
归纳总结
满足a2 +b2=c2的三个正整数,称为勾股数.
2.勾股数
3.原命题与逆命题
如果两个命题的题设、结论正好相反,那么把其中一个叫做原命题,
另一个叫做它的逆命题.
针对训练
1.下列各组数中,是勾股数的为( )
A.1,2,3 B.4,5,6
C.3,4,5 D.7,8,9
C
2.如图,在平面直角坐标系xOy中,O是坐标原点,已知A(3,2),B(-2,3),则∠OAB=__________.
45°
针对训练
3.如图,在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C的关系,并加以证明.
解:猜想∠A+∠C=180°.
连接AC.
∵∠ABC=90°,
∴在Rt△ABC中,由勾股定理得
针对训练
3.如图,在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C的关系,并加以证明.
∵AD2+DC2=625=252=AC2,
∴△ADC是直角三角形,且∠D=90°,
∵∠DAB+∠B+∠BCD+∠D=360°,
∴∠DAB+∠BCD=180°,
即∠A+∠C=180°.
针对训练
4.一种机器零件的形状如图所示,按规定,这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸在图中已标出,这个零件符合要求吗?请说明理由.
解:这个零件符合要求.理由如下:
∵AD=12,AB=9,BC=8,BD=15,CD=17,
∴AB2+AD2=BD2,BD2+BC2=DC2,
∴△ABD,△BDC是直角三角形,
且∠A=90°,∠DBC=90°.
故这个零件符合要求.
针对训练
5.如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点D与点B重合,折痕为EF,求△ABE的面积.
解:∵将长方形折叠,使点D与点B重合,
∴ED=BE.
设AE=xcm,则ED=BE=(9-x)cm,
在Rt△ABE中,
AB2+AE2=BE2,
∴32+x2=(9-x)2,
解得x=4.
∴△ABE的面积为3×4× =6(cm2).
勾股定理可以直接解决直角三角形中已知两边求第三边的问题;如果只知一边和另两边的关系时,也可用勾股定理求出未知边,这时往往要列出方程求解.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第十七章 勾股定理
章末复习
人教版 八年级下册
教学目标
【学习目标】
1.理清本章的知识结构和重要知识点.
2.掌握本章的重要解题技巧.
【重点】
勾股定理及其逆定理的应用.
【难点】
利用勾股定理及其逆定理解决实际问题.
归纳总结
勾股定理及其应用
1.如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
A
B
C
c
a
b
公式变形
( a、b、c为正数)
归纳总结
在直角三角形中才可以运用
2.勾股定理的应用条件
3.利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
勾股定理
实际问题
转化
利用
构建
解决
直角三角形
归纳总结
4.利用勾股定理作图
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
针对训练
1.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60
C.76 D.80
C
2.如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD的长为______.
13
针对训练
3.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:首先画出数轴,设原点为点O,数轴上的2处表示点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB为半径作弧,设与数轴右侧交点为P,则点P的位置在数轴上( )
A.1和2之间 B.2和3之间
C.3和4之间 D.4和5之间
C
针对训练
4.如图,小华将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度为________m.
17
5.如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )
D
A. B. C. D.5
针对训练
6.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a+b= ,c=3,求△ABC的面积.
∴a2+b2+2ab=12.由题知,a2+b2=c2=9,
解:∵a+b= ,
针对训练
7.在平静的湖面上,有一棵水草,它高出水面3 dm,一阵风吹来,水草被吹到一边,草尖齐至水面,已知水草移动的水平距离为6 dm,问这里的水深是多少?
解:根据题意,作图(如图).
A
C
D
B
其中D是无风时水草的最高点,BC为湖面,AB是一阵风吹过水草的位置,则CD=3 dm,CB=6 dm,AD=AB,BC⊥AD.
在Rt△ACB中,AB2=AC2+BC2,
即(AC+3)2=AC2+62,
解得AC=4.5.
针对训练
8.如图,牧童在A处放牛,牧童家在B处,A,B处距河岸的距离AC,BD分别为500 m和300 m,且C,D两处的距离为600 m,天黑前牧童从A处将牛牵到河边去饮水,再赶回家,那么牧童最少要走多少米?
解:如图,作点B关于CD的对称点B′,连接AB′,交CD于点P,
答:牧童最少要走1 000 m.
过点A作B′B的垂线,垂足为E.
B′
P
E
在Rt△AB′E中,AE=600 m,B′E=800 m,
归纳总结
勾股定理的逆定理及其应用
1.勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,那么这个三角形是直角三角形.
A
B
C
c
a
b
注意:勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对应的角为直角.
归纳总结
满足a2 +b2=c2的三个正整数,称为勾股数.
2.勾股数
3.原命题与逆命题
如果两个命题的题设、结论正好相反,那么把其中一个叫做原命题,
另一个叫做它的逆命题.
针对训练
1.下列各组数中,是勾股数的为( )
A.1,2,3 B.4,5,6
C.3,4,5 D.7,8,9
C
2.如图,在平面直角坐标系xOy中,O是坐标原点,已知A(3,2),B(-2,3),则∠OAB=__________.
45°
针对训练
3.如图,在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C的关系,并加以证明.
解:猜想∠A+∠C=180°.
连接AC.
∵∠ABC=90°,
∴在Rt△ABC中,由勾股定理得
针对训练
3.如图,在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C的关系,并加以证明.
∵AD2+DC2=625=252=AC2,
∴△ADC是直角三角形,且∠D=90°,
∵∠DAB+∠B+∠BCD+∠D=360°,
∴∠DAB+∠BCD=180°,
即∠A+∠C=180°.
针对训练
4.一种机器零件的形状如图所示,按规定,这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸在图中已标出,这个零件符合要求吗?请说明理由.
解:这个零件符合要求.理由如下:
∵AD=12,AB=9,BC=8,BD=15,CD=17,
∴AB2+AD2=BD2,BD2+BC2=DC2,
∴△ABD,△BDC是直角三角形,
且∠A=90°,∠DBC=90°.
故这个零件符合要求.
针对训练
5.如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点D与点B重合,折痕为EF,求△ABE的面积.
解:∵将长方形折叠,使点D与点B重合,
∴ED=BE.
设AE=xcm,则ED=BE=(9-x)cm,
在Rt△ABE中,
AB2+AE2=BE2,
∴32+x2=(9-x)2,
解得x=4.
∴△ABE的面积为3×4× =6(cm2).
勾股定理可以直接解决直角三角形中已知两边求第三边的问题;如果只知一边和另两边的关系时,也可用勾股定理求出未知边,这时往往要列出方程求解.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
