20.2平行四边形的性质 课件
图片预览






文档简介
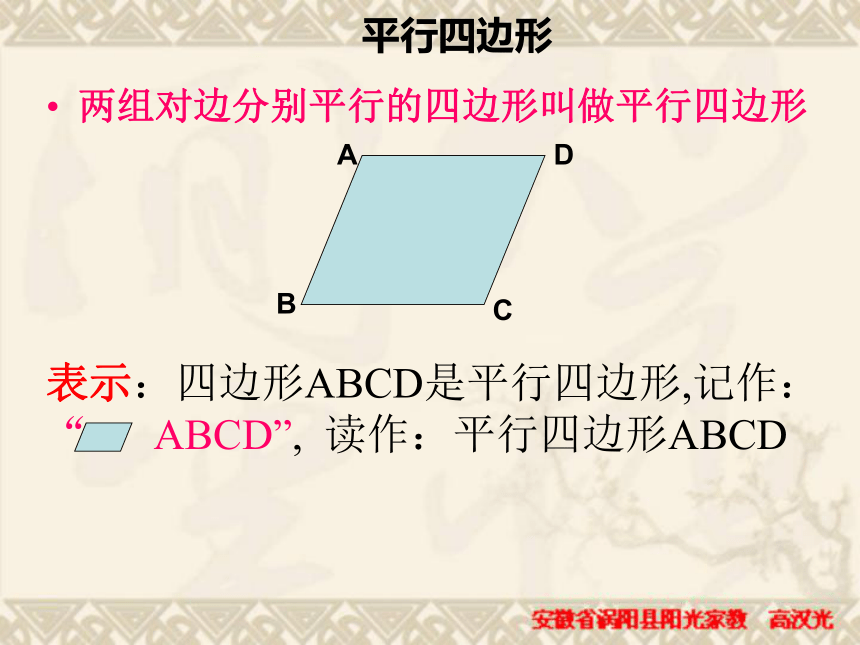
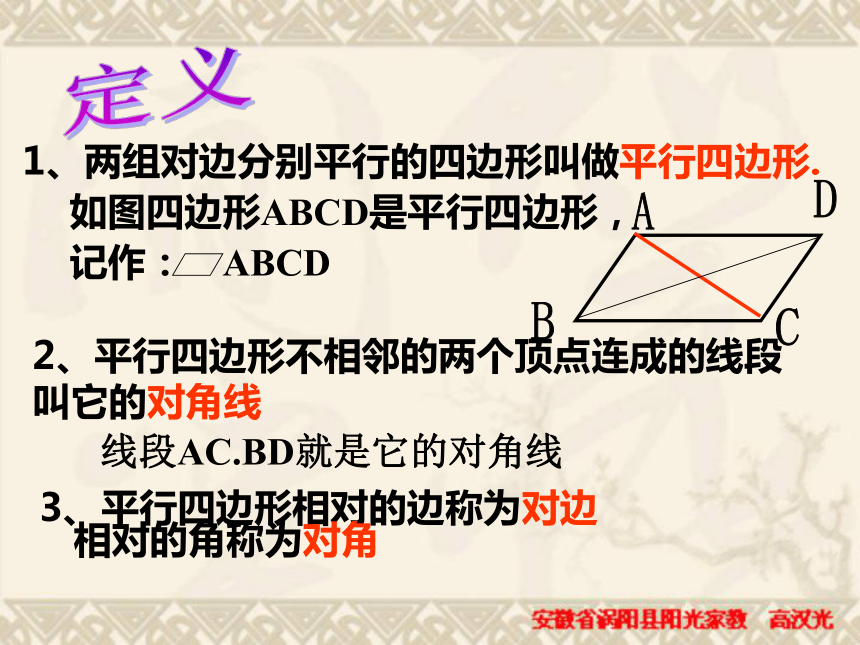
课件36张PPT。 美丽的家园,我们要好好的利用和保护她运用广泛两组对边分别平行的四边形叫做平行四边形表示:四边形ABCD是平行四边形,记作: “ ABCD”, 读作:平行四边形ABCDABCD平行四边形1、两组对边分别平行的四边形叫做平行四边形.2、平行四边形不相邻的两个顶点连成的线段
叫它的对角线线段AC.BD就是它的对角线3、平行四边形相对的边称为对边
相对的角称为对角定义 平行四边形的对边平行,相邻的
内角互为补角,此外,平行四边形还
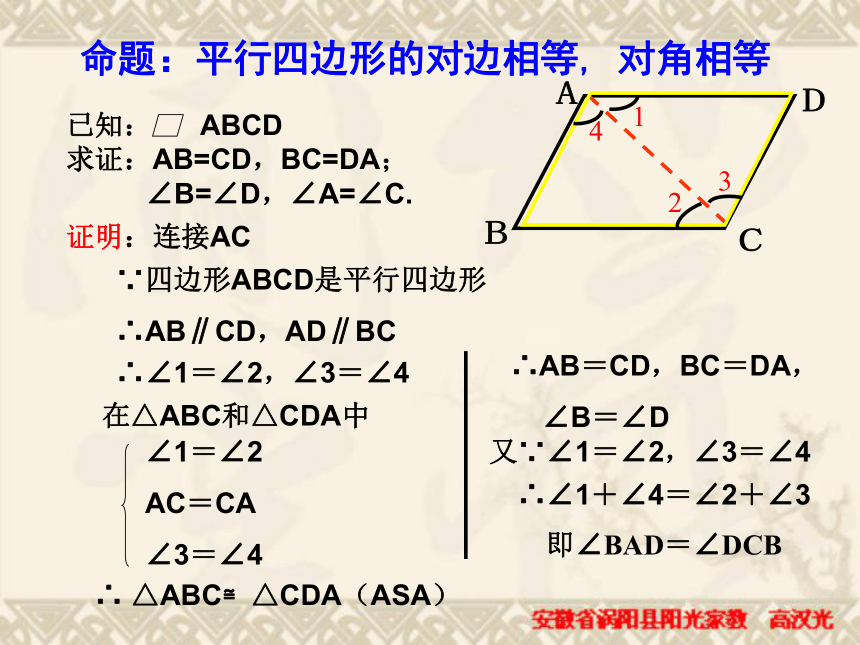
有什么性质 ?观察已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.命题:平行四边形的对边相等, 对角相等 如图:在笔直的铁轨上夹在两根铁轨之间的枕木是否一样长? 1.夹在两平行线间的平行线段相等.
2.夹在两平行线间的垂线段相等.推论ABA′B′AB、A'B':夹在两平行线间的平行线段.
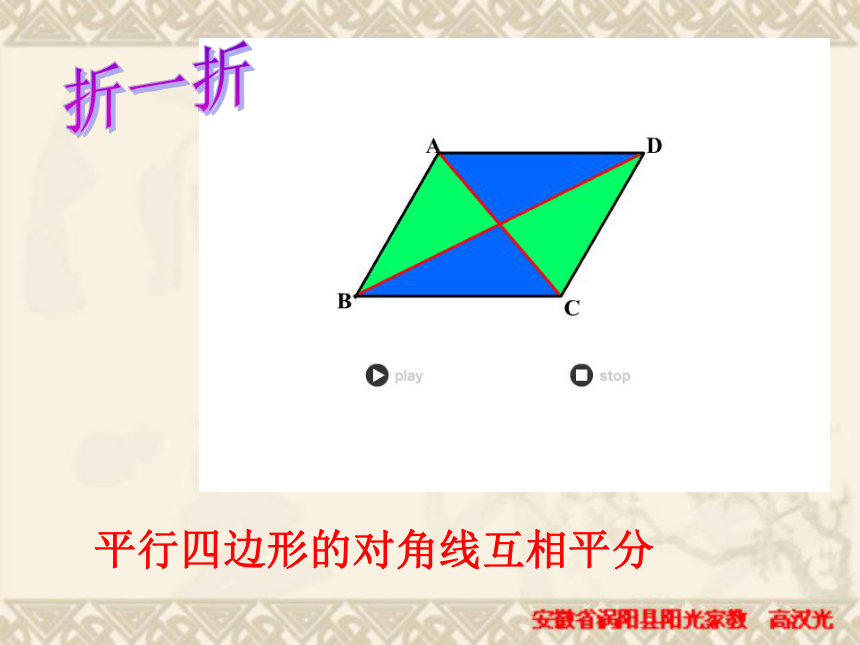
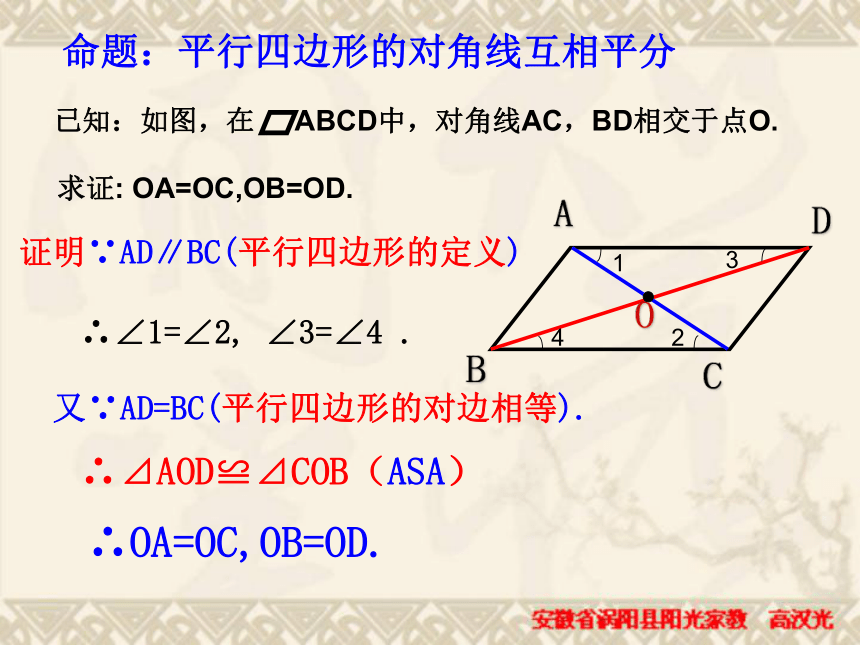
CD、C‘D’:夹在两平行线间的垂线段叫两平行线间的距离.CDC′D′平行四边形的对角线互相平分折一折BACD证明∵AD∥BC(平行四边形的定义)∴∠1=∠2, ∠3=∠4 .又∵AD=BC(平行四边形的对边相等).∴⊿AOD≌⊿COB(ASA)∴OA=OC,OB=OD. 命题:平行四边形的对角线互相平分平行四边形的性质平行且相等相等互补∠A=∠C,∠B=∠D∠A+∠B=180°互相平分AO=CO BO=DO小结例1:已知:如图,在 ABCD中,BE平分 ∠ ABC交AD于点E (1)如果AE=2,求CD的长 (2)如果∠ AED=40°,求∠ C的度数解 (1) ∵ BE平分∠ ABC ,并且AD∥BC,
∴ ∠ ABE= ∠EBC= ∠ AEB,
∴ AB=AE=2。
又 ∵CD=AB,
∴CD=2。E(2)由(1)知
∠ ABE= ∠ AEB=40°,
∴ ∠A=180°-(40°+40°)=100°。
又∵ ∠C= ∠A,
∴ ∠C =100°
任画一个三角形,你能通过平移两边后,得到一个平行四边形吗?如果能得到平形四边形,那么能得到几个?分别用字母将它们表示出来。ABCDEF画一画例2: 如图,AB∥CD,DF∥BE, AE∥CF 求证:A.B.E分别是DF,CF,DC中点。证明∵AB∥CD , DF∥BE,
∴ 四边形ABED和四边形AFBE都是平行四边形
∴AD=BE=AF ∴ A是DF中点
同理可证:B.E分别是CF,DC中点解:∵ AC⊥BC∴BC2=AB2-AC2=25=16=9(勾股定理)∴ BC=3∵ 四边形ABCD是平行四边形∴CE= AC=2,BD=2BE∴∴BD=2BE=(平行四边形对角线互相平分)(勾股定理)你还有别的方法吗? 1:在 ABCD中,已知∠A =32。,求其余三个角的度数。∵四边形ABCD是平行四边形解:且 ∠A =32。 (已知)∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等) 又∵AD∥BC(平行四边形的对边平行)∴ ∠A + ∠B =180。(两直线平行,
同旁内角互补)∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。赏析 2:已知平行四边行ABCD相邻两个角的度数比为2 :3,求平行四边行的各内角的度数。∵四边形ABCD是平行四边形解:∴ ∠A + ∠B = 180 。 ∠A = ∠c, ∠B = ∠D
又∵相邻的两个角比为2:3,则设 ∠A =2X,∠B =3X于是2X+3X=180 。。
∴ ∠ A = ∠c =2x=72。, ∠B =∠D= 3x=108 。
解得X=36。解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm解:∵四边形是平行四边形∴AB∥CD,AB=CD,AD=BC(平行四边形的性质)∴∠BAE=∠DEA(两直线平行,内错角相等)∵AE平分∠BAD∴∠BAE=∠DAE∴∠DAE=∠DEA∴DA=DE(在一个三角形中,等角对等边)同理:CF=CB∴EF=DE+CF-CD=2cm 5、已知:如图,E、F分别是平行四边形ABCD的边AD、BC上的点,且AF∥CE. 求证:DE=BF.若改成求证∠FAB=∠ECD呢?证明:如图,在平行四边形ABCD中∵AD∥BC,AF∥CE∴四边形AFCE是平行四边形(平行四边形的定义)∴AE=CF(平行四边形的对边相等)又∵AD=BC(平行四边形的对边相等)∴AD-AE=BC-CF,即 DE=BF证明∵AB∥CD∴∠ODF=∠OBE∴△DOF≌△BOE(ASA)∴OD=OB(平行四边形的对边平行)(平行四边形的对角线互相平分)∵ 四边形ABCD是平行四边形又∵∠DOF=∠BOE∴OE=OF改变直线EF的位置,OE=OF还成立吗?7:已知:在 ABCD中,BC=2AB, E点是BC的中点 求证: AE⊥DEE1234证明: ∵ E点是BC的中点
∴ BE=EC
∵ BC=2AB
∴AB=BE=EC=CD
∴∠1=∠2, ∠3=∠4
又∵ ∠1+∠2 +∠B +∠3+∠4 +∠C=180°+180°=360°,
∠B+ ∠C=180°
∴ ∠ 1+∠2+ ∠3+∠4 =180°,
∴ ∠2+∠3=90°
∵ ∠2+∠3 +∠AED =180°
∴ ∠AED=90° ∴ AE⊥DE
求证:△OBE≌△ODF证明:∵OB=OD ,OA=OC∴OE=OF.又∵ OE= OA, OF= OC(中点的定义)又∵ ∠BOE= ∠ DOF(对顶角相等)∴ △OBE≌△ODF(SAS)(平行四边形的对角线互相平分) 9:如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及 ABCD的面积. 8101.如图,四边形ABCD、DBEC都是平行四边形,那么,图中与CD相等的线段有 ;
2.如图, ABCD中,∠A=45°,BC= ,则AB与CD之间的距离是 ;若AB=3,四边形ABCD的面积是 ,ΔABD的面积是 .AB和BE(第1题图)45°131.5练一练练一练(2)若AB=4cm,则AB和DE间的距离为 _____cm(1)△ABE的面积为 ______cm22613410利用面积相等求两平行线间的距离练一练6、如图,在 ABCD中,AC与BD相交于点O,
(1)若AC=18cm,BD=24cm,则AO= , BO= .又若AB=13厘米,则△COD的周长为 。(2)若△AOB的周长为30cm, AB=12cm,则对角线AC与BD的和是 。7.如图:平行四边形ABCD中, AC、BD相交于点O, AB=8, 则以下两条线段长能作为平行四边形的对角线的长的是( )
A. 4, 12 B. 6, 8 C. 8, 26 D. 12, 209cm12cm34cm36cmD练一练59mm8练一练O(2)图中有多少对面积相等的三角形?练一练78mm13、有没有这样的平行四边形,它的两条对角线长分别为14cm和20cm,它的一边长为18cm?为什么?若平行四边形的一边长为xcm,则x的取值范围为多少?3cm<x<17cm练一练2cm或8cm练一练某市有境内一个如图四边形的小湖, 小湖的四个角A、B、C、D处恰好各有一棵古树, 在城市在景区改造中,设想把小湖面积大为原来的2倍, 并规划形状为古平行四边形,且保留4棵古树不动, 作为湖边的一个景观, 你能为园林局设想规划一下吗?应用一 一位饱经苍桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥了一块平行四边形的土地,由于年迈体弱,他决定把这块土地平均分给他的四个孩子,他的三个儿子想出了三种方案,都认为自己是对的,你说他们分得对吗?老二老三老大应用二平行四边形的邻角互补
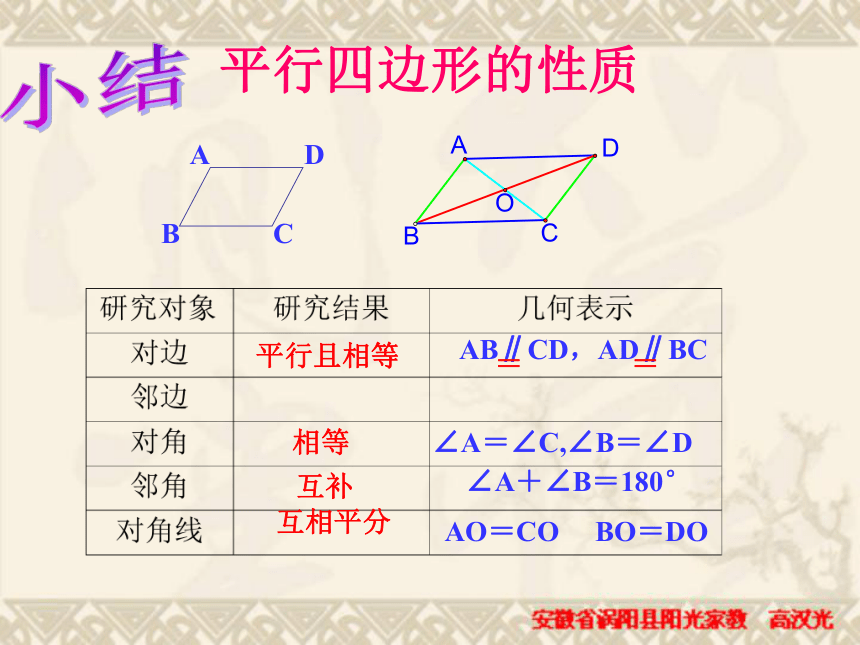
2、平行四边形的性质:1 、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形性质1:平行四边形的对边相等
性质2:平行四边形的对角相等性质3、平行四边形的对角线互相平分感悟与收获
叫它的对角线线段AC.BD就是它的对角线3、平行四边形相对的边称为对边
相对的角称为对角定义 平行四边形的对边平行,相邻的
内角互为补角,此外,平行四边形还
有什么性质 ?观察已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.命题:平行四边形的对边相等, 对角相等 如图:在笔直的铁轨上夹在两根铁轨之间的枕木是否一样长? 1.夹在两平行线间的平行线段相等.
2.夹在两平行线间的垂线段相等.推论ABA′B′AB、A'B':夹在两平行线间的平行线段.
CD、C‘D’:夹在两平行线间的垂线段叫两平行线间的距离.CDC′D′平行四边形的对角线互相平分折一折BACD证明∵AD∥BC(平行四边形的定义)∴∠1=∠2, ∠3=∠4 .又∵AD=BC(平行四边形的对边相等).∴⊿AOD≌⊿COB(ASA)∴OA=OC,OB=OD. 命题:平行四边形的对角线互相平分平行四边形的性质平行且相等相等互补∠A=∠C,∠B=∠D∠A+∠B=180°互相平分AO=CO BO=DO小结例1:已知:如图,在 ABCD中,BE平分 ∠ ABC交AD于点E (1)如果AE=2,求CD的长 (2)如果∠ AED=40°,求∠ C的度数解 (1) ∵ BE平分∠ ABC ,并且AD∥BC,
∴ ∠ ABE= ∠EBC= ∠ AEB,
∴ AB=AE=2。
又 ∵CD=AB,
∴CD=2。E(2)由(1)知
∠ ABE= ∠ AEB=40°,
∴ ∠A=180°-(40°+40°)=100°。
又∵ ∠C= ∠A,
∴ ∠C =100°
任画一个三角形,你能通过平移两边后,得到一个平行四边形吗?如果能得到平形四边形,那么能得到几个?分别用字母将它们表示出来。ABCDEF画一画例2: 如图,AB∥CD,DF∥BE, AE∥CF 求证:A.B.E分别是DF,CF,DC中点。证明∵AB∥CD , DF∥BE,
∴ 四边形ABED和四边形AFBE都是平行四边形
∴AD=BE=AF ∴ A是DF中点
同理可证:B.E分别是CF,DC中点解:∵ AC⊥BC∴BC2=AB2-AC2=25=16=9(勾股定理)∴ BC=3∵ 四边形ABCD是平行四边形∴CE= AC=2,BD=2BE∴∴BD=2BE=(平行四边形对角线互相平分)(勾股定理)你还有别的方法吗? 1:在 ABCD中,已知∠A =32。,求其余三个角的度数。∵四边形ABCD是平行四边形解:且 ∠A =32。 (已知)∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等) 又∵AD∥BC(平行四边形的对边平行)∴ ∠A + ∠B =180。(两直线平行,
同旁内角互补)∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。赏析 2:已知平行四边行ABCD相邻两个角的度数比为2 :3,求平行四边行的各内角的度数。∵四边形ABCD是平行四边形解:∴ ∠A + ∠B = 180 。 ∠A = ∠c, ∠B = ∠D
又∵相邻的两个角比为2:3,则设 ∠A =2X,∠B =3X于是2X+3X=180 。。
∴ ∠ A = ∠c =2x=72。, ∠B =∠D= 3x=108 。
解得X=36。解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm解:∵四边形是平行四边形∴AB∥CD,AB=CD,AD=BC(平行四边形的性质)∴∠BAE=∠DEA(两直线平行,内错角相等)∵AE平分∠BAD∴∠BAE=∠DAE∴∠DAE=∠DEA∴DA=DE(在一个三角形中,等角对等边)同理:CF=CB∴EF=DE+CF-CD=2cm 5、已知:如图,E、F分别是平行四边形ABCD的边AD、BC上的点,且AF∥CE. 求证:DE=BF.若改成求证∠FAB=∠ECD呢?证明:如图,在平行四边形ABCD中∵AD∥BC,AF∥CE∴四边形AFCE是平行四边形(平行四边形的定义)∴AE=CF(平行四边形的对边相等)又∵AD=BC(平行四边形的对边相等)∴AD-AE=BC-CF,即 DE=BF证明∵AB∥CD∴∠ODF=∠OBE∴△DOF≌△BOE(ASA)∴OD=OB(平行四边形的对边平行)(平行四边形的对角线互相平分)∵ 四边形ABCD是平行四边形又∵∠DOF=∠BOE∴OE=OF改变直线EF的位置,OE=OF还成立吗?7:已知:在 ABCD中,BC=2AB, E点是BC的中点 求证: AE⊥DEE1234证明: ∵ E点是BC的中点
∴ BE=EC
∵ BC=2AB
∴AB=BE=EC=CD
∴∠1=∠2, ∠3=∠4
又∵ ∠1+∠2 +∠B +∠3+∠4 +∠C=180°+180°=360°,
∠B+ ∠C=180°
∴ ∠ 1+∠2+ ∠3+∠4 =180°,
∴ ∠2+∠3=90°
∵ ∠2+∠3 +∠AED =180°
∴ ∠AED=90° ∴ AE⊥DE
求证:△OBE≌△ODF证明:∵OB=OD ,OA=OC∴OE=OF.又∵ OE= OA, OF= OC(中点的定义)又∵ ∠BOE= ∠ DOF(对顶角相等)∴ △OBE≌△ODF(SAS)(平行四边形的对角线互相平分) 9:如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及 ABCD的面积. 8101.如图,四边形ABCD、DBEC都是平行四边形,那么,图中与CD相等的线段有 ;
2.如图, ABCD中,∠A=45°,BC= ,则AB与CD之间的距离是 ;若AB=3,四边形ABCD的面积是 ,ΔABD的面积是 .AB和BE(第1题图)45°131.5练一练练一练(2)若AB=4cm,则AB和DE间的距离为 _____cm(1)△ABE的面积为 ______cm22613410利用面积相等求两平行线间的距离练一练6、如图,在 ABCD中,AC与BD相交于点O,
(1)若AC=18cm,BD=24cm,则AO= , BO= .又若AB=13厘米,则△COD的周长为 。(2)若△AOB的周长为30cm, AB=12cm,则对角线AC与BD的和是 。7.如图:平行四边形ABCD中, AC、BD相交于点O, AB=8, 则以下两条线段长能作为平行四边形的对角线的长的是( )
A. 4, 12 B. 6, 8 C. 8, 26 D. 12, 209cm12cm34cm36cmD练一练59mm8练一练O(2)图中有多少对面积相等的三角形?练一练78mm13、有没有这样的平行四边形,它的两条对角线长分别为14cm和20cm,它的一边长为18cm?为什么?若平行四边形的一边长为xcm,则x的取值范围为多少?3cm<x<17cm练一练2cm或8cm练一练某市有境内一个如图四边形的小湖, 小湖的四个角A、B、C、D处恰好各有一棵古树, 在城市在景区改造中,设想把小湖面积大为原来的2倍, 并规划形状为古平行四边形,且保留4棵古树不动, 作为湖边的一个景观, 你能为园林局设想规划一下吗?应用一 一位饱经苍桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥了一块平行四边形的土地,由于年迈体弱,他决定把这块土地平均分给他的四个孩子,他的三个儿子想出了三种方案,都认为自己是对的,你说他们分得对吗?老二老三老大应用二平行四边形的邻角互补
2、平行四边形的性质:1 、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形性质1:平行四边形的对边相等
性质2:平行四边形的对角相等性质3、平行四边形的对角线互相平分感悟与收获
