20.3矩形的性质 课件
图片预览







文档简介
课件26张PPT。矩形-----矩形的定义与性质
复习提问1.什么叫平行四边形?2. 平行四边形与四边形 有什么关系?两组对边分别平行的四边形叫做平行四边形 .特殊一般 平行四边形
具有四边形的
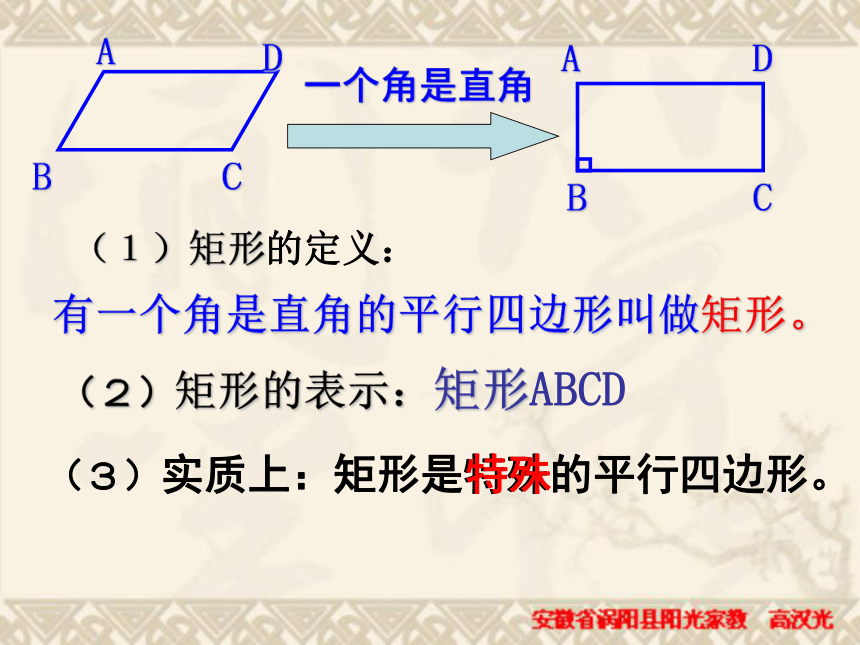
一切性质平行四边形的性质平行四边形的判定方法有一个角是直角的平行四边形叫做矩形。 (1)矩形的定义:(3)实质上:矩形是特殊的平行四边形。
特殊(2)矩形的表示:矩形ABCD一个角是直角想一想:
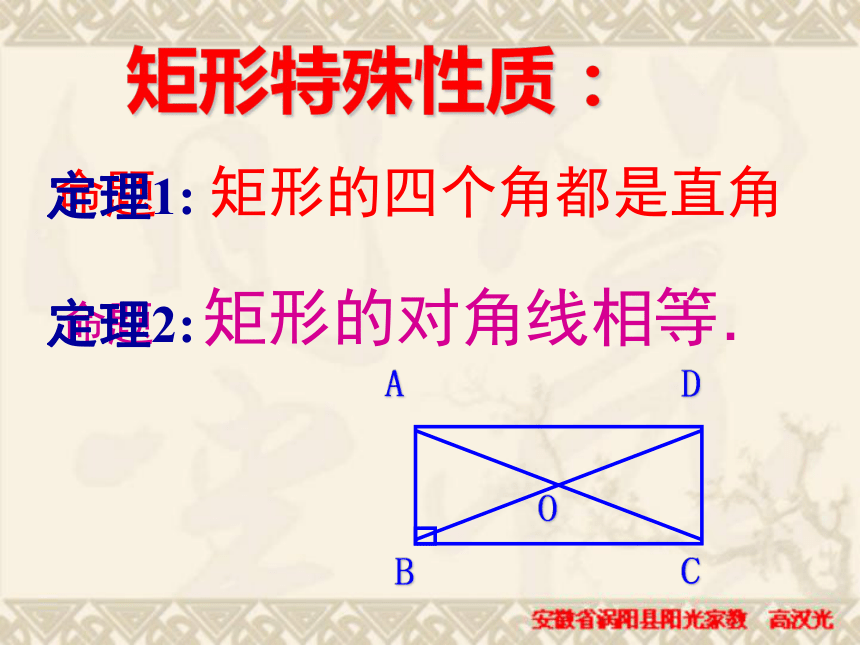
你能举出在人们的日常生活和生产实践中,有哪些东西是矩形的?矩形特殊性质:ABCD命题 矩形的对角线相等.命题 矩形的四个角都是直角定理1:定理2:命题1:矩形的四个角都是直角;已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB(SAS)∴AC = BD命题2:矩形的对角线相等;边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且平分;直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半. 如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系推论:直角三角形斜边上的中线等于斜边的一半.已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB证明:延长CD到E使DE=CD,
连结AE、BE.∵AD = BD , DE =CD
∴四边形ACBE是平行四边形E? 矩形ABCD的对角线AC、BD相交于点O,图中有多少个直角三角形?有多少个等腰三角形? 有多少对全等三角形?矩形 问题 直角三角形和等腰三角形 问题
想一想ABCDO矩形是中心对称图形,又是轴对称图形矩形是轴对称图形吗?对称轴有几条?是中心对称图形吗?探索矩形的对称性例1: 已知:矩形ABCD的两条对角线AC、BD相交于点0, ∠AOD=120°, AB = 4cm,
求(1)判断△AOB的形状;
(2)矩形对角线的长.ABCD120°O4例题赏析1.在矩形ABCD中,∠AOD=130°,则∠ACB=___
2.已知矩形的一条对角线长是8cm,两条对角
线的一个交角为60°,则矩形的边长为_______
25°做一做3.矩形ABCD中,AP⊥BD于P,BP:PD=1:3,且AC、BD相交于点O,则∠AOB的度数是_______.┓60°4.已知:如图,在矩形ABCD中, 对角线相交于点O,∠AOB=60°,AE平分∠BAC,AE交BC于E,求∠BOE的度数.30° 1. 在矩形ABCD中,对角线AC与BD相交于点O,已知AB=6,BC=8,
(1)求AC=----,BD=----,
(2)矩形ABCD的周长是------,面积是-----。
1010284868练一练2.已知△ABC是Rt△,∠ABC=Rt∠,
BD是斜边AC上的中线若BD=3㎝则AC= ㎝
2 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝,∠BDC=6510120°3.如图,矩形ABCD中, AE⊥BD,垂足为E,
∠BAE∶∠DAE=1∶3ABCDE求∠BAE,∠EAD的度数┓解:设∠BAE=X°,则∠DAE=3X°,由题意得:
X+3X=90 ° 解得,X=22.5°
即∠BAE=22.5°,∠DAE=67.5°
4.如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA=4cm.
求:BD与AD的长
解:∵四边形ABCD是矩形∴BD=AC=2OA=8cm, ∠BAD=90° 在Rt△BAD中,根据勾股定理,得: ∴答:BD=8cm, 5.已知:如图,过矩形ABCD的顶点作CE//BD,交AB的延长线于E。 求证:∠CAE=∠CEA 6.如图,将矩形纸片ABCD沿对角线BD对折,
使点A落在点E处,BE交CD于点F。已知∠ABD=30度.
求∠ABD的度数;
求证:EF=FCFE
四个角都是直
角对边平行且相
等对角线互相平
分且相等1.矩形的定义。2.矩形的性质。3.推论:直角三角形斜边上的中线等于斜边的一半感悟与收获
复习提问1.什么叫平行四边形?2. 平行四边形与四边形 有什么关系?两组对边分别平行的四边形叫做平行四边形 .特殊一般 平行四边形
具有四边形的
一切性质平行四边形的性质平行四边形的判定方法有一个角是直角的平行四边形叫做矩形。 (1)矩形的定义:(3)实质上:矩形是特殊的平行四边形。
特殊(2)矩形的表示:矩形ABCD一个角是直角想一想:
你能举出在人们的日常生活和生产实践中,有哪些东西是矩形的?矩形特殊性质:ABCD命题 矩形的对角线相等.命题 矩形的四个角都是直角定理1:定理2:命题1:矩形的四个角都是直角;已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB(SAS)∴AC = BD命题2:矩形的对角线相等;边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且平分;直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半. 如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系推论:直角三角形斜边上的中线等于斜边的一半.已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB证明:延长CD到E使DE=CD,
连结AE、BE.∵AD = BD , DE =CD
∴四边形ACBE是平行四边形E? 矩形ABCD的对角线AC、BD相交于点O,图中有多少个直角三角形?有多少个等腰三角形? 有多少对全等三角形?矩形 问题 直角三角形和等腰三角形 问题
想一想ABCDO矩形是中心对称图形,又是轴对称图形矩形是轴对称图形吗?对称轴有几条?是中心对称图形吗?探索矩形的对称性例1: 已知:矩形ABCD的两条对角线AC、BD相交于点0, ∠AOD=120°, AB = 4cm,
求(1)判断△AOB的形状;
(2)矩形对角线的长.ABCD120°O4例题赏析1.在矩形ABCD中,∠AOD=130°,则∠ACB=___
2.已知矩形的一条对角线长是8cm,两条对角
线的一个交角为60°,则矩形的边长为_______
25°做一做3.矩形ABCD中,AP⊥BD于P,BP:PD=1:3,且AC、BD相交于点O,则∠AOB的度数是_______.┓60°4.已知:如图,在矩形ABCD中, 对角线相交于点O,∠AOB=60°,AE平分∠BAC,AE交BC于E,求∠BOE的度数.30° 1. 在矩形ABCD中,对角线AC与BD相交于点O,已知AB=6,BC=8,
(1)求AC=----,BD=----,
(2)矩形ABCD的周长是------,面积是-----。
1010284868练一练2.已知△ABC是Rt△,∠ABC=Rt∠,
BD是斜边AC上的中线若BD=3㎝则AC= ㎝
2 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝,∠BDC=6510120°3.如图,矩形ABCD中, AE⊥BD,垂足为E,
∠BAE∶∠DAE=1∶3ABCDE求∠BAE,∠EAD的度数┓解:设∠BAE=X°,则∠DAE=3X°,由题意得:
X+3X=90 ° 解得,X=22.5°
即∠BAE=22.5°,∠DAE=67.5°
4.如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA=4cm.
求:BD与AD的长
解:∵四边形ABCD是矩形∴BD=AC=2OA=8cm, ∠BAD=90° 在Rt△BAD中,根据勾股定理,得: ∴答:BD=8cm, 5.已知:如图,过矩形ABCD的顶点作CE//BD,交AB的延长线于E。 求证:∠CAE=∠CEA 6.如图,将矩形纸片ABCD沿对角线BD对折,
使点A落在点E处,BE交CD于点F。已知∠ABD=30度.
求∠ABD的度数;
求证:EF=FCFE
四个角都是直
角对边平行且相
等对角线互相平
分且相等1.矩形的定义。2.矩形的性质。3.推论:直角三角形斜边上的中线等于斜边的一半感悟与收获
