20.2平行四边形的判定
图片预览




文档简介
课件43张PPT。平行四边形的对边平行且相等 平行四边形的对角线互相平分平行四边形的性质:O平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD温故知新 我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
因为AB//CD,AD//BC;
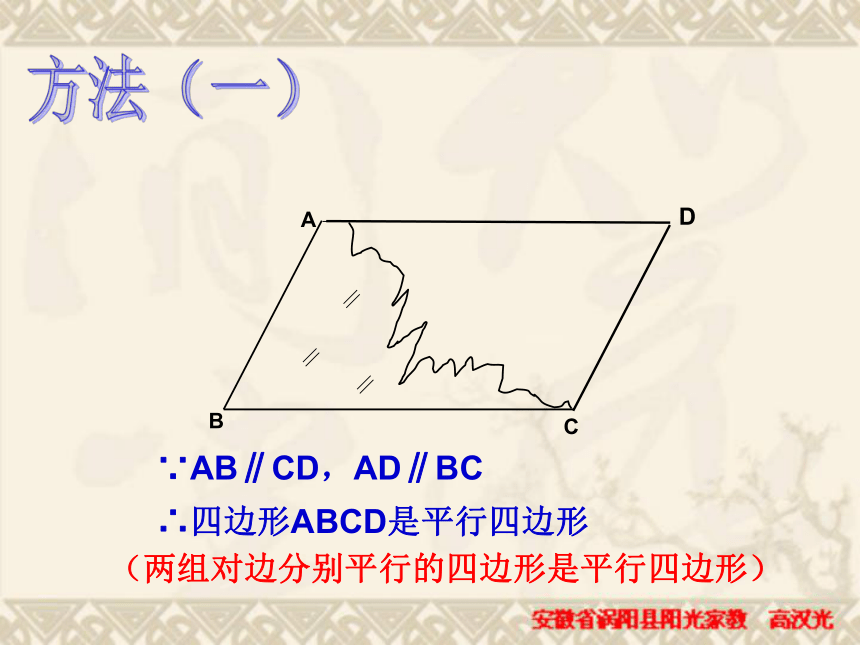
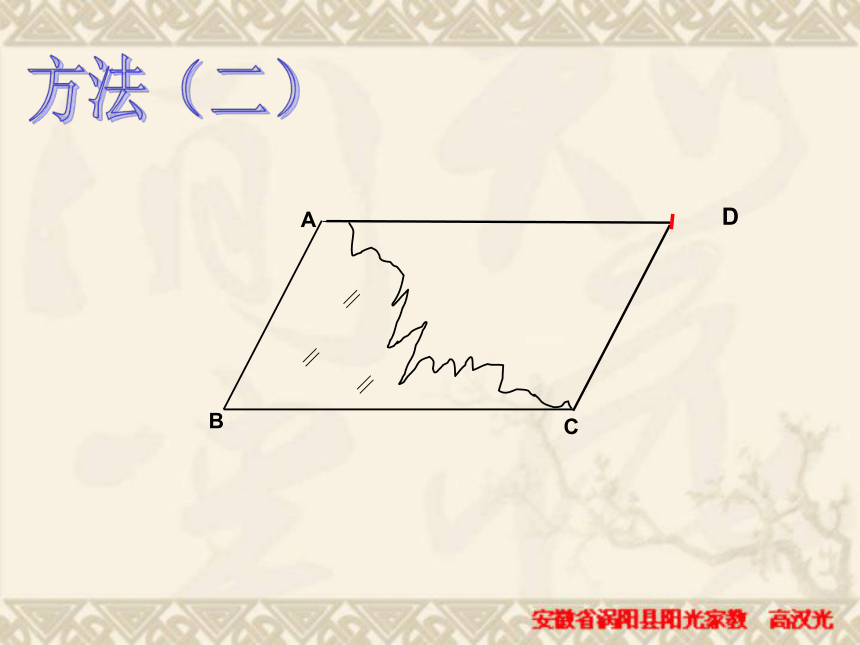
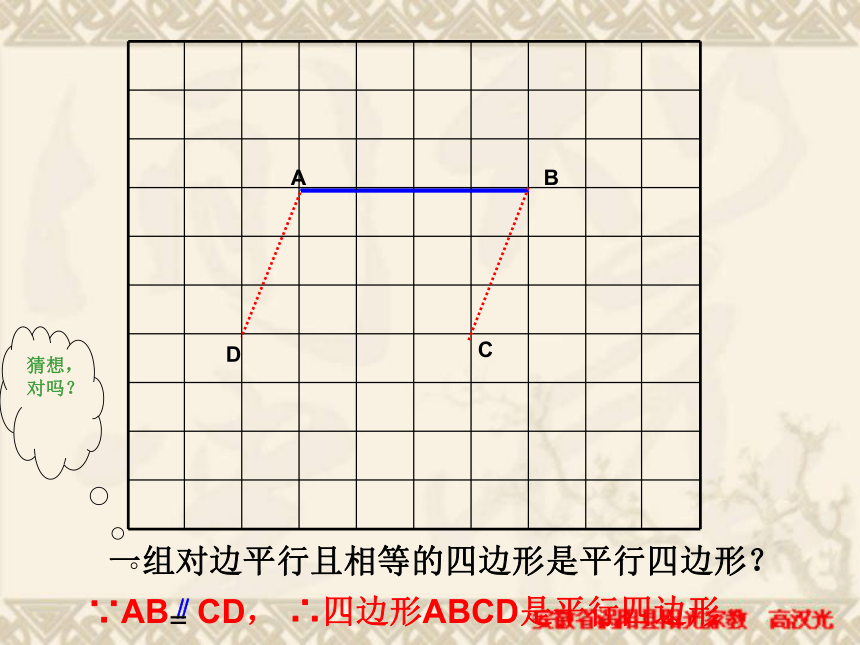
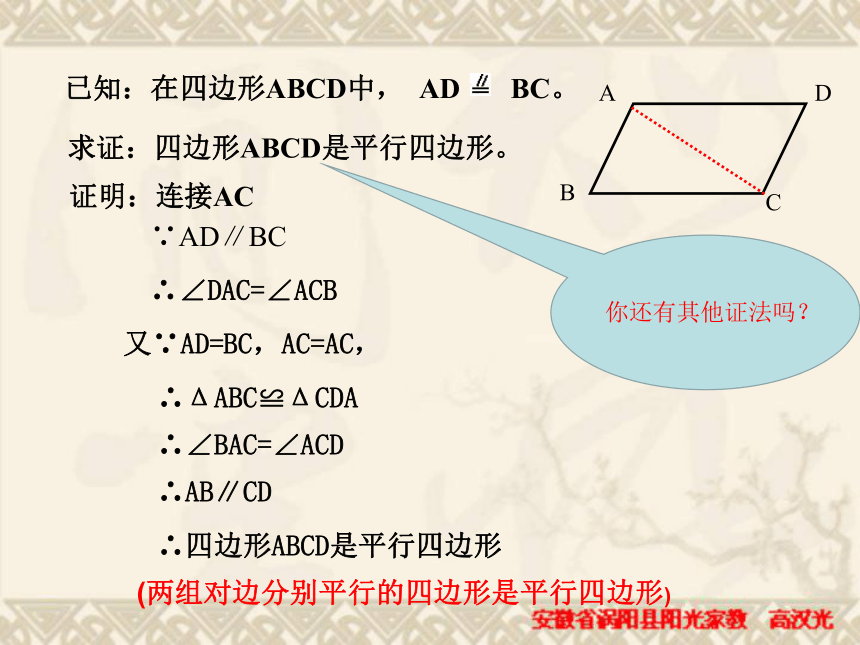
所以四边形ABCD是平行四边形。 李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)想一想方法(一)D(两组对边分别平行的四边形是平行四边形)∵AB∥CD,AD∥BC ∴四边形ABCD是平行四边形方法(二)DCD一组对边平行且相等的四边形是平行四边形?猜想,对吗?求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠DAC=∠ACB又∵AD=BC,AC=AC, ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴四边形ABCD是平行四边形 (两组对边分别平行的四边形是平行四边形)
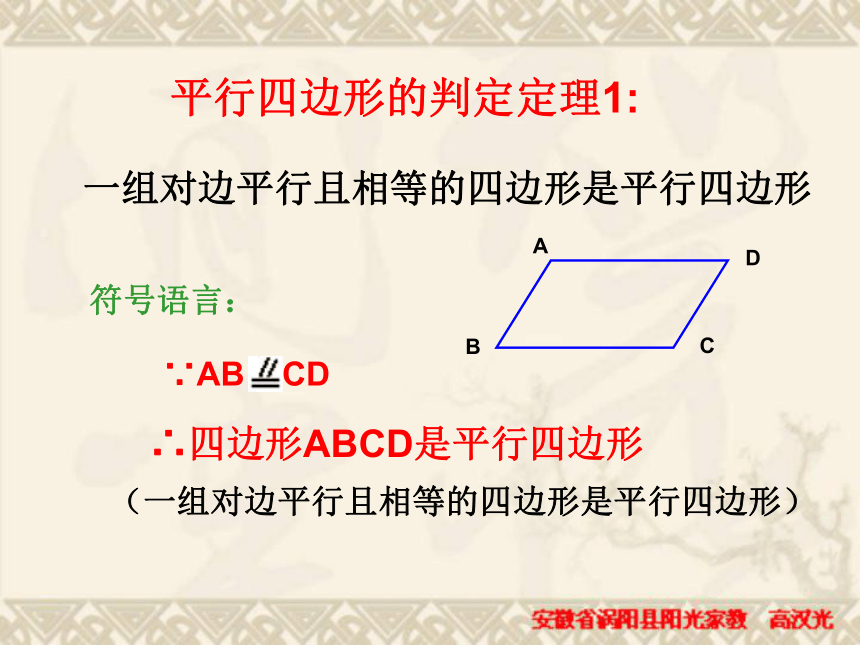
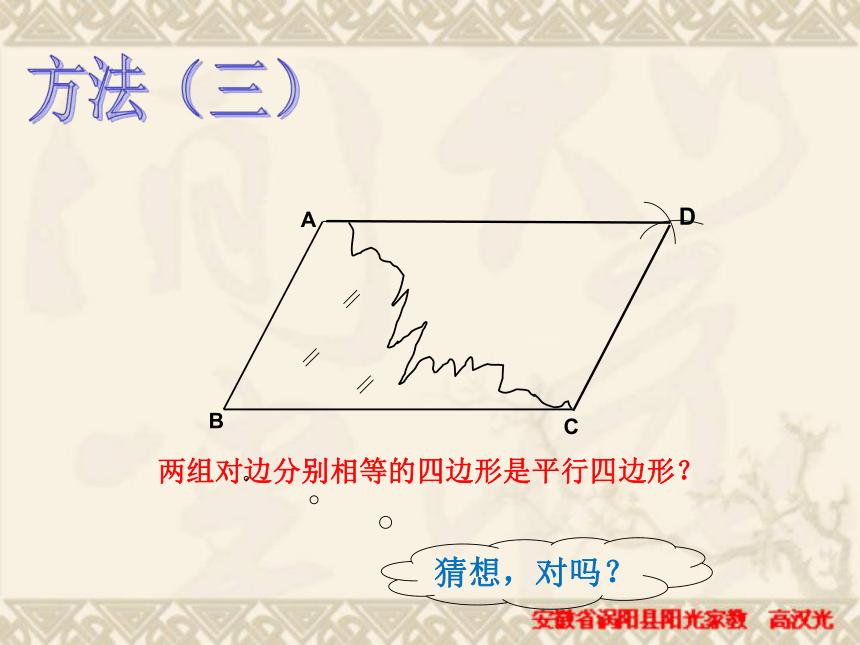
你还有其他证法吗?一组对边平行且相等的四边形是平行四边形平行四边形的判定定理1:符号语言:∵AB CD∴四边形ABCD是平行四边形 (一组对边平行且相等的四边形是平行四边形)方法(三)D两组对边分别相等的四边形是平行四边形?猜想,对吗? 两组对边分别相等的四边形是平行四边形这只是一个命题∵AB=CD,AD=BC
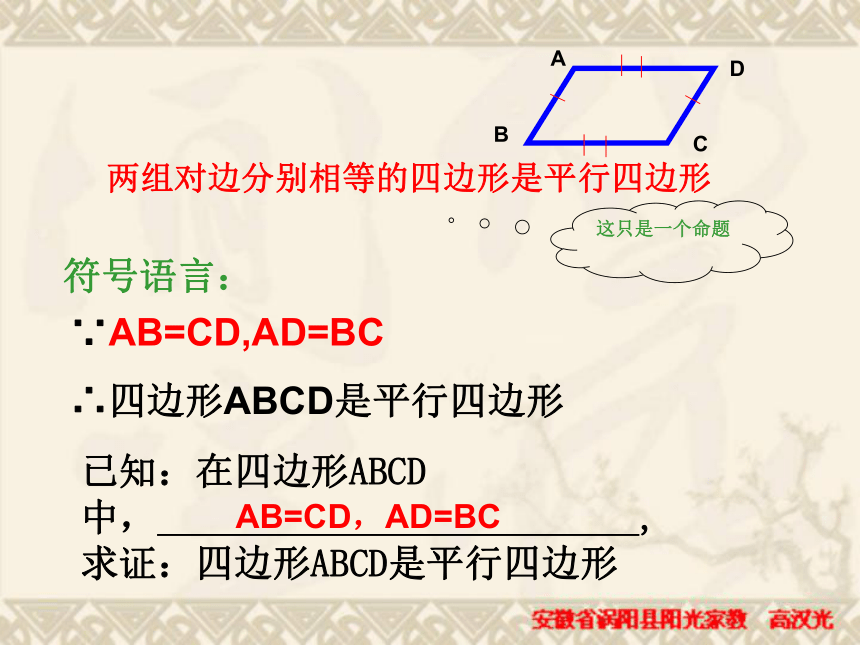
∴四边形ABCD是平行四边形已知:在四边形ABCD中, ,
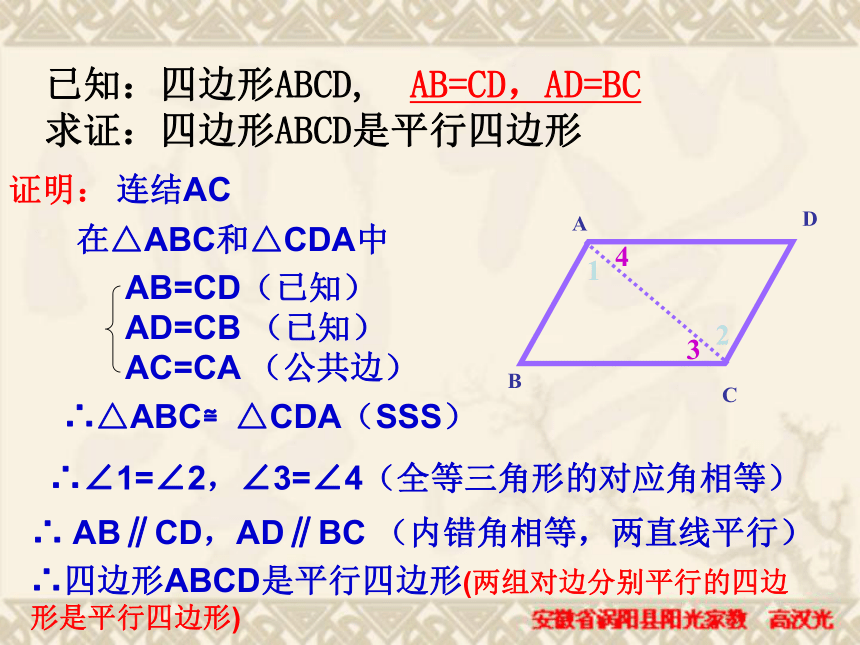
求证:四边形ABCD是平行四边形符号语言:AB=CD,AD=BC已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形平行四边形的判定定理2:符号语言:∵AB=CD,AD=BC∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)方法(四)D两组对角分别相等的四边形是平行四边形?猜想,对吗?已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
两组对角分别相等的四边形是平行四边形平行四边形的判定定理3:符号语言:∵∠A=∠C,∠B=∠D∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形)方法(五)DO对角线互相平分的四边形是平行四边形?猜想,对吗?O已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:在△AOD和△COB中∴△AOD≌△COB(SAS)
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
BAC21D(一组对边平行且相等的四边形是平行四边形)对角线互相平分的四边形是平行四边形平行四边形的判定定理4:符号语言:O∵ OA=OC,OB=OD∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形平行四边形的判定方法小结证法1: 同理可证:BE=DF 例4. 已知:E、F是平行四边形ABCD对角线AC上的两点,且AE=CF.求证:四边形BFDE是平行四边形DOABCEF证法2:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
例4. 已知:E、F是平行四边形ABCD对角线AC上的两点,且AE=CF.求证:四边形BFDE是平行四边形 例5. 求证:经过三角形一边中点与另一边平行的直线必平分第三边。
已知:D为AB中点, DE∥BC 求证:AE=CE定义:把连接三角形两边中点的线段叫做三角形的中位线例6.已知:如图,E,F分别是平行四边形 的边AD,BC的中点
求证:BE=DF.证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。∴BE=DF(平行四边形的对边分别相等)。 例7.已知:如图,E,F是平行四边形 ABCD的对角线BD上的两点,且∠BAE=∠DCF 求证:四边形AECF是平行四边形。证明:
连结AC,交BD于点O
在 平行四边形ABCD中,BO=DO,
AO=CO∵AB∥CD
∴∠ABE=∠CDF又∵∠BAE=∠CDF,AB=CD∴△ABE≌△CDF∴BE=DF∴BO-BE=DO-DF,即EO=FO∴四边形AECF是平行四边形O 1、已知在四边形ABCD中,AD∥BC,要使这个四边形为平行四边形,则需添加一个你认为正确的条件为 ( ) A B∥DC,或∠A =∠C 或AD=BC 2、能判定一个四边形是平行四边形的条件是( )A、一组对角相等 B、一组对边平行且相等
C、一对邻角互补 D、两条对角线互相垂直B3、四边形ABCD中,若∠A = ∠C,∠B = ∠D,则下列结论中错误的是( )CA、AB = CD B、AD∥BC
C、∠A = ∠B D、对角线互相平分做一做4.如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?AB ∥ DC∥ EFAD ∥ BCDE ∥ CF做一做5、请你识别下列四边形哪些是平行四边形?
为什么?⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝做一做 .6.如图,在平行四边形ABCD中,EF∥AB ,GH∥AD,EF与GH交于点O,则该图形中的平行四边形的个数共有 ( )
A 7个 B 8个 C 9 D 10个
C做一做7、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)做一做1.如图,点D、E、F分别是△ABC的边AB、
BC、CA的中点,以这些点为顶点,你在
图中画出多少个平行四边形?练一练2 . 如图.四边形AEFD和EBCF都是平行四边形,
求证:四边形ABCD是平行四边形.练一练
3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q
求证:PM=QN练一练 4、已知如图,O是 ABCD的对角线AC的中点,过点O的直线EF分别交AB、CD于E、F两点,
求证:四边形AECF是平行四边形练一练5.已知在平行四边形ABCD中,E、G分别在AB、CD上,H、F在对角线上,且AE=CG ,
AH=CF, 求证:四边形EFGH为平行四边形练一练 6.如图,在△ABC中,AB=14,BC=18,BO是AC边上的中线,求BO的取值范围。练一练7、已知△ABC,以BC为一边在点A的同侧作等边△DBC,以AC、AB为边分别向外作等边△EAC和等边△FAB。求证:四边形AEDF是平行四边形。 7、已知△ABC,以BC为一边在点A的同侧作等边△DBC,以AC、AB为边分别向外作等边△EAC和等边△FAB。求证:四边形AEDF是平行四边形。 7、已知△ABC,以BC为一边在点A的同侧作等边△DBC,以AC、AB为边分别向外作等边△EAC和等边△FAB。求证:四边形AEDF是平行四边形。 小结:1、你到今天为止共学到了几种判定平行四边形的方法?
四边形两组对边分别平行对角线互相平分一组对边平行且相等平行四边形两组对边分别相等两组对角分别相等2、三角形中位线的定义3、三角形中位线定理连接三角形两边中点的线段叫做三角形的中位线三角形的中位线平行于三角形的第三边,且等于第三边的一半4、两条平行线间的距离一条直线上的任一点到另一条直线的距离,叫做这两条平行线间的距离平行线间的距离处处相等
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD温故知新 我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
因为AB//CD,AD//BC;
所以四边形ABCD是平行四边形。 李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)想一想方法(一)D(两组对边分别平行的四边形是平行四边形)∵AB∥CD,AD∥BC ∴四边形ABCD是平行四边形方法(二)DCD一组对边平行且相等的四边形是平行四边形?猜想,对吗?求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠DAC=∠ACB又∵AD=BC,AC=AC, ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴四边形ABCD是平行四边形 (两组对边分别平行的四边形是平行四边形)
你还有其他证法吗?一组对边平行且相等的四边形是平行四边形平行四边形的判定定理1:符号语言:∵AB CD∴四边形ABCD是平行四边形 (一组对边平行且相等的四边形是平行四边形)方法(三)D两组对边分别相等的四边形是平行四边形?猜想,对吗? 两组对边分别相等的四边形是平行四边形这只是一个命题∵AB=CD,AD=BC
∴四边形ABCD是平行四边形已知:在四边形ABCD中, ,
求证:四边形ABCD是平行四边形符号语言:AB=CD,AD=BC已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形平行四边形的判定定理2:符号语言:∵AB=CD,AD=BC∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)方法(四)D两组对角分别相等的四边形是平行四边形?猜想,对吗?已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
两组对角分别相等的四边形是平行四边形平行四边形的判定定理3:符号语言:∵∠A=∠C,∠B=∠D∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形)方法(五)DO对角线互相平分的四边形是平行四边形?猜想,对吗?O已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:在△AOD和△COB中∴△AOD≌△COB(SAS)
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
BAC21D(一组对边平行且相等的四边形是平行四边形)对角线互相平分的四边形是平行四边形平行四边形的判定定理4:符号语言:O∵ OA=OC,OB=OD∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形平行四边形的判定方法小结证法1: 同理可证:BE=DF 例4. 已知:E、F是平行四边形ABCD对角线AC上的两点,且AE=CF.求证:四边形BFDE是平行四边形DOABCEF证法2:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
例4. 已知:E、F是平行四边形ABCD对角线AC上的两点,且AE=CF.求证:四边形BFDE是平行四边形 例5. 求证:经过三角形一边中点与另一边平行的直线必平分第三边。
已知:D为AB中点, DE∥BC 求证:AE=CE定义:把连接三角形两边中点的线段叫做三角形的中位线例6.已知:如图,E,F分别是平行四边形 的边AD,BC的中点
求证:BE=DF.证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。∴BE=DF(平行四边形的对边分别相等)。 例7.已知:如图,E,F是平行四边形 ABCD的对角线BD上的两点,且∠BAE=∠DCF 求证:四边形AECF是平行四边形。证明:
连结AC,交BD于点O
在 平行四边形ABCD中,BO=DO,
AO=CO∵AB∥CD
∴∠ABE=∠CDF又∵∠BAE=∠CDF,AB=CD∴△ABE≌△CDF∴BE=DF∴BO-BE=DO-DF,即EO=FO∴四边形AECF是平行四边形O 1、已知在四边形ABCD中,AD∥BC,要使这个四边形为平行四边形,则需添加一个你认为正确的条件为 ( ) A B∥DC,或∠A =∠C 或AD=BC 2、能判定一个四边形是平行四边形的条件是( )A、一组对角相等 B、一组对边平行且相等
C、一对邻角互补 D、两条对角线互相垂直B3、四边形ABCD中,若∠A = ∠C,∠B = ∠D,则下列结论中错误的是( )CA、AB = CD B、AD∥BC
C、∠A = ∠B D、对角线互相平分做一做4.如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?AB ∥ DC∥ EFAD ∥ BCDE ∥ CF做一做5、请你识别下列四边形哪些是平行四边形?
为什么?⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝做一做 .6.如图,在平行四边形ABCD中,EF∥AB ,GH∥AD,EF与GH交于点O,则该图形中的平行四边形的个数共有 ( )
A 7个 B 8个 C 9 D 10个
C做一做7、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)做一做1.如图,点D、E、F分别是△ABC的边AB、
BC、CA的中点,以这些点为顶点,你在
图中画出多少个平行四边形?练一练2 . 如图.四边形AEFD和EBCF都是平行四边形,
求证:四边形ABCD是平行四边形.练一练
3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q
求证:PM=QN练一练 4、已知如图,O是 ABCD的对角线AC的中点,过点O的直线EF分别交AB、CD于E、F两点,
求证:四边形AECF是平行四边形练一练5.已知在平行四边形ABCD中,E、G分别在AB、CD上,H、F在对角线上,且AE=CG ,
AH=CF, 求证:四边形EFGH为平行四边形练一练 6.如图,在△ABC中,AB=14,BC=18,BO是AC边上的中线,求BO的取值范围。练一练7、已知△ABC,以BC为一边在点A的同侧作等边△DBC,以AC、AB为边分别向外作等边△EAC和等边△FAB。求证:四边形AEDF是平行四边形。 7、已知△ABC,以BC为一边在点A的同侧作等边△DBC,以AC、AB为边分别向外作等边△EAC和等边△FAB。求证:四边形AEDF是平行四边形。 7、已知△ABC,以BC为一边在点A的同侧作等边△DBC,以AC、AB为边分别向外作等边△EAC和等边△FAB。求证:四边形AEDF是平行四边形。 小结:1、你到今天为止共学到了几种判定平行四边形的方法?
四边形两组对边分别平行对角线互相平分一组对边平行且相等平行四边形两组对边分别相等两组对角分别相等2、三角形中位线的定义3、三角形中位线定理连接三角形两边中点的线段叫做三角形的中位线三角形的中位线平行于三角形的第三边,且等于第三边的一半4、两条平行线间的距离一条直线上的任一点到另一条直线的距离,叫做这两条平行线间的距离平行线间的距离处处相等
