28.2.2 应用举例 第1课时 课件2021-2022学年 人教版 数学 九年级下册(共21张PPT)
文档属性
| 名称 | 28.2.2 应用举例 第1课时 课件2021-2022学年 人教版 数学 九年级下册(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 879.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 08:45:10 | ||
图片预览







文档简介
(共21张PPT)
28.2.2 应用举例
第1课时
第二十八章 锐角三角函数
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
1.了解仰角、俯角的概念,能应用锐角三角函数的知识解决有关实际问题.
2.培养学生分析问题、解决问题的能力.
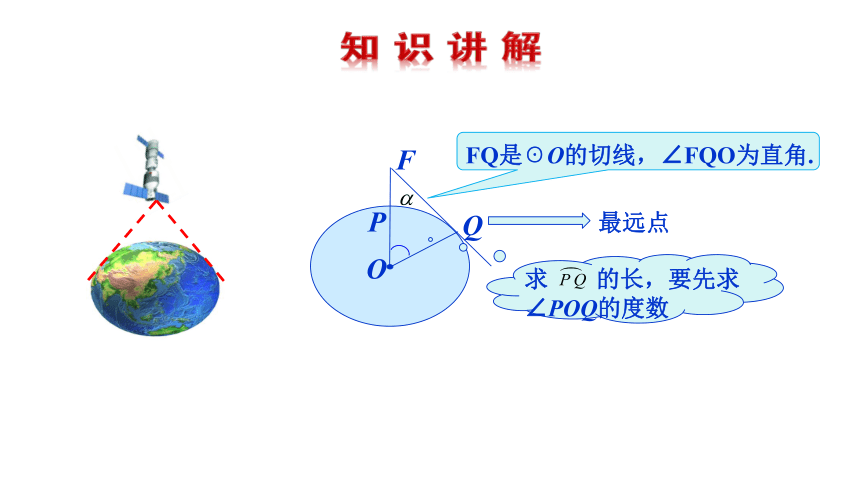
【例1】 2012年6月18日,“神舟”九号载人航天飞船与“天
宫”一号目标飞行器成功实现交会对接. “神舟”九号与“天宫”
一号的组合体在离地球表面343km的圆形轨道上运行. 如
图,当组合体运行到地球表面P点的正上方时,从中能直接
看到的地球表面最远的点在什么位置?最远点与P点的距离
是多少(地球半径约为6 400km, 结果取整数)?
O
F
P
Q
FQ是☉O的切线,∠FQO为直角.
最远点
求 的长,要先求∠POQ的度数
O
F
P
Q
设∠POQ= α ,∵FQ是☉O的切线
∴△FOQ是直角三角形.
的长为
解析:
利用解直角三角形解决实际问题的一般过程:
1.将实际问题抽象为数学问题;
画出平面图形,转化为解直角三角形的问题
2.根据条件的特点,适当选用锐角三角函数等去解
直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
归纳:
某探险者某天到达如图所示的
点A 处时,他准备估算出他
的目的地——海拔为3 500 m的山
峰顶点B处的水平距离.他能想
出一个可行的办法吗?
通过这节课的学习,相信你也行.
.
A
B
.
.
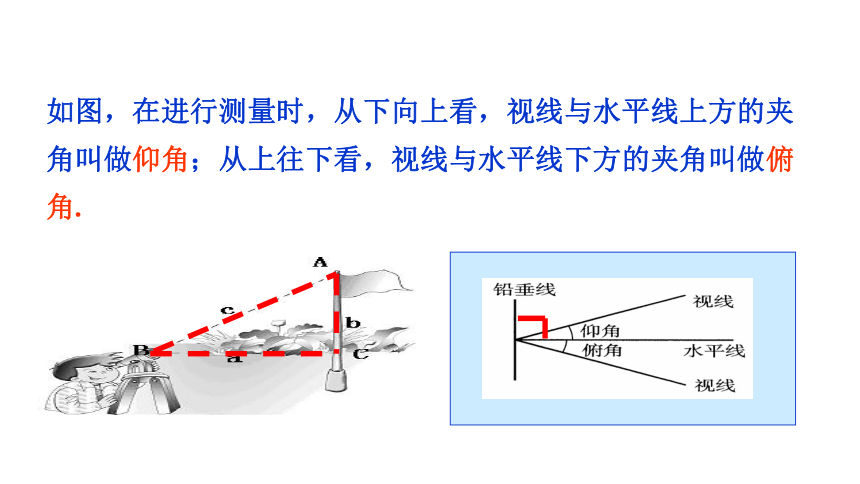
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
【例2】 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?(结果保留小数点后一位)
【分析】我们知道,在视线与水平线所成的角中,视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,ɑ =30°,β=60°.
在Rt△ABD中, ɑ =30°,AD=120,所以可以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
如图,a = 30°,β= 60°, AD=120
答:这栋楼高约为277.1m.
解析:
【例3】 如图,小明想测量塔AB的高度.他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处.测得仰角为60°,小明的身高1.5 m.那么该塔有多高 (结果精确到1 m),你能帮小明算出该塔有多高吗
D′
A
B′
B
D
C′
C
如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°,D′C′=50m.
∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50m ,设AB′=x m.
D′
A
B′
B
D
C′
C
解析:
如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,cos37 °≈0.6,
tan 37°≈0.75)
A
B
37°
45°
400米
P
【跟踪训练】
A
B
O
37°
45°
400米
P
设PO=x米,
在Rt△POB中,∠PBO=45°,
在Rt△POA中,∠PAB=37°,
OB=PO= x米.
解得x=1200.
作PO⊥AB交AB的延长线于O.
即
故飞机的高度为1200米.
解析:
利用解直角三角形解决实际问题的一般过程:
1.将实际问题抽象为数学问题;
2.根据条件的特点,适当选用锐角三角函数等去解直角三
角形;
画出平面图形,转化为解直角三角形的问题
3.得到数学问题的答案;
4.得到实际问题的答案.
1. (2021 十堰)如图,小明利用一个锐角是30°的三角板测
操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,
AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度
是( )
A. B.
C. D.
D
∴DE=AD tan∠EAD=
∴CE=CD+DE=
【解析】
由题意可得,四边形ABCD是矩形,BC=15m,AB=1.5m
∴BC=AD=15m,AB=CD=1.5m
在Rt△ADE中,∠EAD=30°,AD=15m
2.(2021 丹东)如图,一架无人机在空中A处观测到山顶B的仰角为36.87°,山顶B在水中的倒影C的俯角为63.44°,此时无人机距水面的距离AD=50米,求点B到水面距离BM的高度.(参考数据:sin36.87°≈0.60,cos36.87°≈0.80,tan36.87°≈0.75,sin63.44°≈0.89,cos63.44°≈0.45,tan63.44°≈2.00)
过点A作AH⊥BM交于BM点H,由题意可得:
AD=HM=50,设BM=x,在Rt△ABH中,
AH=BH/tan36.87°,在Rt△AHC中,
AH=CH/tan63.44°,进而可根据AH=AH,
求出x的值,即为BM的值.
【解析】
解:过点A作AH⊥BM交于BM点H,由题意可得:AD=HM=50米
设BM=x米,则MC=BM=x米
∵BH=BM-HM
∴BH=(x-50)米
∴在Rt△ABH中,AH=BH/tan36.87°≈4/3(x 50)
∵HC=HM+MC
∴HC=(50+x)米
在Rt△AHC中,AH=CH/tan63.44°≈(50+x)/2
∴4/3(x 50)= (50+x)/2 ,
解得x=110
即BM=110米
答:点B到水面距离BM的高度约为110米.
28.2.2 应用举例
第1课时
第二十八章 锐角三角函数
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
1.了解仰角、俯角的概念,能应用锐角三角函数的知识解决有关实际问题.
2.培养学生分析问题、解决问题的能力.
【例1】 2012年6月18日,“神舟”九号载人航天飞船与“天
宫”一号目标飞行器成功实现交会对接. “神舟”九号与“天宫”
一号的组合体在离地球表面343km的圆形轨道上运行. 如
图,当组合体运行到地球表面P点的正上方时,从中能直接
看到的地球表面最远的点在什么位置?最远点与P点的距离
是多少(地球半径约为6 400km, 结果取整数)?
O
F
P
Q
FQ是☉O的切线,∠FQO为直角.
最远点
求 的长,要先求∠POQ的度数
O
F
P
Q
设∠POQ= α ,∵FQ是☉O的切线
∴△FOQ是直角三角形.
的长为
解析:
利用解直角三角形解决实际问题的一般过程:
1.将实际问题抽象为数学问题;
画出平面图形,转化为解直角三角形的问题
2.根据条件的特点,适当选用锐角三角函数等去解
直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
归纳:
某探险者某天到达如图所示的
点A 处时,他准备估算出他
的目的地——海拔为3 500 m的山
峰顶点B处的水平距离.他能想
出一个可行的办法吗?
通过这节课的学习,相信你也行.
.
A
B
.
.
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
【例2】 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?(结果保留小数点后一位)
【分析】我们知道,在视线与水平线所成的角中,视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,ɑ =30°,β=60°.
在Rt△ABD中, ɑ =30°,AD=120,所以可以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
如图,a = 30°,β= 60°, AD=120
答:这栋楼高约为277.1m.
解析:
【例3】 如图,小明想测量塔AB的高度.他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处.测得仰角为60°,小明的身高1.5 m.那么该塔有多高 (结果精确到1 m),你能帮小明算出该塔有多高吗
D′
A
B′
B
D
C′
C
如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°,D′C′=50m.
∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50m ,设AB′=x m.
D′
A
B′
B
D
C′
C
解析:
如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,cos37 °≈0.6,
tan 37°≈0.75)
A
B
37°
45°
400米
P
【跟踪训练】
A
B
O
37°
45°
400米
P
设PO=x米,
在Rt△POB中,∠PBO=45°,
在Rt△POA中,∠PAB=37°,
OB=PO= x米.
解得x=1200.
作PO⊥AB交AB的延长线于O.
即
故飞机的高度为1200米.
解析:
利用解直角三角形解决实际问题的一般过程:
1.将实际问题抽象为数学问题;
2.根据条件的特点,适当选用锐角三角函数等去解直角三
角形;
画出平面图形,转化为解直角三角形的问题
3.得到数学问题的答案;
4.得到实际问题的答案.
1. (2021 十堰)如图,小明利用一个锐角是30°的三角板测
操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,
AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度
是( )
A. B.
C. D.
D
∴DE=AD tan∠EAD=
∴CE=CD+DE=
【解析】
由题意可得,四边形ABCD是矩形,BC=15m,AB=1.5m
∴BC=AD=15m,AB=CD=1.5m
在Rt△ADE中,∠EAD=30°,AD=15m
2.(2021 丹东)如图,一架无人机在空中A处观测到山顶B的仰角为36.87°,山顶B在水中的倒影C的俯角为63.44°,此时无人机距水面的距离AD=50米,求点B到水面距离BM的高度.(参考数据:sin36.87°≈0.60,cos36.87°≈0.80,tan36.87°≈0.75,sin63.44°≈0.89,cos63.44°≈0.45,tan63.44°≈2.00)
过点A作AH⊥BM交于BM点H,由题意可得:
AD=HM=50,设BM=x,在Rt△ABH中,
AH=BH/tan36.87°,在Rt△AHC中,
AH=CH/tan63.44°,进而可根据AH=AH,
求出x的值,即为BM的值.
【解析】
解:过点A作AH⊥BM交于BM点H,由题意可得:AD=HM=50米
设BM=x米,则MC=BM=x米
∵BH=BM-HM
∴BH=(x-50)米
∴在Rt△ABH中,AH=BH/tan36.87°≈4/3(x 50)
∵HC=HM+MC
∴HC=(50+x)米
在Rt△AHC中,AH=CH/tan63.44°≈(50+x)/2
∴4/3(x 50)= (50+x)/2 ,
解得x=110
即BM=110米
答:点B到水面距离BM的高度约为110米.
