第七章平面直角坐标系期末复习课件 2021—2022学年人教版数学七年级下册(共19张PPT)
文档属性
| 名称 | 第七章平面直角坐标系期末复习课件 2021—2022学年人教版数学七年级下册(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 272.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
期末复习课
第七章 平面直角坐标系
1. 平面直角坐标系:
在平面内有公共原点且互相垂直的两条数轴组成平面直角坐标系。水平的数轴为X轴,竖着的数轴为y轴,它们的公共原点O为直角坐标系的原点。
我们把有顺序的两个数a与b叫做有序数对,记做(a , b)
可用有序数对(a , b)表示平面内任一点P的坐标。a表示横坐标
,b表示纵坐标。
2.有序数对
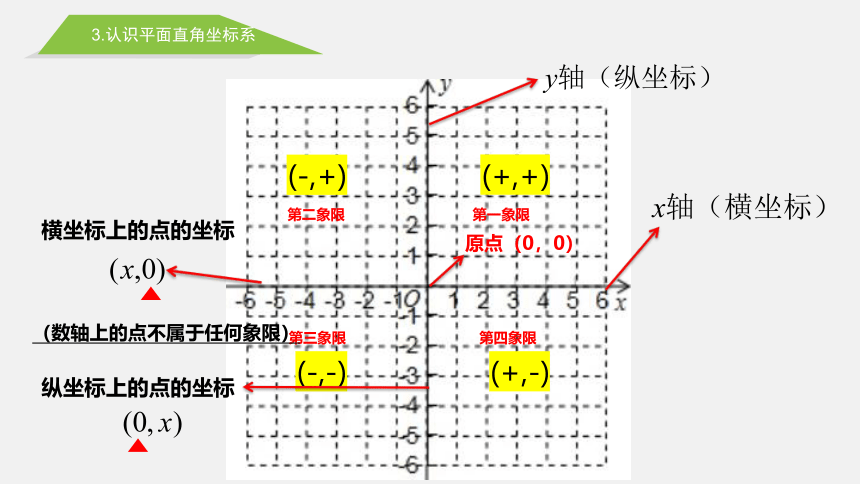
考点1:平面直角坐标系与点的坐标
原点(0,0)
(+,+)
(-,+)
(-,-)
(+,-)
第二象限
第一象限
第三象限
第四象限
横坐标上的点的坐标
纵坐标上的点的坐标
(数轴上的点不属于任何象限)
3.认识平面直角坐标系
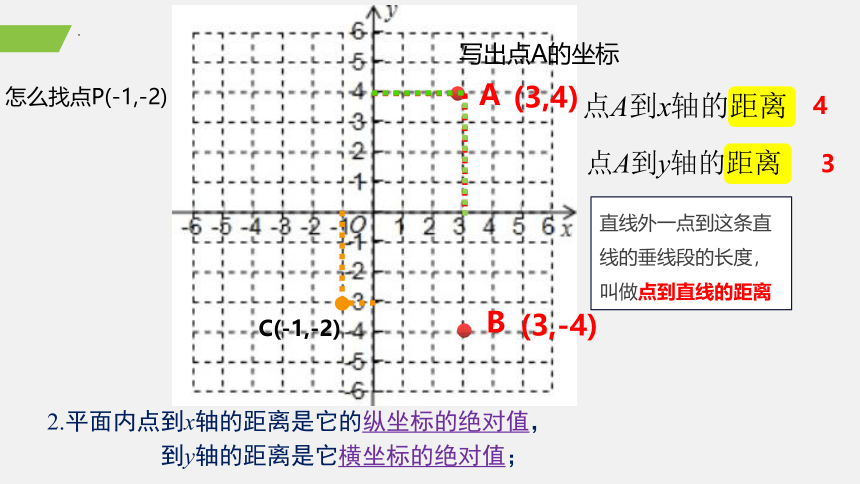
A
怎么找点P(-1,-2)
C(-1,-2)
写出点A的坐标
(3,4)
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
4
3
2.平面内点到x轴的距离是它的纵坐标的绝对值,
到y轴的距离是它横坐标的绝对值;
B
(3,-4)
【例1】已知点A(-3+a,2a+9)在第二象限,且到x轴的
距离为5,则a的值是 .
平行于 轴的直线上的点的横坐标相等
平行于 轴的直线上的点的纵坐标相等
A
(-4,4)
(0,4)
(3,4)
B
C
(5,-4)
(5,0)
D
F
【例2】已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,
则 m的值为 .
-1
【例3】直角坐标系中,在y轴上有一点P ,且OP=5,则P的坐标为 .
(0,5)或(0,-5)
考点2:坐标与平移
A(3,-3)
1)将A向上平移4个单位
B
(3,1)
纵坐标加4(-3+4=1)
2)将A向下平移2个单位
C(3,-5)
纵坐标减2(-3-2=-5)
上下平移,横坐标不变上加下减
B(3,-3)
1)将A向左平移3个单位
A(0,-3)
横坐标加3(0+3=3)
2)将A向右平移3个单位
C(-3,-3)
横坐标减-3(0-3=-3)
左右平移,纵坐标不变右加左减
当P(x ,y)向右平移a个单位长度,再向上平移b个单位长度后
坐标为p′(x+a ,y+b)。
【例4】1)将点A(1,-2)向下平移一个单位
2)将点A(1,-2)向上平移一个单位
3)将点A(1,-2)向左平移一个单位
4)将点A(1,-2)向右平移一个单位
4)将点A(1,-2)向右平移一个单位,再向上平移一个单位
A1(1,-3)
A2(1,-1)
A3(0,-2)
A4(2,-2)
A2(2,-1)
【例5】1)将点B(a,b)向下平移一个单位
2)将点B(a,b)向上平移一个单位
3)将点B(a,b)向左平移一个单位
4)将点B(a,b)向右平移一个单位
5)将点B(a,b)向右平移一个单位,再向上平移一个单位
6)将点B(a,b)向左平移两个单位,再向下平移一个单位
B1(a,b-1)
B2(a,b+1)
B3(a-1,b)
B4(a+1,b)
B1(a+1,b+1)
B6(a-1,b-1)
【例6】如图,把△ABC经过一定的变换得到△A′B′C′,
如果△ABC上点P的坐标为(a,b),那么点P变换
后的对应点P′的坐标为 .
(a+3,b+2)
你是最棒的!
将点P(-3,y)向下平移3个单位,再向左平移2个单位得到点Q(x,-1),则xy= .
-10
能力提升
考点3:求图形面积
【归纳拓展】在坐标系中求图形的面积应从两方面去把握:
(一)通常用割或补的方法将所求图形转化为一些特殊的图形.
(二)需要将已知点的坐标转化为线段的长度,以满足求面积的需要.
【例7】3.在平面直角坐标系xOy中,点A的坐标为(1. 0), 点B的坐标为(3. 2). 將点A向左平移两个单位,再向上平移 4个单位得到点C.(1)写出点C的坐标,并作出三角形ABC:(2)求三角形ABC的面积.
A(1,0)
C(-1,4)
B(3,2)
(4×2)÷2=4
(2×2)÷2=2
(4×2)÷2=4
4×4=16
4
2
2
2
4
2
解:
1)C(-1,4)
2)ABC的面积=16-4-2-4=6.
【例8】已知A(1,4),B(-4,0),C(2,0),则△ABC的面积是 .
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
利用平面直角坐标系绘制某一区域的各点分布情况的平面图包括以下过程:
(1)建立适当的坐标系,即选择适当的点作为原点,确定x轴、 y轴的正方向; (注重寻找最佳位置)
(2)根据具体问题确定恰当的比例尺,在数轴上标出单位长度;
(3)在坐标平面上画出各点,写出坐标名称。
考点4:用坐标表示地理位置
试卷12页17题(地理位置)48页19题(建立平面直角坐标系
试卷12页16题(到数轴的距离加面积)
(30页16题较简单可作为作业)
试卷52页19题(重点讲第二小题)
挑战试卷12页18题(不规则图形)
感谢您的聆听
Thank you for listening
期末复习课
第七章 平面直角坐标系
1. 平面直角坐标系:
在平面内有公共原点且互相垂直的两条数轴组成平面直角坐标系。水平的数轴为X轴,竖着的数轴为y轴,它们的公共原点O为直角坐标系的原点。
我们把有顺序的两个数a与b叫做有序数对,记做(a , b)
可用有序数对(a , b)表示平面内任一点P的坐标。a表示横坐标
,b表示纵坐标。
2.有序数对
考点1:平面直角坐标系与点的坐标
原点(0,0)
(+,+)
(-,+)
(-,-)
(+,-)
第二象限
第一象限
第三象限
第四象限
横坐标上的点的坐标
纵坐标上的点的坐标
(数轴上的点不属于任何象限)
3.认识平面直角坐标系
A
怎么找点P(-1,-2)
C(-1,-2)
写出点A的坐标
(3,4)
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
4
3
2.平面内点到x轴的距离是它的纵坐标的绝对值,
到y轴的距离是它横坐标的绝对值;
B
(3,-4)
【例1】已知点A(-3+a,2a+9)在第二象限,且到x轴的
距离为5,则a的值是 .
平行于 轴的直线上的点的横坐标相等
平行于 轴的直线上的点的纵坐标相等
A
(-4,4)
(0,4)
(3,4)
B
C
(5,-4)
(5,0)
D
F
【例2】已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,
则 m的值为 .
-1
【例3】直角坐标系中,在y轴上有一点P ,且OP=5,则P的坐标为 .
(0,5)或(0,-5)
考点2:坐标与平移
A(3,-3)
1)将A向上平移4个单位
B
(3,1)
纵坐标加4(-3+4=1)
2)将A向下平移2个单位
C(3,-5)
纵坐标减2(-3-2=-5)
上下平移,横坐标不变上加下减
B(3,-3)
1)将A向左平移3个单位
A(0,-3)
横坐标加3(0+3=3)
2)将A向右平移3个单位
C(-3,-3)
横坐标减-3(0-3=-3)
左右平移,纵坐标不变右加左减
当P(x ,y)向右平移a个单位长度,再向上平移b个单位长度后
坐标为p′(x+a ,y+b)。
【例4】1)将点A(1,-2)向下平移一个单位
2)将点A(1,-2)向上平移一个单位
3)将点A(1,-2)向左平移一个单位
4)将点A(1,-2)向右平移一个单位
4)将点A(1,-2)向右平移一个单位,再向上平移一个单位
A1(1,-3)
A2(1,-1)
A3(0,-2)
A4(2,-2)
A2(2,-1)
【例5】1)将点B(a,b)向下平移一个单位
2)将点B(a,b)向上平移一个单位
3)将点B(a,b)向左平移一个单位
4)将点B(a,b)向右平移一个单位
5)将点B(a,b)向右平移一个单位,再向上平移一个单位
6)将点B(a,b)向左平移两个单位,再向下平移一个单位
B1(a,b-1)
B2(a,b+1)
B3(a-1,b)
B4(a+1,b)
B1(a+1,b+1)
B6(a-1,b-1)
【例6】如图,把△ABC经过一定的变换得到△A′B′C′,
如果△ABC上点P的坐标为(a,b),那么点P变换
后的对应点P′的坐标为 .
(a+3,b+2)
你是最棒的!
将点P(-3,y)向下平移3个单位,再向左平移2个单位得到点Q(x,-1),则xy= .
-10
能力提升
考点3:求图形面积
【归纳拓展】在坐标系中求图形的面积应从两方面去把握:
(一)通常用割或补的方法将所求图形转化为一些特殊的图形.
(二)需要将已知点的坐标转化为线段的长度,以满足求面积的需要.
【例7】3.在平面直角坐标系xOy中,点A的坐标为(1. 0), 点B的坐标为(3. 2). 將点A向左平移两个单位,再向上平移 4个单位得到点C.(1)写出点C的坐标,并作出三角形ABC:(2)求三角形ABC的面积.
A(1,0)
C(-1,4)
B(3,2)
(4×2)÷2=4
(2×2)÷2=2
(4×2)÷2=4
4×4=16
4
2
2
2
4
2
解:
1)C(-1,4)
2)ABC的面积=16-4-2-4=6.
【例8】已知A(1,4),B(-4,0),C(2,0),则△ABC的面积是 .
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
利用平面直角坐标系绘制某一区域的各点分布情况的平面图包括以下过程:
(1)建立适当的坐标系,即选择适当的点作为原点,确定x轴、 y轴的正方向; (注重寻找最佳位置)
(2)根据具体问题确定恰当的比例尺,在数轴上标出单位长度;
(3)在坐标平面上画出各点,写出坐标名称。
考点4:用坐标表示地理位置
试卷12页17题(地理位置)48页19题(建立平面直角坐标系
试卷12页16题(到数轴的距离加面积)
(30页16题较简单可作为作业)
试卷52页19题(重点讲第二小题)
挑战试卷12页18题(不规则图形)
感谢您的聆听
Thank you for listening
