冀教版数学七年级下册 7.4 平行线的性质课件(共13张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 7.4 平行线的性质课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 08:33:03 | ||
图片预览





文档简介
(共13张PPT)
平行线的性质
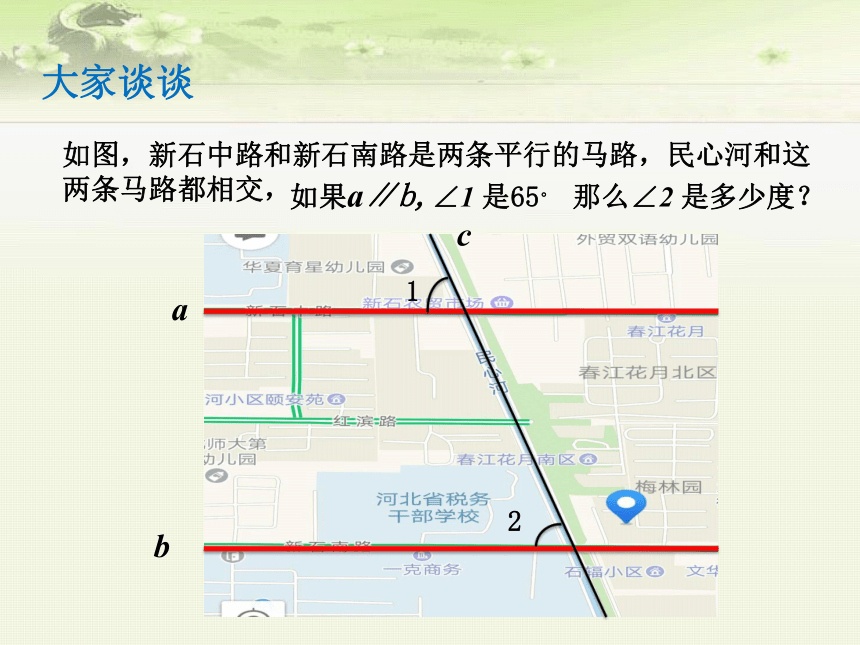
如图,新石中路和新石南路是两条平行的马路,民心河和这两条马路都相交,
大家谈谈
b
a
如果a∥b,∠1 是65。 那么∠2 是多少度?
c
1
2
c
a
b
1
2
已知直线a∥b,且被直线c所截
猜想同位角∠1和∠2的大小有什么关系,并验证你的猜想.
观察猜想
图中其它的同位角是否也相等呢?
观察猜想
已知直线a∥b,且被直线c所截
请你画一条直线 d,使它和 a , b 都相交,度量其中任意一对同位角,看其大小有什么关系.
c
a
b
得出结论
两条平行线被第三条直线所截,同位角相等.
简称为:
平行线的性质定理
符号语言:
∵a∥b(已知)
两直线平行,同位角相等.
∴∠1=∠2(两直线平行,同位角相等)
实验探究
如图,已知直线a∥b,且被直线c所截
请大家观察图上的内错角和同旁内角,并猜想它们又有什么样的数量关系?为什么?
c
a
b
已知:如图,直线a∥b,且被直线c所截,
求证:∠1=∠2
理由:∵ a∥b ( )
b
1
2
a
c
学会说理
两条平行线被第三条直线所截,内错角相等.
两直线平行,内错角相等.
符号语言:
理由:
学会说理
两条平行线被第三条直线所截,同旁内角互补.
两直线平行,同旁内角互补.
已知:如图,直线a∥b ,且被直线c所截,求证:∠1+∠2=180°
b
1
2
a
c
符号语言:
平行线的判定和性质有什么联系和区别?
条件
结论
判定 同位角相等
两直线平行
内错角相等 同旁内角互补 性质 两直线平行
同位角相等
内错角相等
同旁内角互补
对比分析
1.已知:如图,a∥b,c∥d, ∠1=73°. 求
∠2和∠3的度数.
解:∵ a∥b (已知)
∴ ∠1=∠2 (两直线平行,
内错角相等)
∵ ∠1=73°(已知)
∴ ∠2=73°(等量代换)
∵ c∥d (已知)
∴ ∠2+∠3=180 ° (两直线平行, 同旁内角互补)
∴ ∠3=180°—∠2 (等式的性质)
∴ ∠3=180°—73°=107°(等量代换)
有理有据
2.请你写出命题“如图,如果∠B=∠C,那么∠A+∠1=180°”的说理过程.
有理有据
知识与方法
1.本节课我们经历了一个怎样的探索过程?
观察猜想
实验探究
得出结论
解决问题
反思提高
知识与方法
2.我们学到了哪些知识?
两直线平行, 同位角相等.
两直线平行, 内错角相等.
两直线平行,同旁内角互补.
3. 平行线的性质与判定的联系和区别:
判定
同旁内角互补
内错角相等
同位角相等
两直线平行
性质
反思提高
平行线的性质
如图,新石中路和新石南路是两条平行的马路,民心河和这两条马路都相交,
大家谈谈
b
a
如果a∥b,∠1 是65。 那么∠2 是多少度?
c
1
2
c
a
b
1
2
已知直线a∥b,且被直线c所截
猜想同位角∠1和∠2的大小有什么关系,并验证你的猜想.
观察猜想
图中其它的同位角是否也相等呢?
观察猜想
已知直线a∥b,且被直线c所截
请你画一条直线 d,使它和 a , b 都相交,度量其中任意一对同位角,看其大小有什么关系.
c
a
b
得出结论
两条平行线被第三条直线所截,同位角相等.
简称为:
平行线的性质定理
符号语言:
∵a∥b(已知)
两直线平行,同位角相等.
∴∠1=∠2(两直线平行,同位角相等)
实验探究
如图,已知直线a∥b,且被直线c所截
请大家观察图上的内错角和同旁内角,并猜想它们又有什么样的数量关系?为什么?
c
a
b
已知:如图,直线a∥b,且被直线c所截,
求证:∠1=∠2
理由:∵ a∥b ( )
b
1
2
a
c
学会说理
两条平行线被第三条直线所截,内错角相等.
两直线平行,内错角相等.
符号语言:
理由:
学会说理
两条平行线被第三条直线所截,同旁内角互补.
两直线平行,同旁内角互补.
已知:如图,直线a∥b ,且被直线c所截,求证:∠1+∠2=180°
b
1
2
a
c
符号语言:
平行线的判定和性质有什么联系和区别?
条件
结论
判定 同位角相等
两直线平行
内错角相等 同旁内角互补 性质 两直线平行
同位角相等
内错角相等
同旁内角互补
对比分析
1.已知:如图,a∥b,c∥d, ∠1=73°. 求
∠2和∠3的度数.
解:∵ a∥b (已知)
∴ ∠1=∠2 (两直线平行,
内错角相等)
∵ ∠1=73°(已知)
∴ ∠2=73°(等量代换)
∵ c∥d (已知)
∴ ∠2+∠3=180 ° (两直线平行, 同旁内角互补)
∴ ∠3=180°—∠2 (等式的性质)
∴ ∠3=180°—73°=107°(等量代换)
有理有据
2.请你写出命题“如图,如果∠B=∠C,那么∠A+∠1=180°”的说理过程.
有理有据
知识与方法
1.本节课我们经历了一个怎样的探索过程?
观察猜想
实验探究
得出结论
解决问题
反思提高
知识与方法
2.我们学到了哪些知识?
两直线平行, 同位角相等.
两直线平行, 内错角相等.
两直线平行,同旁内角互补.
3. 平行线的性质与判定的联系和区别:
判定
同旁内角互补
内错角相等
同位角相等
两直线平行
性质
反思提高
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
