冀教版数学七年级下册 7.2 相交线 (2)课件(共23张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 7.2 相交线 (2)课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 261.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 08:40:04 | ||
图片预览







文档简介
(共23张PPT)
相交线
知识与技能
对顶角的概念、性质,并能利用它进行简单的推理和计算;
通过变式图形的识图训练,提高识图能力。
理解同位角、内错角同旁内角特点,能准确识别同位角、内错角、同旁内角,
过程与方法
经历实际操作,通过观察讨论等活动,能在具体的情境中认识对顶角、邻补角。
理解三线八角中第三条线,准确找出第三条线。
情感态度价值观
认识几何图形的位置美。通过对顶角性质的推理过程,提高推理和逻辑思维能力;培养抽象能力
如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点。
直线AB、CD相交于点O
问题:两条相交直线.形成的小于平角的
角有几个
请你画出任意两条相交直线,用量角器量一量4个角的度数,看看这四个角有什么关系
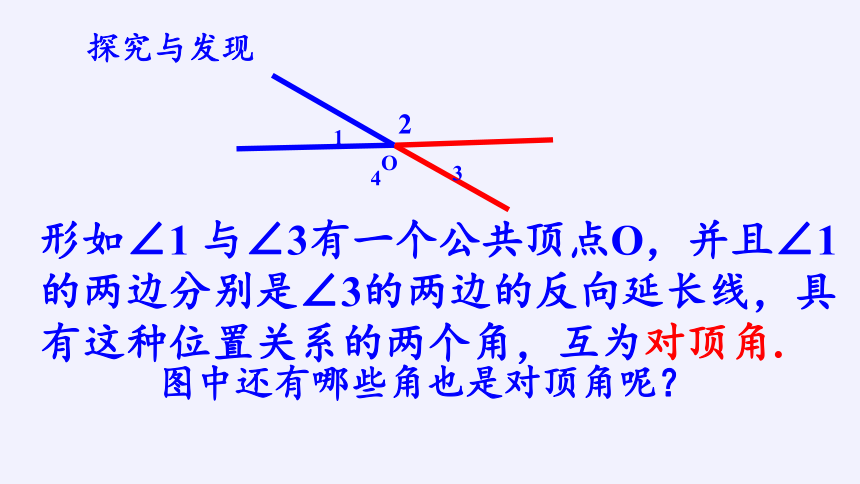
探究与发现
1
2
3
4
O
形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
图中还有哪些角也是对顶角呢?
注意以下两点:(1)辨认对顶角的要领:一看是不是两条直线相交所成的角,哪里有相交直线,哪里就有对顶角,反过来,哪里有对顶角,哪里就有相交线;二看是不是有公共顶点;三看是不是没有公共边,符合这三个条件时,才能确定这两个角是对顶角,只具备一个或两个条件都不行。(2)对顶角是成对存在的,它们是互为对顶角,如∠1是∠3的对顶角,同时,∠3是∠1的对顶角,也常说∠1和∠3是对顶角。
O
A
B
C
D
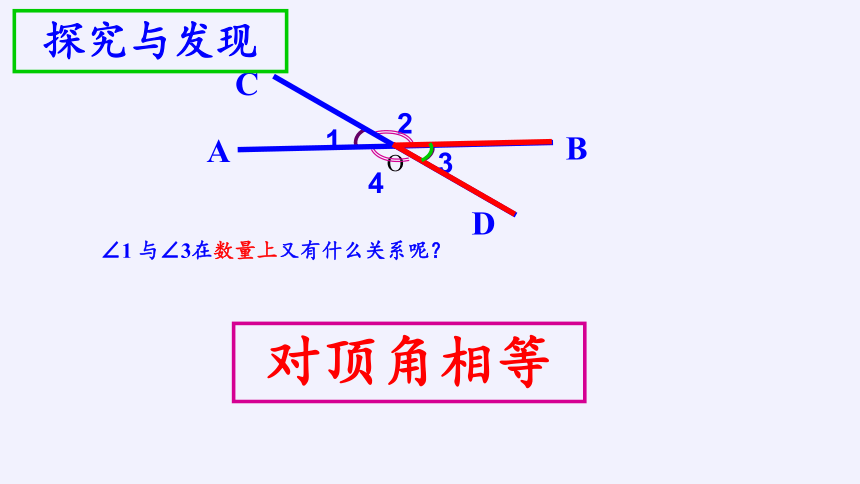
探究与发现
对顶角相等
4
3
2
1
∠1 与∠3在数量上又有什么关系呢?
对顶角的性质:
对顶角相等.
O
A
B
C
D
)
(
1
3
4
2
)
(
为什么
请对真命题用说理方法进行说明
∵直线AB与CD相交于O点,
∴∠1+∠2=180°, ∠3+∠2=180°
∴∠1=∠3
同理可得:∠2=∠4当然还可用量角器、重叠方法验证
7
8
5
6
A
B
4
1
3
2
C
D
E
F
两条直线AB和CD被第三条直线EF所截成的小于平角的角共有几个?----(三线八角)
直线EF---截线(第三条直线)
直线AB、CD----被截直线
5
1
7
8
5
4
1
3
2
6
2
6
7
3
5
1
在第三条直线同侧,在另两直线上方(相同位置)
观察∠1和∠5两角:
5
1
同位角
观察∠1和∠5两角:
分别在截线的左侧,在被截直线的下方
5
1
7
8
5
4
1
3
2
6
2
6
7
3
8
4
图中的同位角除∠1和∠5外,还有……
5
1
7
8
5
4
1
3
2
6
2
6
7
3
各有一边在同一直线上
5
3
观察∠3和∠5两角:
内错角
5
3
观察∠3和∠5两角:
夹在两被截直线 ,分别在截线两侧( ) 上图中还有没有这种角
5
1
7
8
5
4
1
3
2
6
2
6
7
3
3
6
观察∠3和∠6:
同旁内角
3
6
观察∠3和∠6:
在截线同旁,夹在两被截直线内
做游戏:
请同学们分别用双手的大拇指,食指各组成一个角,两食指相对成一条线,保持在同一平面内,分别进行尝试,看可以组成哪些角。
达标测试
一、判断题
1、有公共顶点且相等的两个角是对顶角。( )
2、两条直线相交,有两组对顶角。 ( )
3、两条直线相交所构成的四个角中有一个角是直角,
那么其余的三个角也是直角。 ( )
二、选择题
1、如右图直线AB、CD交于点O,OE为射线,那么( )
A、∠AOC和∠BOE是对顶角;
B、∠COE和∠AOD是对顶角;
C、∠BOC和∠AOD是对顶角;
D、∠AOE和∠DOE是对顶角。
2、如右图中直线AB、CD交于O,
∠AOC=50度,
那么∠AOD=( )度∠BOD=( )度
A
B
C
D
O
看谁最棒!
1
三、下列各图中∠1、∠2是对顶角吗?为什么?
2
1
2
1
2
)
(
(
(
)
)
下列各图中 与 哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
例:如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角?
D
E
C
B
A
2
4
3
1
形如字母“U”
在两条被截直线同旁,在截线同侧
同旁内角
形如字母“Z”
(或反置)
在两条被截直线之内,在截线两侧(交错)
内错角
形如字母“F”
(或倒置)
在两条被截直线同旁,在截线同侧
同位角
图形结构特征
位 置 特 征
角的名称
课堂小结:
谢 谢
相交线
知识与技能
对顶角的概念、性质,并能利用它进行简单的推理和计算;
通过变式图形的识图训练,提高识图能力。
理解同位角、内错角同旁内角特点,能准确识别同位角、内错角、同旁内角,
过程与方法
经历实际操作,通过观察讨论等活动,能在具体的情境中认识对顶角、邻补角。
理解三线八角中第三条线,准确找出第三条线。
情感态度价值观
认识几何图形的位置美。通过对顶角性质的推理过程,提高推理和逻辑思维能力;培养抽象能力
如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点。
直线AB、CD相交于点O
问题:两条相交直线.形成的小于平角的
角有几个
请你画出任意两条相交直线,用量角器量一量4个角的度数,看看这四个角有什么关系
探究与发现
1
2
3
4
O
形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
图中还有哪些角也是对顶角呢?
注意以下两点:(1)辨认对顶角的要领:一看是不是两条直线相交所成的角,哪里有相交直线,哪里就有对顶角,反过来,哪里有对顶角,哪里就有相交线;二看是不是有公共顶点;三看是不是没有公共边,符合这三个条件时,才能确定这两个角是对顶角,只具备一个或两个条件都不行。(2)对顶角是成对存在的,它们是互为对顶角,如∠1是∠3的对顶角,同时,∠3是∠1的对顶角,也常说∠1和∠3是对顶角。
O
A
B
C
D
探究与发现
对顶角相等
4
3
2
1
∠1 与∠3在数量上又有什么关系呢?
对顶角的性质:
对顶角相等.
O
A
B
C
D
)
(
1
3
4
2
)
(
为什么
请对真命题用说理方法进行说明
∵直线AB与CD相交于O点,
∴∠1+∠2=180°, ∠3+∠2=180°
∴∠1=∠3
同理可得:∠2=∠4当然还可用量角器、重叠方法验证
7
8
5
6
A
B
4
1
3
2
C
D
E
F
两条直线AB和CD被第三条直线EF所截成的小于平角的角共有几个?----(三线八角)
直线EF---截线(第三条直线)
直线AB、CD----被截直线
5
1
7
8
5
4
1
3
2
6
2
6
7
3
5
1
在第三条直线同侧,在另两直线上方(相同位置)
观察∠1和∠5两角:
5
1
同位角
观察∠1和∠5两角:
分别在截线的左侧,在被截直线的下方
5
1
7
8
5
4
1
3
2
6
2
6
7
3
8
4
图中的同位角除∠1和∠5外,还有……
5
1
7
8
5
4
1
3
2
6
2
6
7
3
各有一边在同一直线上
5
3
观察∠3和∠5两角:
内错角
5
3
观察∠3和∠5两角:
夹在两被截直线 ,分别在截线两侧( ) 上图中还有没有这种角
5
1
7
8
5
4
1
3
2
6
2
6
7
3
3
6
观察∠3和∠6:
同旁内角
3
6
观察∠3和∠6:
在截线同旁,夹在两被截直线内
做游戏:
请同学们分别用双手的大拇指,食指各组成一个角,两食指相对成一条线,保持在同一平面内,分别进行尝试,看可以组成哪些角。
达标测试
一、判断题
1、有公共顶点且相等的两个角是对顶角。( )
2、两条直线相交,有两组对顶角。 ( )
3、两条直线相交所构成的四个角中有一个角是直角,
那么其余的三个角也是直角。 ( )
二、选择题
1、如右图直线AB、CD交于点O,OE为射线,那么( )
A、∠AOC和∠BOE是对顶角;
B、∠COE和∠AOD是对顶角;
C、∠BOC和∠AOD是对顶角;
D、∠AOE和∠DOE是对顶角。
2、如右图中直线AB、CD交于O,
∠AOC=50度,
那么∠AOD=( )度∠BOD=( )度
A
B
C
D
O
看谁最棒!
1
三、下列各图中∠1、∠2是对顶角吗?为什么?
2
1
2
1
2
)
(
(
(
)
)
下列各图中 与 哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
例:如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角?
D
E
C
B
A
2
4
3
1
形如字母“U”
在两条被截直线同旁,在截线同侧
同旁内角
形如字母“Z”
(或反置)
在两条被截直线之内,在截线两侧(交错)
内错角
形如字母“F”
(或倒置)
在两条被截直线同旁,在截线同侧
同位角
图形结构特征
位 置 特 征
角的名称
课堂小结:
谢 谢
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
