北京版八年级数学下册《15.5 三角形中位线定理》教学设计
文档属性
| 名称 | 北京版八年级数学下册《15.5 三角形中位线定理》教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 00:00:00 | ||
图片预览

文档简介
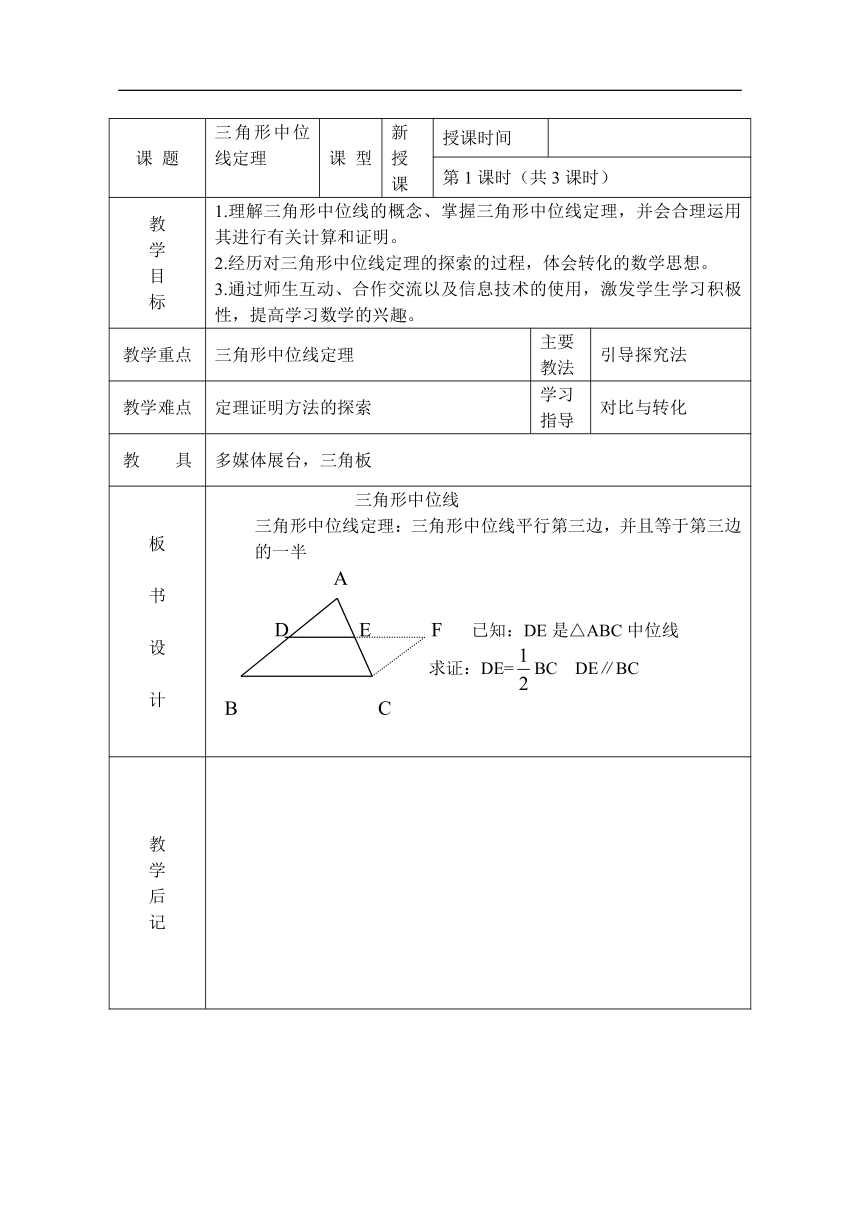
课 题 三角形中位线定理 课 型 新授课 授课时间
第1课时(共3课时)
教 学 目 标 1.理解三角形中位线的概念、掌握三角形中位线定理,并会合理运用其进行有关计算和证明。 2.经历对三角形中位线定理的探索的过程,体会转化的数学思想。 3.通过师生互动、合作交流以及信息技术的使用,激发学生学习积极性,提高学习数学的兴趣。
教学重点 三角形中位线定理 主要 教法 引导探究法
教学难点 定理证明方法的探索 学习 指导 对比与转化
教 具 多媒体展台,三角板
板 书 设 计 三角形中位线 三角形中位线定理:三角形中位线平行第三边,并且等于第三边的一半 A D E F 已知:DE是△ABC中位线 求证:DE=BC DE∥BC B C
教 学 后 记
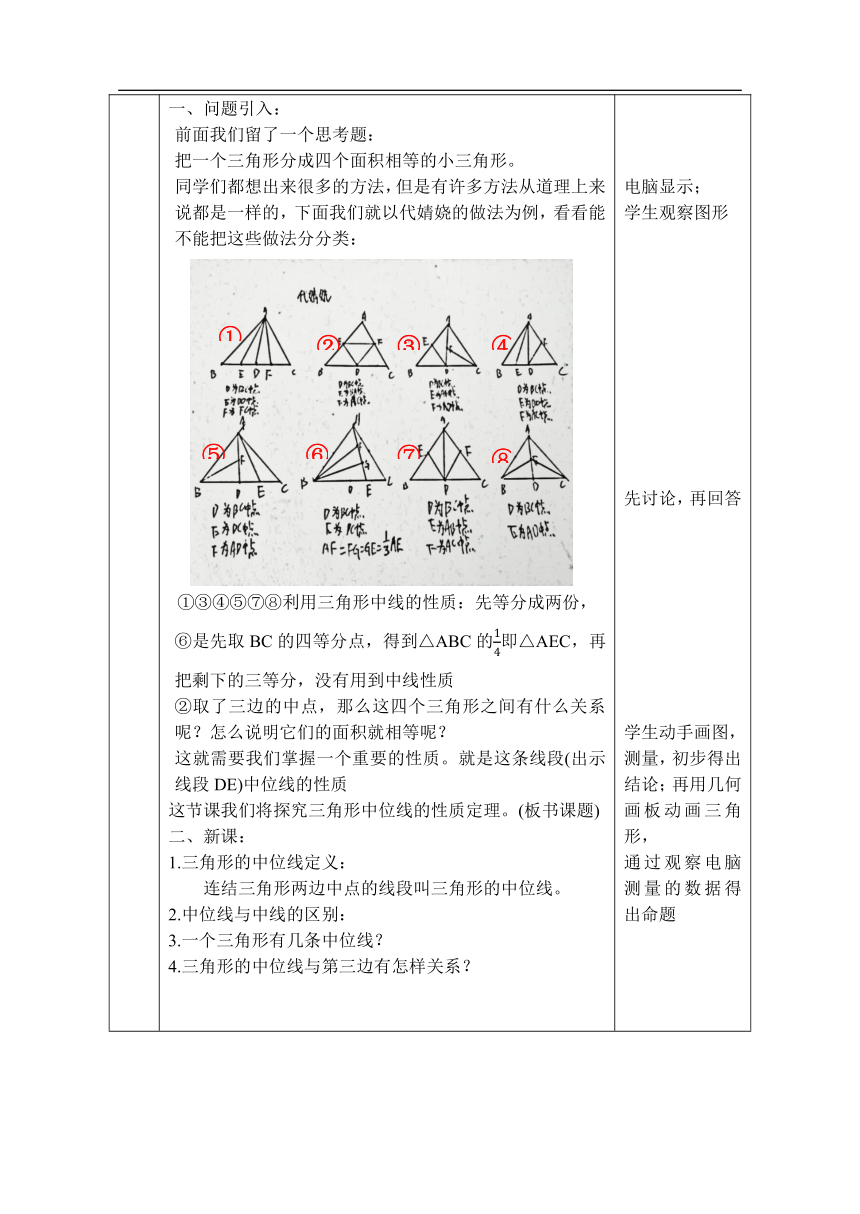
问题引入: 前面我们留了一个思考题: 把一个三角形分成四个面积相等的小三角形。 同学们都想出来很多的方法,但是有许多方法从道理上来说都是一样的,下面我们就以代婧娆的做法为例,看看能不能把这些做法分分类: ①③④⑤⑦⑧利用三角形中线的性质:先等分成两份, ⑥是先取BC的四等分点,得到△ABC的即△AEC,再把剩下的三等分,没有用到中线性质 ②取了三边的中点,那么这四个三角形之间有什么关系呢?怎么说明它们的面积就相等呢? 这就需要我们掌握一个重要的性质。就是这条线段(出示线段DE)中位线的性质 这节课我们将探究三角形中位线的性质定理。(板书课题) 二、新课: 1.三角形的中位线定义: 连结三角形两边中点的线段叫三角形的中位线。 2.中位线与中线的区别: 3.一个三角形有几条中位线? 4.三角形的中位线与第三边有怎样关系? 电脑显示; 学生观察图形 先讨论,再回答 学生动手画图,测量,初步得出结论;再用几何画板动画三角形, 通过观察电脑测量的数据得出命题
教
学 过 程 ︵ 含时间分配 ︶ 教学内容及教师活动 学生活动
命题:三角形的中位线平行于第三边,并且等于第三边的一半。 已知:在△ABC中,DE是△ABC的中位线 求证:DE∥BC,DE=BC。 证明:延长DE到F,使EF=DE,连结CF。 ∵ AE=EC ∠AED=∠CEF DE=EF ∴△AED≌△CEF ∴AD=CF,∠ADE=∠F, ∴AD∥CF。 ∵AD=DB, CF∥DB,且CF=DB, ∴四边形BCFD是平行四边形, ∴DF=BC,DE∥BC ∴DE=DF=BC (引导学生添加其他的辅助线进行证明) 引出定理:三角形的中位线平行于第三边,并且等于第三边的一半。 三、巩固练习: 1.如图1:在△ABC中,DE是中位线. (1)若∠ADE=60°, 则∠B= 度,为什么? (2)若BC=8cm, 则DE= cm,为什么? 2.解决引入中的问题:探究四个三角形之间的关系: 学生小组讨论,说出添加辅助线的方法,并完成证明 口答 小组讨论,并回答
3.例题:如图,D,E,F是△ABC中的AB,AC,BC中点. 求证:AF与DE互相平分. 四、课堂小结: 1.三角形中位线及中位线定理 2.应用:证明线段平行;线段之半、之倍问题 3.方法:见中点,想旋转,构造中点8字形 五、作业: 1.必做:导学案82页 2.选做:三角形中位线定理的其他证明方法
第1课时(共3课时)
教 学 目 标 1.理解三角形中位线的概念、掌握三角形中位线定理,并会合理运用其进行有关计算和证明。 2.经历对三角形中位线定理的探索的过程,体会转化的数学思想。 3.通过师生互动、合作交流以及信息技术的使用,激发学生学习积极性,提高学习数学的兴趣。
教学重点 三角形中位线定理 主要 教法 引导探究法
教学难点 定理证明方法的探索 学习 指导 对比与转化
教 具 多媒体展台,三角板
板 书 设 计 三角形中位线 三角形中位线定理:三角形中位线平行第三边,并且等于第三边的一半 A D E F 已知:DE是△ABC中位线 求证:DE=BC DE∥BC B C
教 学 后 记
问题引入: 前面我们留了一个思考题: 把一个三角形分成四个面积相等的小三角形。 同学们都想出来很多的方法,但是有许多方法从道理上来说都是一样的,下面我们就以代婧娆的做法为例,看看能不能把这些做法分分类: ①③④⑤⑦⑧利用三角形中线的性质:先等分成两份, ⑥是先取BC的四等分点,得到△ABC的即△AEC,再把剩下的三等分,没有用到中线性质 ②取了三边的中点,那么这四个三角形之间有什么关系呢?怎么说明它们的面积就相等呢? 这就需要我们掌握一个重要的性质。就是这条线段(出示线段DE)中位线的性质 这节课我们将探究三角形中位线的性质定理。(板书课题) 二、新课: 1.三角形的中位线定义: 连结三角形两边中点的线段叫三角形的中位线。 2.中位线与中线的区别: 3.一个三角形有几条中位线? 4.三角形的中位线与第三边有怎样关系? 电脑显示; 学生观察图形 先讨论,再回答 学生动手画图,测量,初步得出结论;再用几何画板动画三角形, 通过观察电脑测量的数据得出命题
教
学 过 程 ︵ 含时间分配 ︶ 教学内容及教师活动 学生活动
命题:三角形的中位线平行于第三边,并且等于第三边的一半。 已知:在△ABC中,DE是△ABC的中位线 求证:DE∥BC,DE=BC。 证明:延长DE到F,使EF=DE,连结CF。 ∵ AE=EC ∠AED=∠CEF DE=EF ∴△AED≌△CEF ∴AD=CF,∠ADE=∠F, ∴AD∥CF。 ∵AD=DB, CF∥DB,且CF=DB, ∴四边形BCFD是平行四边形, ∴DF=BC,DE∥BC ∴DE=DF=BC (引导学生添加其他的辅助线进行证明) 引出定理:三角形的中位线平行于第三边,并且等于第三边的一半。 三、巩固练习: 1.如图1:在△ABC中,DE是中位线. (1)若∠ADE=60°, 则∠B= 度,为什么? (2)若BC=8cm, 则DE= cm,为什么? 2.解决引入中的问题:探究四个三角形之间的关系: 学生小组讨论,说出添加辅助线的方法,并完成证明 口答 小组讨论,并回答
3.例题:如图,D,E,F是△ABC中的AB,AC,BC中点. 求证:AF与DE互相平分. 四、课堂小结: 1.三角形中位线及中位线定理 2.应用:证明线段平行;线段之半、之倍问题 3.方法:见中点,想旋转,构造中点8字形 五、作业: 1.必做:导学案82页 2.选做:三角形中位线定理的其他证明方法
同课章节目录
