北京版八年级数学下册15.3《平行四边形性质(1) 》教学设计
文档属性
| 名称 | 北京版八年级数学下册15.3《平行四边形性质(1) 》教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 11:29:12 | ||
图片预览

文档简介
课题:平行四边形性质(1) 教学案
【教学目标】
(1)理解平行四边形的定义及有关概念。
(2)能根据定义探索并掌握平行四边形的对边相等、对角相等的性质。
(3)能运用平行四边形性质解决简单实际问题,体会用代数方法解几何问题的数学思想方法。
【教学重点】
平行四边形的概念和性质的认识和掌握。
【教学难点】
如何添加辅助线将平行四边形问题 ,转化为三角形问题解决的思想方法。
【教学过程】
一、创设情境,导入课题
观察下图中的伸缩门、竹篱笆格子和汽车的防护链,想一想它们是什么几何图形的形象?
你们还记得平行四边形的定义吗?
二、实践探究,讲授新课
(一)复习巩固,有关概念
1、平行四边形的概念:两组对边分别平行的四边形叫做平行四边形。
在平行四边形ABCD中,
记作: 读作:平行四边形ABCD
对边:AB与CD, AD与BC
对角:∠A和∠C,∠B和∠D.
2、平行四边形定义具有双重性:
(2)合作交流,探求新知
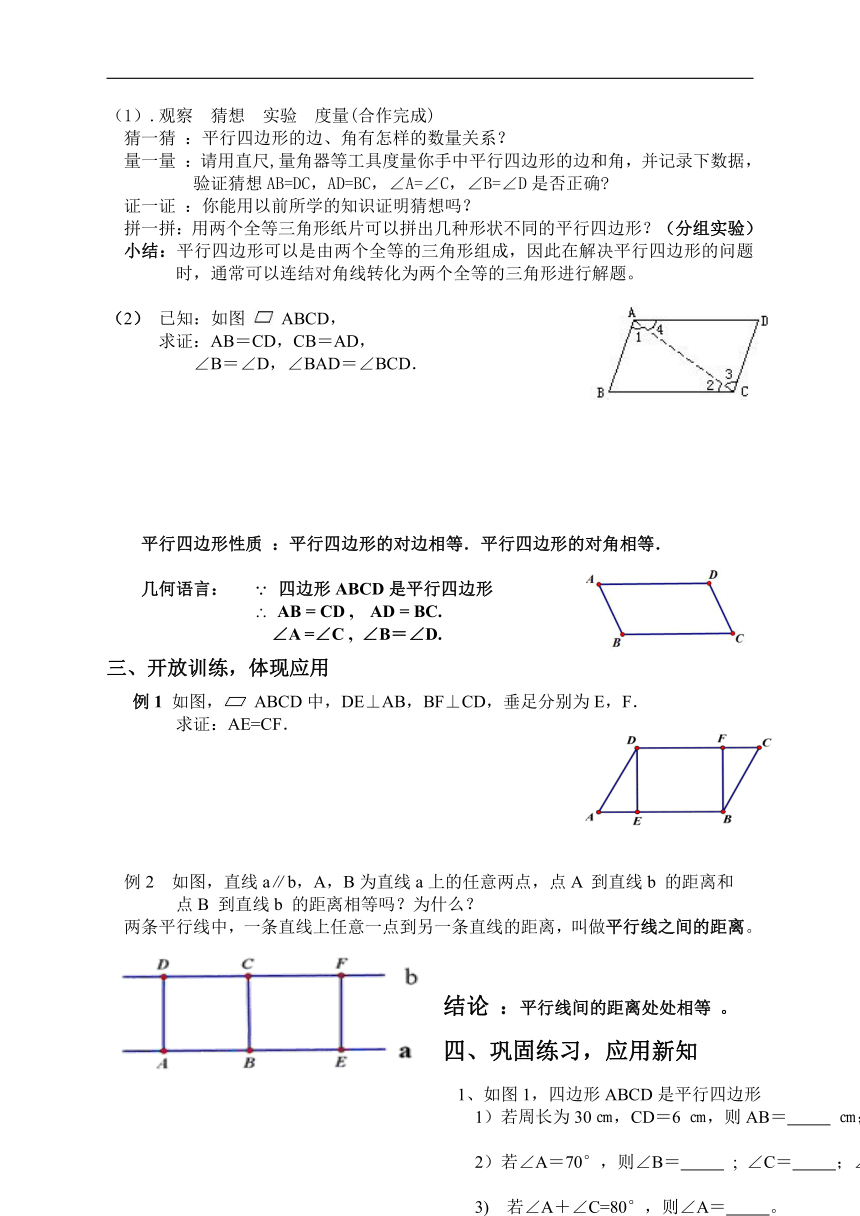
(1).观察 猜想 实验 度量(合作完成)
猜一猜 :平行四边形的边、角有怎样的数量关系?
量一量 :请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
证一证 :你能用以前所学的知识证明猜想吗?
拼一拼:用两个全等三角形纸片可以拼出几种形状不同的平行四边形?(分组实验)
小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
(2) 已知:如图 ABCD,
求证:AB=CD,CB=AD,
∠B=∠D,∠BAD=∠BCD.
平行四边形性质 :平行四边形的对边相等.平行四边形的对角相等.
几何语言: 四边形ABCD是平行四边形
AB = CD , AD = BC.
∠A =∠C , ∠B=∠D.
三、开放训练,体现应用
例1 如图, ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
求证:AE=CF.
例2 如图,直线a∥b,A,B为直线a上的任意两点,点A 到直线b 的距离和
点B 到直线b 的距离相等吗?为什么?
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做平行线之间的距离。
结论 :平行线间的距离处处相等 。
四、巩固练习,应用新知
2、如图2,直线 a // b ,点C、D在直线 a上,点A、B在直线 b上, ABC 和
ABD的面积相等吗?为什么?
3、如图3 , ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A .6cm B. 4cm C. 8cm D. 12cm
4、在 ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A. 1:2:3:4 B.1:2:2:1 C.1:1:2:2 D.2:1:2:1
5、如图2,直线 a //b ,点C、D在直线a上,点A、B在直线b上,BC、AD交于点E,则图 中面积相等的三角形有( )对。
A. 1 B. 2 C. 3 D. 4
图1 图2 图3
五、反思小结,持续发展
巩 固 练 习
A 级
1、如图DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个
2、已知在 ABCD中,
①若∠A=50°,则∠B=___;∠C=___;∠D=___。
②若∠A+∠C=200°,则∠A=____;∠D=___ 。
3、在 ABCD中,AB=3cm,BC=8cm 则 ABCD的周长是 cm
4、已知在 ABCD中,AB=4cm, ABCD的周长为20cm,则
BC=____cm.
B 级
5、 ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD 的两邻边长分别为多少?
6、 ABCD的周长为30cm,AB比BC长5cm,则AB = ______cm,
CD =_____ cm.
7、△ABC是等腰三角形,AB=AC, P是底边BC上一动点,PE∥AB,
PF∥AC,点E,F分别在AC,AB上.
求证:PE+PF=AB
D
A
ABCD
C
B
A
D
C
B
1、如图1,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝;BC= ㎝;AD= ㎝.
2)若∠A=70°,则∠B= ; ∠C= ;∠D= 。
3) 若∠A+∠C=80°,则∠A= 。
1、平行四边形定义:两组对边分别平行的四边形是平行四边形。
2、平行四边形的性质:
① 边的性质:对边平行且相等。 ② 角的性质:对角相等。
3、平行线的性质:平行线间的距离处处相等。
4、平行四边形中常用辅助线的添法:连对角线或过顶点作对边的垂线
【教学目标】
(1)理解平行四边形的定义及有关概念。
(2)能根据定义探索并掌握平行四边形的对边相等、对角相等的性质。
(3)能运用平行四边形性质解决简单实际问题,体会用代数方法解几何问题的数学思想方法。
【教学重点】
平行四边形的概念和性质的认识和掌握。
【教学难点】
如何添加辅助线将平行四边形问题 ,转化为三角形问题解决的思想方法。
【教学过程】
一、创设情境,导入课题
观察下图中的伸缩门、竹篱笆格子和汽车的防护链,想一想它们是什么几何图形的形象?
你们还记得平行四边形的定义吗?
二、实践探究,讲授新课
(一)复习巩固,有关概念
1、平行四边形的概念:两组对边分别平行的四边形叫做平行四边形。
在平行四边形ABCD中,
记作: 读作:平行四边形ABCD
对边:AB与CD, AD与BC
对角:∠A和∠C,∠B和∠D.
2、平行四边形定义具有双重性:
(2)合作交流,探求新知
(1).观察 猜想 实验 度量(合作完成)
猜一猜 :平行四边形的边、角有怎样的数量关系?
量一量 :请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
证一证 :你能用以前所学的知识证明猜想吗?
拼一拼:用两个全等三角形纸片可以拼出几种形状不同的平行四边形?(分组实验)
小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
(2) 已知:如图 ABCD,
求证:AB=CD,CB=AD,
∠B=∠D,∠BAD=∠BCD.
平行四边形性质 :平行四边形的对边相等.平行四边形的对角相等.
几何语言: 四边形ABCD是平行四边形
AB = CD , AD = BC.
∠A =∠C , ∠B=∠D.
三、开放训练,体现应用
例1 如图, ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
求证:AE=CF.
例2 如图,直线a∥b,A,B为直线a上的任意两点,点A 到直线b 的距离和
点B 到直线b 的距离相等吗?为什么?
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做平行线之间的距离。
结论 :平行线间的距离处处相等 。
四、巩固练习,应用新知
2、如图2,直线 a // b ,点C、D在直线 a上,点A、B在直线 b上, ABC 和
ABD的面积相等吗?为什么?
3、如图3 , ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A .6cm B. 4cm C. 8cm D. 12cm
4、在 ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A. 1:2:3:4 B.1:2:2:1 C.1:1:2:2 D.2:1:2:1
5、如图2,直线 a //b ,点C、D在直线a上,点A、B在直线b上,BC、AD交于点E,则图 中面积相等的三角形有( )对。
A. 1 B. 2 C. 3 D. 4
图1 图2 图3
五、反思小结,持续发展
巩 固 练 习
A 级
1、如图DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个
2、已知在 ABCD中,
①若∠A=50°,则∠B=___;∠C=___;∠D=___。
②若∠A+∠C=200°,则∠A=____;∠D=___ 。
3、在 ABCD中,AB=3cm,BC=8cm 则 ABCD的周长是 cm
4、已知在 ABCD中,AB=4cm, ABCD的周长为20cm,则
BC=____cm.
B 级
5、 ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD 的两邻边长分别为多少?
6、 ABCD的周长为30cm,AB比BC长5cm,则AB = ______cm,
CD =_____ cm.
7、△ABC是等腰三角形,AB=AC, P是底边BC上一动点,PE∥AB,
PF∥AC,点E,F分别在AC,AB上.
求证:PE+PF=AB
D
A
ABCD
C
B
A
D
C
B
1、如图1,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝;BC= ㎝;AD= ㎝.
2)若∠A=70°,则∠B= ; ∠C= ;∠D= 。
3) 若∠A+∠C=80°,则∠A= 。
1、平行四边形定义:两组对边分别平行的四边形是平行四边形。
2、平行四边形的性质:
① 边的性质:对边平行且相等。 ② 角的性质:对角相等。
3、平行线的性质:平行线间的距离处处相等。
4、平行四边形中常用辅助线的添法:连对角线或过顶点作对边的垂线
同课章节目录
