冀教版2020-2021学年河北省邯郸市大名县五年级下期末数学试卷(word版含答案)
文档属性
| 名称 | 冀教版2020-2021学年河北省邯郸市大名县五年级下期末数学试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 385.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 00:00:00 | ||
图片预览




文档简介
2020-2021学年河北省邯郸市大名县五年级(下)期末数学试卷
一、填空。(20分)
1.(4分)5÷4=== (填小数)
2.(2分)在中,当a 时,等于1;当a 时,是真分数。
3.(2分)从3:00到6:00,时针按 方向旋转了 °。
4.(2分)一个正方体的棱长如果扩大到原来的2倍,那么表面积扩大到原来的 倍,体积扩大到原来的 倍。
5.(2分)24和48的最大公因数是 ,最小公倍数是 .
6.(4分)
7000立方厘米= 立方分米 2立方米= 立方分米
4000立方分米= 升 3升= 毫升
7.(1分)四支球队要进行比赛,每2支球队都要进行一场比赛,一共要进行 场比赛。
8.(3分)一个长方体纸箱长6dm,宽和高都是5dm,它的棱长总和是 dm,表面积是 ,体积是 。
二、判断。(对的打“√”,错的打“×”。)(6分)
9.(1分)平行四边形只有一条对称轴. .
10.(1分)5米的与6米的一样长. .
11.(1分)棱长是6厘米的正方体,表面积和体积相等. .
12.(1分)任何自然数(0除外)都有倒数。
13.(1分)有两根1米长的铁丝,第一根用去,第二根用去米,剩下的一样长. .
14.(1分)一个不为零的数除以一个真分数,商大于被除数。
三、选择。(将正确答案的序号填在括号里。)(6分)
15.(1分)下面说法错误的是( )
A.圆有无数条对称轴
B.分母是9的真分数有8个
C.一根绳子对折两次后是米,这根绳子长1米
D.1升=1立方分米
16.(1分)两个数的最大公因数是6,最小公倍数是36,这两个数可能是( )
A.6和36 B.12和36 C.6和18 D.6和12
17.(1分)如果A×=B×=C×,(A、B、C≠0),那么A、B、C中最大的是( )
A.A B.B C.C D.无法确定
18.(1分)一根铁丝可以做成长16cm,宽14cm,高6cm的长方体,如果用它做成一个正方体,正方体的棱长是( )cm。
A.8 B.10 C.12 D.24
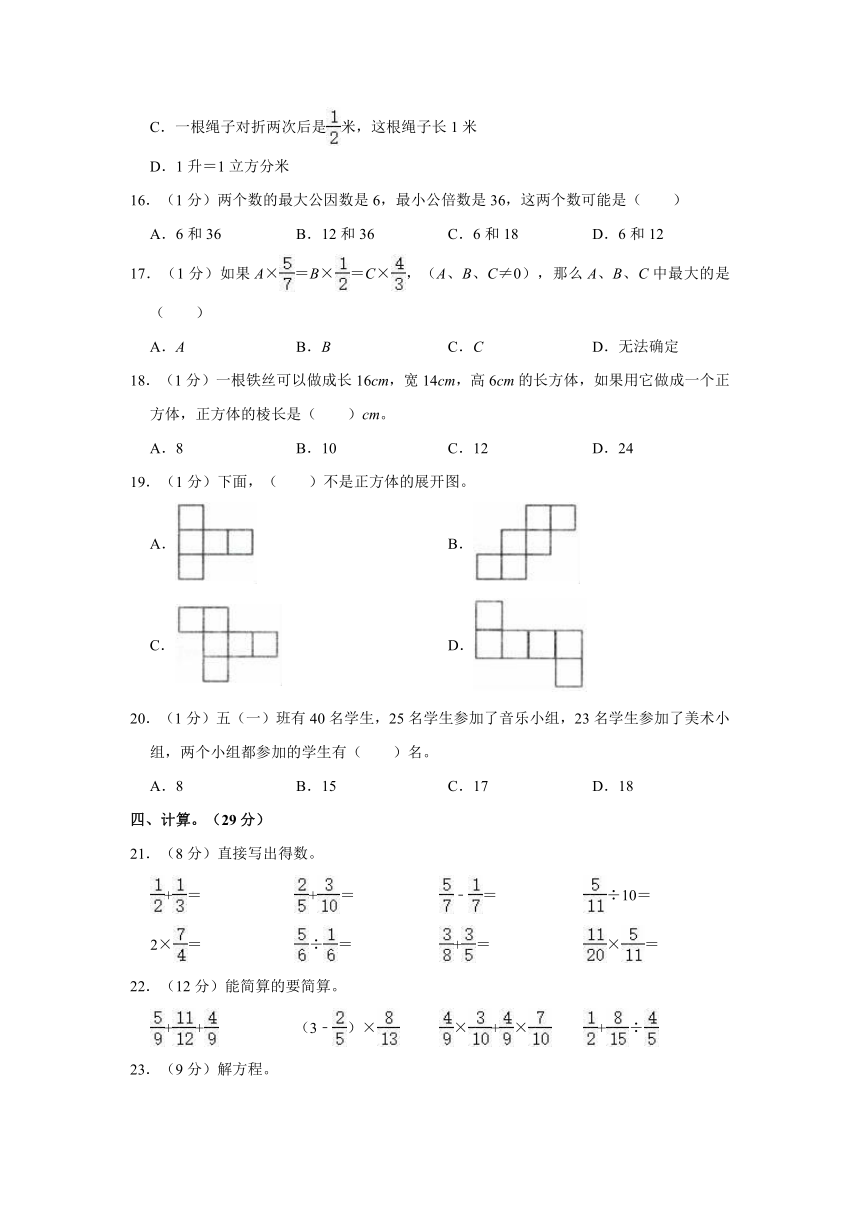
19.(1分)下面,( )不是正方体的展开图。
A. B.
C. D.
20.(1分)五(一)班有40名学生,25名学生参加了音乐小组,23名学生参加了美术小组,两个小组都参加的学生有( )名。
A.8 B.15 C.17 D.18
四、计算。(29分)
21.(8分)直接写出得数。
+= += ﹣= ÷10=
2×= ÷= += ×=
22.(12分)能简算的要简算。
++ (3﹣)× ×+× +÷
23.(9分)解方程。
+x= x= 1﹣x=
五、动手操作。(18分)
24.(6分)按要求画图。
(1)画出将长方形绕A点逆时针旋转90°后的图形。
(2)画出将小旗绕B点逆时针旋转90°后的图形。
(3)画出将平行四边形先左移动3格,再向下移动1格后的图形。
25.(12分)下面是某地家电商场A、B两种品牌电视一年的月销售量统计表。
月份 1 2 3 4 5 6 7 8 9 10 11 12
A 75 80 62 45 55 48 40 42 35 32 36 30
B 30 40 42 45 50 50 52 40 42 50 43 52
(1)请根据表格,完成统计图。
(2)哪种品牌的电视全年销售量高?
(3)哪个月两种电视的销售量最接近?哪个月两种电视的销售量相差最大?
(4)如果你是商场经理,你对新一年的进货安排有什么想法?
六、解决问题。(21分)
26.(4分)用铁皮做一个长10dm的长方体通风管,管道口是一个边长1dm的正方形,做这个通风管至少需要多少平方分米的铁皮?
27.(4分)某修路队计划三周修完一条长400米的小路,第一周修了全长的,第二周修了全长的,第三周要修多少米能按时完工?
28.(4分)把一个长方体铁块从长3.5米,宽2.4米,高1.2米的水缸里取出来,水面下降了0.3米,如果铁块的横截面积是2.1平方米,那么它的长是多少米?
29.(4分)一辆汽车从甲地开往乙地,已经行驶全长的,离乙地还有280千米。甲乙两地相距多少千米?
30.(5分)明明家要给厨房的四周墙壁贴瓷砖,已知厨房的长是3.2米,宽是2米,高是2.4米。如果选用边长40厘米,每块8元的正方形瓷砖,一共需要多少元?
31.智慧乐园:
将一个长方体的高增加2厘米后,就成了一个正方体,表面积比原来增加了40平方厘米,原来长方体的体积是多少立方厘米?
2020-2021学年河北省邯郸市大名县五年级(下)期末数学试卷
参考答案与试题解析
一、填空。(20分)
1.【分析】解答此题的突破口是5÷4,根据分数与除法的关系5÷4=,根据分数的基本性质分子、分母都乘2就是;再求出5÷4的商即可。
【解答】解:5÷4===1.25。
故答案为:1.25。
【点评】此题主要是考查除法、小数、分数之间的关系及分数的基本性质,利用它们之间的关系和性质进行转化即可。
2.【分析】分子小于分母的分数,是真分数;分子大于或等于分母的分数,是假分数,据此解答即可。
【解答】解:在中,当a=5时,等于1;当a>5时,是真分数。
故答案为:=5,>5。
【点评】根据真分数和假分数的定义,解答即可。
3.【分析】钟面上12个数字把钟面平均分成12份,每份所对应的圆周角是360°÷12=30°,即每两个相邻数字间的夹角是30°,即指针从一个数字走到下一个数字时,绕中心轴旋转了30°;据此解答即可。
【解答】解:360°÷12=30°
30°×(6﹣3)
=30°×3
=90°
答:从3:00到6:00,时针按顺时针方向旋转了90°。
故答案为:顺时针,90。
【点评】解答本题关键是弄清指针从一个数字走到另一个相邻的数字,旋转了30°,再弄清顺时针还是逆时针旋转。
4.【分析】根据正方体表面积扩大的倍数是棱长扩大倍数的平方,体积扩大的倍数是棱长扩大倍数的立方求解即可.
【解答】解:一个正方体棱长扩大2倍,则表面积扩大2×2=4倍,体积扩大2×2×2=8倍.
故答案为:4,8.
【点评】考查了正方体的体积,正方体的表面积和正方体棱长的关系,是基础题型,比较简单.
5.【分析】根据倍数关系的最大公因数是较小数,最小公倍数是较大数,24和48是倍数关系,据此解答.
【解答】解;24和48是倍数关系,
所以24和48的最大公因数是24,
最小公倍数是48;
故答案为:24,48.
【点评】本题主要考查求两个数的最大公因数和最小公倍数的方法,注意倍数关系的最大公因数是较小数,最小公倍数是较大数.
6.【分析】低级单位立方厘米化高级单位立方分米除以进率1000;
高级单位立方米化低级单位立方分米乘进率1000;
立方分米与升是等量关系二者互化数值不变;
高级单位升化低级单位毫升乘进率1000。
【解答】解:
7000立方厘米=7立方分米 2立方米=2000立方分米
4000立方分米=4000升 3升=3000毫升
故答案为:7,2000,4000,3000。
【点评】立方米、立方分米(升)、立方厘米(毫升)相邻单位之间的进率是1000,由高级单位化低级单位乘进率,反之除以进率。
7.【分析】每两个队之间赛一场,那么每个队要赛3场,一共是4×3=12(场),但是两队比赛是同一场比赛,所以12场比赛就多算了一倍,再除以2即可。
【解答】解:4×(4﹣1)÷2
=4×3÷2
=6(场)
答:一共要进行6场比赛。
故答案为:6。
【点评】本题属于握手问题,可利用握手问题的公式求解:握手次数=人数×(人数﹣1)÷2进行求解。
8.【分析】根据长方体棱长总和公式:棱长=(长+宽+高)×4,表面积公式:表面积=(长×宽+长×高+宽×高)×2,体积公式:体积=长×宽×高,代入数字即可求解。
【解答】解:棱长总和:(6+5+5)×4
=16×4
=64(分米)
表面积:(6×5+6×5+5×5)×2
=(30+30+25)×2
=85×2
=170(平方分米)
体积:6×5×5
=30×5
=150(立方分米)
答:它的棱长总和是64dm,表面积是170平方分米,体积是150立方分米。
故答案为:64;170平方分米;150立方分米。
【点评】此题主要考查长方体的棱长总和公式,表面积公式、体积公式的运用,关键是要熟记公式。
二、判断。(对的打“√”,错的打“×”。)(6分)
9.【分析】根据轴对称图形的含义:如果一个图形沿一条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;因为平行四边形不是轴对称图形,所以没有对称轴,进而判断即可.
【解答】解:根据轴对称图形的含义可知:平行四边形不是轴对称图形,所以没有对称轴.
故答案为:×.
【点评】判断轴对称的关键是寻找对称轴,两边图形对折后可完全重合.
10.【分析】分别把5米和6米看作单位“1”,根据一个数乘分数的意义,用乘法分别求出5米的是多少米、6米的是多少米,然后进行比较即可.
【解答】解:5×(米)
6×(米)
米
所以原题说法错误;
故答案为:×.
【点评】此题考查的目的是理解掌握一个数乘分数的意义及应用,以及分数大小比较的方法.
11.【分析】正方体的表面积和体积单位不相同,没法比较它们的大小,由此就解决即可.
【解答】解:因为正方体的表面积和体积单位不相同,没法比较它们的大小,
所以原题说法是错误的.
故答案为:×.
【点评】比较两个数的大小必须是统一单位下,面积和体积的单位不同,没法比较.
12.【分析】倒数的意义:乘积是1的两个数互为倒数。
【解答】解:根据倒数的定义可知:0和任何数相乘都得0,所以0没有倒数,其它的自然数都有倒数,原题说法正确。
故答案为:√。
【点评】要熟练掌握求倒数的方法:求一个分数的倒数,把这个分数分子和分母互换位置,求小数的倒数时,要先把小数化成分数。
13.【分析】把第一根的原来的长度看成单位“1”,那么剩下的长度就是原来的(1﹣),用原来的长度乘上这个分率就是剩下的长度;
用第二个原来的长度减去米就是第二根剩下的长度;比较两根剩下的长度即可判断.
【解答】解:1﹣=(米)
1×(1﹣)
=1×
=(米)
两根剩下的长度都是米,所以剩下的长度一样.
故答案为:√.
【点评】此题重在区分分数在具体的题目中的区别:在具体的题目中,带单位是一个具体的数,不带单位是把某一个数量看单位“1”,是它的几分之几.
14.【分析】因为真分数小于1,一个不为零的数除以一个真分数,即除以一个小于1的数,商一定会比原数小。由此解答即可。
【解答】解:因为真分数小于1,一个不为零的数除以一个真分数,即除以一个小于1的数,所以商一定会比原数小。
故答案为:√。
【点评】此题考查商的变化规律。
三、选择。(将正确答案的序号填在括号里。)(6分)
15.【分析】圆有无数条对称轴,每条直径所在的直线,都是它的对称轴;
分母是9的真分数的分子可以是1、2、3、4、5、6、7、8共8个;
把这根绳子的长度看作单位“1”,对折两次后,长度是这根绳子长度的,根据分数除法的意义,即可求出这根绳子的长度;
根据升与立方分米的关系,1升=1立方分米。
【解答】解:圆有无数条对称轴。A说法正确;
分母是9的真分数有:、、、、、、、共8个。B说法正确;
÷=2(米)
一根绳子对折两次后是米,这根绳子长2米。C说法错误;
1升=1立方分米。D说法正确。
故选:C。
【点评】此题考查的知识点:圆的特征及轴对称图形的意义;真分数的意义;分数除法的意义及应用;体积(容积)单位间的进率。
16.【分析】根据为倍数关系的两个数的最大公因数是较小的数,最小公倍数是较大的数,分别求出四个选项中两个数的最大公因数和最小公倍数即可选择。
【解答】解:A.36是6的倍数,所以6和36的最大公因数是6,最小公倍数是36;
B.36是12的倍数,所以12和36的最大公因数是12,最小公倍数是36;
C.18是6的倍数,所以6和18的最大公因数是6,最小公倍数是18;
D.12是6的倍数,所以6和12的最大因数是6,最小公倍数是12。
所以这两个数可能是6和36。
故选:A。
【点评】熟练掌握为倍数关系的两个数的最大公因数是较小的数,最小公倍数是较大的数是解题的关键。
17.【分析】设A×=B×=C×=a(a≠0),再用a分别表示出A、B、C,即可比较出A、B、C的大小。
【解答】解:设A×=B×=C×=a(a≠0),
则A×=a,A=;
B×=a,B=2a;
C×=a,C=a;
2a>>a,
所以B>A>C,最大的是B。
故选:B。
【点评】本题可通过用一个中间数a表示出A、B、C的方法来比较A、B、的大小。
18.【分析】根据长方体的棱长总和=(长+宽+高)×4,求出这根铁丝的长度,然后用这根铁丝的长度除以12即可求出正方体的棱长。
【解答】解:(16+14+6)×4÷12
=36×4÷12
=144÷12
=12(厘米)
答:正方体的棱长是12厘米。
故选:C。
【点评】此题主要考查长方体、正方体棱长总和公式的灵活运用,关键是熟记公式。
19.【分析】根据正方体展开图的11种特征,图A不属于正方体展开图;图B属于正方体展开图的“2﹣2﹣2”结构;图C属于正方体展开图的“1﹣3﹣2”结构;图D属于正方体展开图的“1﹣4﹣1”结构。
【解答】解:不是正方体的展开图。
故选:A。
【点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
20.【分析】因为两个小组都参加的学生是参加音乐小组和美术小组的学生的重叠部分,所以根据容斥原理列式为:25+23﹣40=8(名);据此解答。
【解答】解:25+23﹣40
=48﹣40
=8(名)
答:两个小组都参加的学生有8名。
故选:A。
【点评】本题考查了容斥原理,关键是理解40人包括三部分的人数,知识点是:总人数=(A+B)﹣既A又B。
四、计算。(29分)
21.【分析】根据分数加减乘除法的计算方法求解即可。
【解答】解:
+= += ﹣= ÷10=
2×= ÷=5 += ×=
【点评】本题考查了简单的分数计算,计算时要细心,注意把结果化成最简分数。
22.【分析】(1)根据加法交换律进行计算;
(2)先算小括号里面的减法,再算括号外面的乘法;
(3)根据乘法分配律进行计算;
(4)先算除法,再算加法。
【解答】解:(1)++
=++
=1+
=1
(2)(3﹣)×
=×
=
(3)×+×
=×(+)
=×1
=
(4)+÷
=+
=
【点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
23.【分析】(1)根据等式的性质,方程两边同时减去求解;
(2)根据等式的性质,方程两边同时除以求解;
(3)根据等式的性质,方程两边同时加上x,再两边同时减去求解。
【解答】解:(1)+x=
+x﹣=﹣
x=
(2)x=
x÷=÷
x=
(3)1﹣x=
1﹣x+x=+x
1=+x
1﹣=+x﹣
x=
【点评】此题考查了学生根据等式的性质解方程的能力,注意等号对齐。
五、动手操作。(18分)
24.【分析】(1)(2)根据旋转的意义,找出图中长方形、小旗的关键处,再画出按逆时针方向旋转90度后的形状即可。
(3)根据平移图形的特征,把平行四边形C的四个顶点分别向左平移3格,再向下平移1格,再首尾连接各点,即可得到平行四边形C左移动3格,再向下移动1格后的图形。
【解答】解:如图;
。
【点评】本题考查了图形的旋转变化、平移变化,学生主要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错。
25.【分析】(1)根据统计表中A品牌的数据在统计图中描点,用实线连线,根据统计表中B品牌的数据在统计图中描点,用虚线连线;
(2)分别计算出两种品牌电视的全年总销售,再进行大小比较;
(3)6月份两种电视在统计图中垂直位置最近,所以6月份两种电视销量最接近;1月份两种电视在统计图中垂直位置最远,所以1月份两种电视销量相差最大;
(4)从图中可以看出A品牌的销量呈下降趋势;B品牌的销量呈上升趋势,所以进电视时,要多进些B品牌。(答案不唯一)
【解答】解:(1)折线统计图如下:
(2)75+80+62+45+55+48+40+42+35+32+36+30=580(台)
30+40+42+45+50+50+52+40+42+50+43+52=536(台)
580>536
答:A品牌电视全年总销最高。
(3)6月份两种电视销量最接近,1月份两种电视销量相差最大。
(4)从图中可以看出A品牌的销量呈下降趋势;B品牌的销量呈上升趋势,所以进电视时,要多进些B品牌。(答案不唯一)
【点评】本题考查根据统计表中数据填补复式折线统计图,然后再根据统计图中的信息解决问题。
六、解决问题。(21分)
26.【分析】根据底面周长乘以通风管的长度就是通风管的表面积,代入数字即可求解。
【解答】解:1×4×10
=4×10
=40(平方分米)
答:做这个通风管至少需要40平方分米的铁皮。
【点评】通风管只要侧面积,本题运用“底面周长×长度=侧面积”进行计算即可。
27.【分析】根据题意,把整条路的长度看作单位“1”,则用总长度减去前两周修的长度,计算第三周修的长度即可。
【解答】解:400﹣400×﹣400×
=400﹣80﹣150
=170(米)
答:第三周修170米。
【点评】本题主要考查分数四则运算的应用,关键找对单位“1”,利用数量关系做题。
28.【分析】根据题意可知,把铁块从水缸中取出后,下降部分水的体积就等于这个铁块的体积,再根据长方体的体积公式:V=Sh,那么h=V÷S,用铁块的体积除以铁块的底面积就是铁块的长。
【解答】解:3.5×2.4×0.3÷2.1
=8.4×0.3÷2.1
=2.52÷2.1
=1.2(米)
答:那么它的长是1.2米。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
29.【分析】把甲乙两地之间的路程看作单位“1”,已经行驶全长的,那么剩下的路程占全程的(1),根据已知一个数的几分之几是多少,求这个数,用除法解答。
【解答】解:280÷(1)
=
=
=490(千米)
答:甲乙两地相距490千米。
【点评】此题属于基本的分数除法应用题,关键是确定单位“1”,利用基本数量关系解决问题。
30.【分析】因为只有四周墙壁贴瓷砖,所以首先根据长方体的表面积公式:(长×高+宽×高)×2,求出4面墙壁的面积,再根据正方形的面积公式:S=a2,求出每块瓷砖的面积,然后用墙壁的面积除以每块瓷砖的面积求出需要的块数,再根据单价×数量=总价,据此列式解答。
【解答】解:40厘米=0.4米
(3.2×2.4+2×2.4)×2÷(0.4×0.4)×8
=(7.68+4.8)×2÷0.16×8
=12.48×2÷0.16×8
=24.96÷0.16×8
=156×8
=1248(元)
答:一共需要1248元。
【点评】此题主要考查长方体表面积公式在实际生活中的应用,关键是熟记公式。
31.【分析】高增加2厘米,表面积就增加了一个高为2厘米的长方体的侧面积,用40除以这个长方形的高,可得底面周长,再除以4就是原长方体长和宽的长,再根据长方体的体积公式可求出原来长方体的体积;据此解答。
【解答】解:40÷2÷4=5(厘米)
(5﹣2)×5×5
=3×5×5
=75(立方厘米)
答:原来长方体的体积是75立方厘米。
【点评】本题的关键是让学生理解:高增加2厘米,表面积就增加了一个高为2厘米的长方体的侧面积。
一、填空。(20分)
1.(4分)5÷4=== (填小数)
2.(2分)在中,当a 时,等于1;当a 时,是真分数。
3.(2分)从3:00到6:00,时针按 方向旋转了 °。
4.(2分)一个正方体的棱长如果扩大到原来的2倍,那么表面积扩大到原来的 倍,体积扩大到原来的 倍。
5.(2分)24和48的最大公因数是 ,最小公倍数是 .
6.(4分)
7000立方厘米= 立方分米 2立方米= 立方分米
4000立方分米= 升 3升= 毫升
7.(1分)四支球队要进行比赛,每2支球队都要进行一场比赛,一共要进行 场比赛。
8.(3分)一个长方体纸箱长6dm,宽和高都是5dm,它的棱长总和是 dm,表面积是 ,体积是 。
二、判断。(对的打“√”,错的打“×”。)(6分)
9.(1分)平行四边形只有一条对称轴. .
10.(1分)5米的与6米的一样长. .
11.(1分)棱长是6厘米的正方体,表面积和体积相等. .
12.(1分)任何自然数(0除外)都有倒数。
13.(1分)有两根1米长的铁丝,第一根用去,第二根用去米,剩下的一样长. .
14.(1分)一个不为零的数除以一个真分数,商大于被除数。
三、选择。(将正确答案的序号填在括号里。)(6分)
15.(1分)下面说法错误的是( )
A.圆有无数条对称轴
B.分母是9的真分数有8个
C.一根绳子对折两次后是米,这根绳子长1米
D.1升=1立方分米
16.(1分)两个数的最大公因数是6,最小公倍数是36,这两个数可能是( )
A.6和36 B.12和36 C.6和18 D.6和12
17.(1分)如果A×=B×=C×,(A、B、C≠0),那么A、B、C中最大的是( )
A.A B.B C.C D.无法确定
18.(1分)一根铁丝可以做成长16cm,宽14cm,高6cm的长方体,如果用它做成一个正方体,正方体的棱长是( )cm。
A.8 B.10 C.12 D.24
19.(1分)下面,( )不是正方体的展开图。
A. B.
C. D.
20.(1分)五(一)班有40名学生,25名学生参加了音乐小组,23名学生参加了美术小组,两个小组都参加的学生有( )名。
A.8 B.15 C.17 D.18
四、计算。(29分)
21.(8分)直接写出得数。
+= += ﹣= ÷10=
2×= ÷= += ×=
22.(12分)能简算的要简算。
++ (3﹣)× ×+× +÷
23.(9分)解方程。
+x= x= 1﹣x=
五、动手操作。(18分)
24.(6分)按要求画图。
(1)画出将长方形绕A点逆时针旋转90°后的图形。
(2)画出将小旗绕B点逆时针旋转90°后的图形。
(3)画出将平行四边形先左移动3格,再向下移动1格后的图形。
25.(12分)下面是某地家电商场A、B两种品牌电视一年的月销售量统计表。
月份 1 2 3 4 5 6 7 8 9 10 11 12
A 75 80 62 45 55 48 40 42 35 32 36 30
B 30 40 42 45 50 50 52 40 42 50 43 52
(1)请根据表格,完成统计图。
(2)哪种品牌的电视全年销售量高?
(3)哪个月两种电视的销售量最接近?哪个月两种电视的销售量相差最大?
(4)如果你是商场经理,你对新一年的进货安排有什么想法?
六、解决问题。(21分)
26.(4分)用铁皮做一个长10dm的长方体通风管,管道口是一个边长1dm的正方形,做这个通风管至少需要多少平方分米的铁皮?
27.(4分)某修路队计划三周修完一条长400米的小路,第一周修了全长的,第二周修了全长的,第三周要修多少米能按时完工?
28.(4分)把一个长方体铁块从长3.5米,宽2.4米,高1.2米的水缸里取出来,水面下降了0.3米,如果铁块的横截面积是2.1平方米,那么它的长是多少米?
29.(4分)一辆汽车从甲地开往乙地,已经行驶全长的,离乙地还有280千米。甲乙两地相距多少千米?
30.(5分)明明家要给厨房的四周墙壁贴瓷砖,已知厨房的长是3.2米,宽是2米,高是2.4米。如果选用边长40厘米,每块8元的正方形瓷砖,一共需要多少元?
31.智慧乐园:
将一个长方体的高增加2厘米后,就成了一个正方体,表面积比原来增加了40平方厘米,原来长方体的体积是多少立方厘米?
2020-2021学年河北省邯郸市大名县五年级(下)期末数学试卷
参考答案与试题解析
一、填空。(20分)
1.【分析】解答此题的突破口是5÷4,根据分数与除法的关系5÷4=,根据分数的基本性质分子、分母都乘2就是;再求出5÷4的商即可。
【解答】解:5÷4===1.25。
故答案为:1.25。
【点评】此题主要是考查除法、小数、分数之间的关系及分数的基本性质,利用它们之间的关系和性质进行转化即可。
2.【分析】分子小于分母的分数,是真分数;分子大于或等于分母的分数,是假分数,据此解答即可。
【解答】解:在中,当a=5时,等于1;当a>5时,是真分数。
故答案为:=5,>5。
【点评】根据真分数和假分数的定义,解答即可。
3.【分析】钟面上12个数字把钟面平均分成12份,每份所对应的圆周角是360°÷12=30°,即每两个相邻数字间的夹角是30°,即指针从一个数字走到下一个数字时,绕中心轴旋转了30°;据此解答即可。
【解答】解:360°÷12=30°
30°×(6﹣3)
=30°×3
=90°
答:从3:00到6:00,时针按顺时针方向旋转了90°。
故答案为:顺时针,90。
【点评】解答本题关键是弄清指针从一个数字走到另一个相邻的数字,旋转了30°,再弄清顺时针还是逆时针旋转。
4.【分析】根据正方体表面积扩大的倍数是棱长扩大倍数的平方,体积扩大的倍数是棱长扩大倍数的立方求解即可.
【解答】解:一个正方体棱长扩大2倍,则表面积扩大2×2=4倍,体积扩大2×2×2=8倍.
故答案为:4,8.
【点评】考查了正方体的体积,正方体的表面积和正方体棱长的关系,是基础题型,比较简单.
5.【分析】根据倍数关系的最大公因数是较小数,最小公倍数是较大数,24和48是倍数关系,据此解答.
【解答】解;24和48是倍数关系,
所以24和48的最大公因数是24,
最小公倍数是48;
故答案为:24,48.
【点评】本题主要考查求两个数的最大公因数和最小公倍数的方法,注意倍数关系的最大公因数是较小数,最小公倍数是较大数.
6.【分析】低级单位立方厘米化高级单位立方分米除以进率1000;
高级单位立方米化低级单位立方分米乘进率1000;
立方分米与升是等量关系二者互化数值不变;
高级单位升化低级单位毫升乘进率1000。
【解答】解:
7000立方厘米=7立方分米 2立方米=2000立方分米
4000立方分米=4000升 3升=3000毫升
故答案为:7,2000,4000,3000。
【点评】立方米、立方分米(升)、立方厘米(毫升)相邻单位之间的进率是1000,由高级单位化低级单位乘进率,反之除以进率。
7.【分析】每两个队之间赛一场,那么每个队要赛3场,一共是4×3=12(场),但是两队比赛是同一场比赛,所以12场比赛就多算了一倍,再除以2即可。
【解答】解:4×(4﹣1)÷2
=4×3÷2
=6(场)
答:一共要进行6场比赛。
故答案为:6。
【点评】本题属于握手问题,可利用握手问题的公式求解:握手次数=人数×(人数﹣1)÷2进行求解。
8.【分析】根据长方体棱长总和公式:棱长=(长+宽+高)×4,表面积公式:表面积=(长×宽+长×高+宽×高)×2,体积公式:体积=长×宽×高,代入数字即可求解。
【解答】解:棱长总和:(6+5+5)×4
=16×4
=64(分米)
表面积:(6×5+6×5+5×5)×2
=(30+30+25)×2
=85×2
=170(平方分米)
体积:6×5×5
=30×5
=150(立方分米)
答:它的棱长总和是64dm,表面积是170平方分米,体积是150立方分米。
故答案为:64;170平方分米;150立方分米。
【点评】此题主要考查长方体的棱长总和公式,表面积公式、体积公式的运用,关键是要熟记公式。
二、判断。(对的打“√”,错的打“×”。)(6分)
9.【分析】根据轴对称图形的含义:如果一个图形沿一条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;因为平行四边形不是轴对称图形,所以没有对称轴,进而判断即可.
【解答】解:根据轴对称图形的含义可知:平行四边形不是轴对称图形,所以没有对称轴.
故答案为:×.
【点评】判断轴对称的关键是寻找对称轴,两边图形对折后可完全重合.
10.【分析】分别把5米和6米看作单位“1”,根据一个数乘分数的意义,用乘法分别求出5米的是多少米、6米的是多少米,然后进行比较即可.
【解答】解:5×(米)
6×(米)
米
所以原题说法错误;
故答案为:×.
【点评】此题考查的目的是理解掌握一个数乘分数的意义及应用,以及分数大小比较的方法.
11.【分析】正方体的表面积和体积单位不相同,没法比较它们的大小,由此就解决即可.
【解答】解:因为正方体的表面积和体积单位不相同,没法比较它们的大小,
所以原题说法是错误的.
故答案为:×.
【点评】比较两个数的大小必须是统一单位下,面积和体积的单位不同,没法比较.
12.【分析】倒数的意义:乘积是1的两个数互为倒数。
【解答】解:根据倒数的定义可知:0和任何数相乘都得0,所以0没有倒数,其它的自然数都有倒数,原题说法正确。
故答案为:√。
【点评】要熟练掌握求倒数的方法:求一个分数的倒数,把这个分数分子和分母互换位置,求小数的倒数时,要先把小数化成分数。
13.【分析】把第一根的原来的长度看成单位“1”,那么剩下的长度就是原来的(1﹣),用原来的长度乘上这个分率就是剩下的长度;
用第二个原来的长度减去米就是第二根剩下的长度;比较两根剩下的长度即可判断.
【解答】解:1﹣=(米)
1×(1﹣)
=1×
=(米)
两根剩下的长度都是米,所以剩下的长度一样.
故答案为:√.
【点评】此题重在区分分数在具体的题目中的区别:在具体的题目中,带单位是一个具体的数,不带单位是把某一个数量看单位“1”,是它的几分之几.
14.【分析】因为真分数小于1,一个不为零的数除以一个真分数,即除以一个小于1的数,商一定会比原数小。由此解答即可。
【解答】解:因为真分数小于1,一个不为零的数除以一个真分数,即除以一个小于1的数,所以商一定会比原数小。
故答案为:√。
【点评】此题考查商的变化规律。
三、选择。(将正确答案的序号填在括号里。)(6分)
15.【分析】圆有无数条对称轴,每条直径所在的直线,都是它的对称轴;
分母是9的真分数的分子可以是1、2、3、4、5、6、7、8共8个;
把这根绳子的长度看作单位“1”,对折两次后,长度是这根绳子长度的,根据分数除法的意义,即可求出这根绳子的长度;
根据升与立方分米的关系,1升=1立方分米。
【解答】解:圆有无数条对称轴。A说法正确;
分母是9的真分数有:、、、、、、、共8个。B说法正确;
÷=2(米)
一根绳子对折两次后是米,这根绳子长2米。C说法错误;
1升=1立方分米。D说法正确。
故选:C。
【点评】此题考查的知识点:圆的特征及轴对称图形的意义;真分数的意义;分数除法的意义及应用;体积(容积)单位间的进率。
16.【分析】根据为倍数关系的两个数的最大公因数是较小的数,最小公倍数是较大的数,分别求出四个选项中两个数的最大公因数和最小公倍数即可选择。
【解答】解:A.36是6的倍数,所以6和36的最大公因数是6,最小公倍数是36;
B.36是12的倍数,所以12和36的最大公因数是12,最小公倍数是36;
C.18是6的倍数,所以6和18的最大公因数是6,最小公倍数是18;
D.12是6的倍数,所以6和12的最大因数是6,最小公倍数是12。
所以这两个数可能是6和36。
故选:A。
【点评】熟练掌握为倍数关系的两个数的最大公因数是较小的数,最小公倍数是较大的数是解题的关键。
17.【分析】设A×=B×=C×=a(a≠0),再用a分别表示出A、B、C,即可比较出A、B、C的大小。
【解答】解:设A×=B×=C×=a(a≠0),
则A×=a,A=;
B×=a,B=2a;
C×=a,C=a;
2a>>a,
所以B>A>C,最大的是B。
故选:B。
【点评】本题可通过用一个中间数a表示出A、B、C的方法来比较A、B、的大小。
18.【分析】根据长方体的棱长总和=(长+宽+高)×4,求出这根铁丝的长度,然后用这根铁丝的长度除以12即可求出正方体的棱长。
【解答】解:(16+14+6)×4÷12
=36×4÷12
=144÷12
=12(厘米)
答:正方体的棱长是12厘米。
故选:C。
【点评】此题主要考查长方体、正方体棱长总和公式的灵活运用,关键是熟记公式。
19.【分析】根据正方体展开图的11种特征,图A不属于正方体展开图;图B属于正方体展开图的“2﹣2﹣2”结构;图C属于正方体展开图的“1﹣3﹣2”结构;图D属于正方体展开图的“1﹣4﹣1”结构。
【解答】解:不是正方体的展开图。
故选:A。
【点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
20.【分析】因为两个小组都参加的学生是参加音乐小组和美术小组的学生的重叠部分,所以根据容斥原理列式为:25+23﹣40=8(名);据此解答。
【解答】解:25+23﹣40
=48﹣40
=8(名)
答:两个小组都参加的学生有8名。
故选:A。
【点评】本题考查了容斥原理,关键是理解40人包括三部分的人数,知识点是:总人数=(A+B)﹣既A又B。
四、计算。(29分)
21.【分析】根据分数加减乘除法的计算方法求解即可。
【解答】解:
+= += ﹣= ÷10=
2×= ÷=5 += ×=
【点评】本题考查了简单的分数计算,计算时要细心,注意把结果化成最简分数。
22.【分析】(1)根据加法交换律进行计算;
(2)先算小括号里面的减法,再算括号外面的乘法;
(3)根据乘法分配律进行计算;
(4)先算除法,再算加法。
【解答】解:(1)++
=++
=1+
=1
(2)(3﹣)×
=×
=
(3)×+×
=×(+)
=×1
=
(4)+÷
=+
=
【点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
23.【分析】(1)根据等式的性质,方程两边同时减去求解;
(2)根据等式的性质,方程两边同时除以求解;
(3)根据等式的性质,方程两边同时加上x,再两边同时减去求解。
【解答】解:(1)+x=
+x﹣=﹣
x=
(2)x=
x÷=÷
x=
(3)1﹣x=
1﹣x+x=+x
1=+x
1﹣=+x﹣
x=
【点评】此题考查了学生根据等式的性质解方程的能力,注意等号对齐。
五、动手操作。(18分)
24.【分析】(1)(2)根据旋转的意义,找出图中长方形、小旗的关键处,再画出按逆时针方向旋转90度后的形状即可。
(3)根据平移图形的特征,把平行四边形C的四个顶点分别向左平移3格,再向下平移1格,再首尾连接各点,即可得到平行四边形C左移动3格,再向下移动1格后的图形。
【解答】解:如图;
。
【点评】本题考查了图形的旋转变化、平移变化,学生主要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错。
25.【分析】(1)根据统计表中A品牌的数据在统计图中描点,用实线连线,根据统计表中B品牌的数据在统计图中描点,用虚线连线;
(2)分别计算出两种品牌电视的全年总销售,再进行大小比较;
(3)6月份两种电视在统计图中垂直位置最近,所以6月份两种电视销量最接近;1月份两种电视在统计图中垂直位置最远,所以1月份两种电视销量相差最大;
(4)从图中可以看出A品牌的销量呈下降趋势;B品牌的销量呈上升趋势,所以进电视时,要多进些B品牌。(答案不唯一)
【解答】解:(1)折线统计图如下:
(2)75+80+62+45+55+48+40+42+35+32+36+30=580(台)
30+40+42+45+50+50+52+40+42+50+43+52=536(台)
580>536
答:A品牌电视全年总销最高。
(3)6月份两种电视销量最接近,1月份两种电视销量相差最大。
(4)从图中可以看出A品牌的销量呈下降趋势;B品牌的销量呈上升趋势,所以进电视时,要多进些B品牌。(答案不唯一)
【点评】本题考查根据统计表中数据填补复式折线统计图,然后再根据统计图中的信息解决问题。
六、解决问题。(21分)
26.【分析】根据底面周长乘以通风管的长度就是通风管的表面积,代入数字即可求解。
【解答】解:1×4×10
=4×10
=40(平方分米)
答:做这个通风管至少需要40平方分米的铁皮。
【点评】通风管只要侧面积,本题运用“底面周长×长度=侧面积”进行计算即可。
27.【分析】根据题意,把整条路的长度看作单位“1”,则用总长度减去前两周修的长度,计算第三周修的长度即可。
【解答】解:400﹣400×﹣400×
=400﹣80﹣150
=170(米)
答:第三周修170米。
【点评】本题主要考查分数四则运算的应用,关键找对单位“1”,利用数量关系做题。
28.【分析】根据题意可知,把铁块从水缸中取出后,下降部分水的体积就等于这个铁块的体积,再根据长方体的体积公式:V=Sh,那么h=V÷S,用铁块的体积除以铁块的底面积就是铁块的长。
【解答】解:3.5×2.4×0.3÷2.1
=8.4×0.3÷2.1
=2.52÷2.1
=1.2(米)
答:那么它的长是1.2米。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
29.【分析】把甲乙两地之间的路程看作单位“1”,已经行驶全长的,那么剩下的路程占全程的(1),根据已知一个数的几分之几是多少,求这个数,用除法解答。
【解答】解:280÷(1)
=
=
=490(千米)
答:甲乙两地相距490千米。
【点评】此题属于基本的分数除法应用题,关键是确定单位“1”,利用基本数量关系解决问题。
30.【分析】因为只有四周墙壁贴瓷砖,所以首先根据长方体的表面积公式:(长×高+宽×高)×2,求出4面墙壁的面积,再根据正方形的面积公式:S=a2,求出每块瓷砖的面积,然后用墙壁的面积除以每块瓷砖的面积求出需要的块数,再根据单价×数量=总价,据此列式解答。
【解答】解:40厘米=0.4米
(3.2×2.4+2×2.4)×2÷(0.4×0.4)×8
=(7.68+4.8)×2÷0.16×8
=12.48×2÷0.16×8
=24.96÷0.16×8
=156×8
=1248(元)
答:一共需要1248元。
【点评】此题主要考查长方体表面积公式在实际生活中的应用,关键是熟记公式。
31.【分析】高增加2厘米,表面积就增加了一个高为2厘米的长方体的侧面积,用40除以这个长方形的高,可得底面周长,再除以4就是原长方体长和宽的长,再根据长方体的体积公式可求出原来长方体的体积;据此解答。
【解答】解:40÷2÷4=5(厘米)
(5﹣2)×5×5
=3×5×5
=75(立方厘米)
答:原来长方体的体积是75立方厘米。
【点评】本题的关键是让学生理解:高增加2厘米,表面积就增加了一个高为2厘米的长方体的侧面积。
同课章节目录
