8.2消元——解二元一次方程组(2)
文档属性
| 名称 | 8.2消元——解二元一次方程组(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 689.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-14 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
(第2课时)
8.2 消元—解二元一次方程组
上一课时学习了用代入消元法解二元一次方程组,本课时既要巩固对解法的掌握,又要达到对解法的熟练运用.
课件说明
学习目标:
(1)会用代入消元法解二元一次方程组.
(2)初步感受运用二元一次方程组解决实际问题的过程.
学习重点:
根据实际问题列出二元一次方程组,并用代入消元法求解.
课件说明
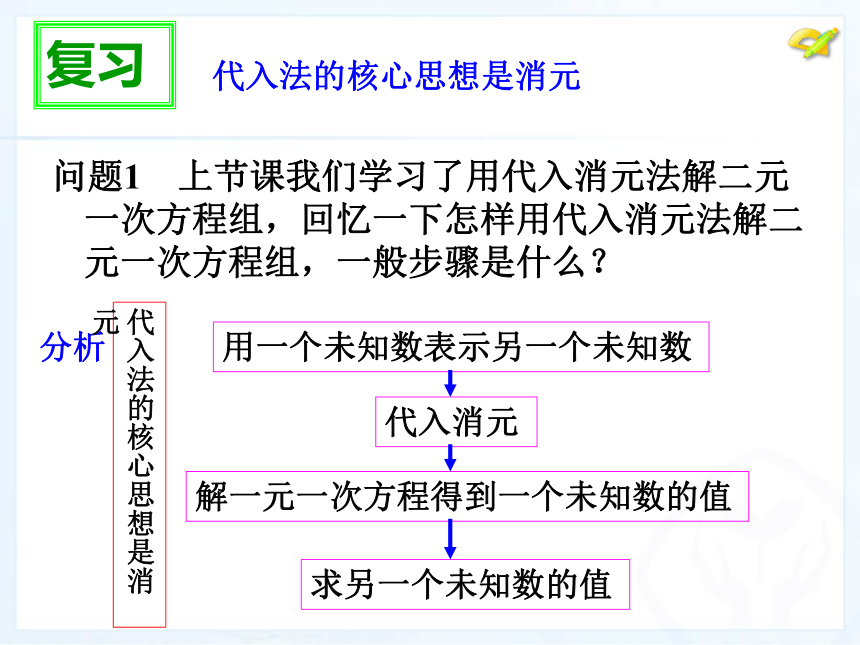
问题1 上节课我们学习了用代入消元法解二元一次方程组,回忆一下怎样用代入消元法解二元一次方程组,一般步骤是什么?
复习
代入法的核心思想是消元
分析
用一个未知数表示另一个未知数
代入消元
解一元一次方程得到一个未知数的值
求另一个未知数的值
代入法的核心思想是消元
问题2
你能用代入消元法解方程组 吗?
复习
复习
解:由①,得
③
把③代入②,得
①
②
代入③得
所以, 是这个二元一次方程组的解.
例2的教学
问题3 例2中有哪些未知量?
答:未知量有消毒液应该分装的大瓶数和小瓶数.所以可设这些消毒液应分装大瓶和小瓶的数量分别为x、y.
教科书例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装( 250 g )两种产品的销售数量(按瓶计算)比为2︰5.某厂每天生产这种消毒液22.5 t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
例2的教学
问题4 例2中有哪些等量关系?
答:等量关系包括:大瓶数︰小瓶数=2︰5;
大瓶所装消毒液+小瓶所装消毒液=22.5(t)
教科书例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装( 250 g )两种产品的销售数量(按瓶计算)比为2︰5.某厂每天生产这种消毒液22.5 t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
例2的教学
等量关系:
大瓶数︰小瓶数=2︰5;
大瓶所装消毒液+小瓶所装消毒液=22.5 t
问题5 如何用二元一次方程组表示上面的两个等量关系?
正确列法:
例2的教学
问题列法1:
(1)估算一下方程②的解是自然数吗?
(2)符合实际意义吗?
(3)仔细审题,造成上述问题的原因是什么?
分析:
①
②
例2的教学
问题列法1:
(1)估算一下方程②的解是自然数吗?
(2)符合实际意义吗?
(3)仔细审题,造成上述问题的原因是什么?
分析:
①
②
例2的教学
问题列法2:
(1)这个方程组是二元一次方程组吗?为什么?
(2)如何得到二元一次方程组?
分析:
问题6 请你用代入消元法解上面的方程组.
例2的教学
解得
答:这些消毒液应该分装20 000大瓶和50 000小瓶.
问题7 阅读教材上的框图,你能结合框图简述例2的解题过程吗?
例2的教学
归纳总结
问题8 结合例2,请你思考列方程组解决实际问题时应注意什么?
布置作业
教科书 第93页 练习第4题
(第2课时)
8.2 消元—解二元一次方程组
上一课时学习了用代入消元法解二元一次方程组,本课时既要巩固对解法的掌握,又要达到对解法的熟练运用.
课件说明
学习目标:
(1)会用代入消元法解二元一次方程组.
(2)初步感受运用二元一次方程组解决实际问题的过程.
学习重点:
根据实际问题列出二元一次方程组,并用代入消元法求解.
课件说明
问题1 上节课我们学习了用代入消元法解二元一次方程组,回忆一下怎样用代入消元法解二元一次方程组,一般步骤是什么?
复习
代入法的核心思想是消元
分析
用一个未知数表示另一个未知数
代入消元
解一元一次方程得到一个未知数的值
求另一个未知数的值
代入法的核心思想是消元
问题2
你能用代入消元法解方程组 吗?
复习
复习
解:由①,得
③
把③代入②,得
①
②
代入③得
所以, 是这个二元一次方程组的解.
例2的教学
问题3 例2中有哪些未知量?
答:未知量有消毒液应该分装的大瓶数和小瓶数.所以可设这些消毒液应分装大瓶和小瓶的数量分别为x、y.
教科书例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装( 250 g )两种产品的销售数量(按瓶计算)比为2︰5.某厂每天生产这种消毒液22.5 t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
例2的教学
问题4 例2中有哪些等量关系?
答:等量关系包括:大瓶数︰小瓶数=2︰5;
大瓶所装消毒液+小瓶所装消毒液=22.5(t)
教科书例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装( 250 g )两种产品的销售数量(按瓶计算)比为2︰5.某厂每天生产这种消毒液22.5 t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
例2的教学
等量关系:
大瓶数︰小瓶数=2︰5;
大瓶所装消毒液+小瓶所装消毒液=22.5 t
问题5 如何用二元一次方程组表示上面的两个等量关系?
正确列法:
例2的教学
问题列法1:
(1)估算一下方程②的解是自然数吗?
(2)符合实际意义吗?
(3)仔细审题,造成上述问题的原因是什么?
分析:
①
②
例2的教学
问题列法1:
(1)估算一下方程②的解是自然数吗?
(2)符合实际意义吗?
(3)仔细审题,造成上述问题的原因是什么?
分析:
①
②
例2的教学
问题列法2:
(1)这个方程组是二元一次方程组吗?为什么?
(2)如何得到二元一次方程组?
分析:
问题6 请你用代入消元法解上面的方程组.
例2的教学
解得
答:这些消毒液应该分装20 000大瓶和50 000小瓶.
问题7 阅读教材上的框图,你能结合框图简述例2的解题过程吗?
例2的教学
归纳总结
问题8 结合例2,请你思考列方程组解决实际问题时应注意什么?
布置作业
教科书 第93页 练习第4题
