冀教版数学七年级下册 7.2 相交线课件(共17张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 7.2 相交线课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 382.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 11:47:44 | ||
图片预览




文档简介
(共17张PPT)
相交线
节日的夜晚,广场上两个激光发射器发射出在同一平面上的两束光线,如果将这两束光线看成两条直线,那么当发射器左右摆动时,这两条直线有什么样的位置关系
观 察 与 思 考
A
O
2
4
1
3
B
C
D
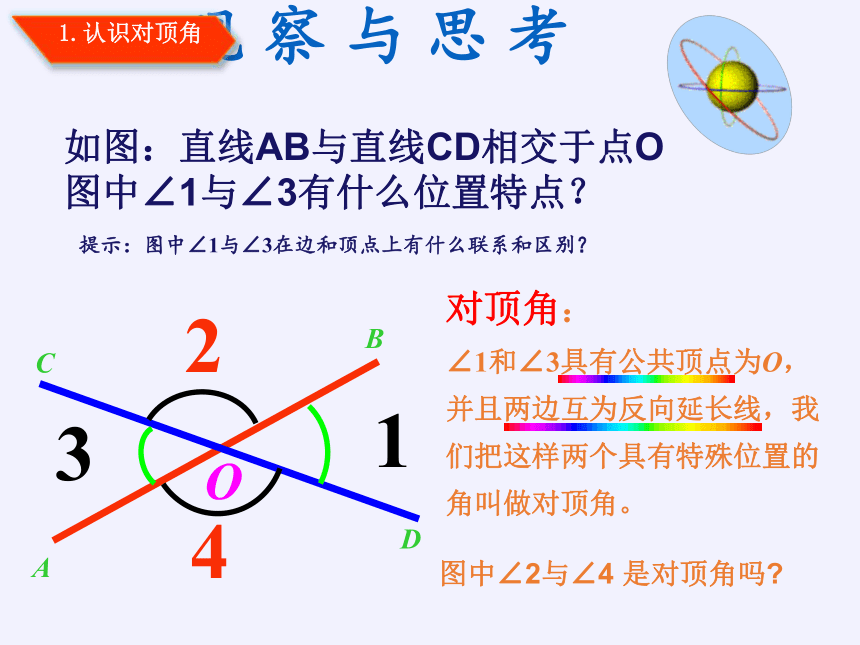
如图:直线AB与直线CD相交于点O
图中∠1与∠3有什么位置特点?
对顶角:
∠1和∠3具有公共顶点为O,
并且两边互为反向延长线,我
们把这样两个具有特殊位置的
角叫做对顶角。
图中∠2与∠4 是对顶角吗
1.认识对顶角
提示:图中∠1与∠3在边和顶点上有什么联系和区别?
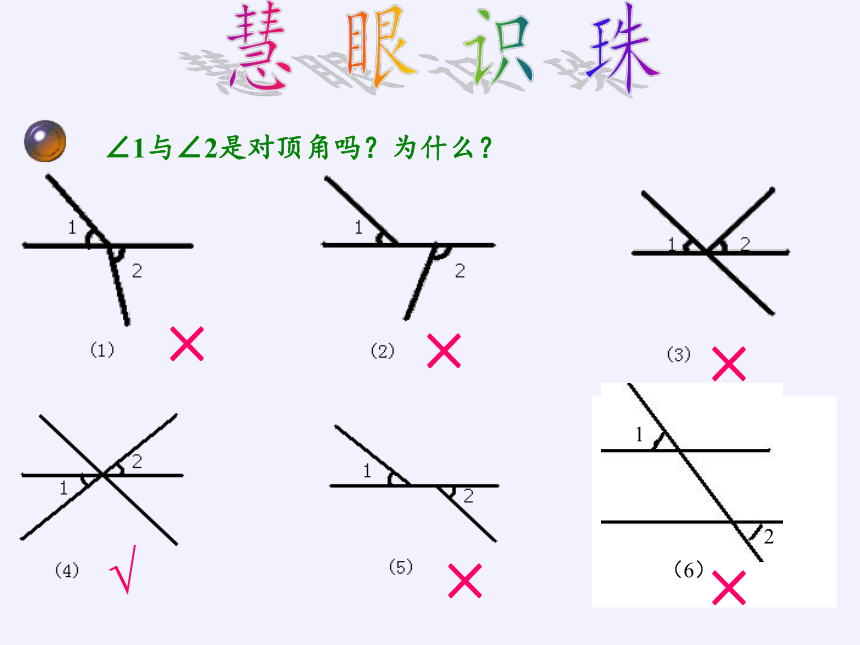
慧 眼 识 珠
∠1与∠2是对顶角吗?为什么?
×
√
×
×
×
×
1
2
(6)
×
(一)活动目的:
探索对顶角的性质.
(二)活动步骤:
1、操作:拿出预先准备好的两根木条,将一根木条固定,转动另一根木条,这时∠1和∠3同时 或同时 。
2、猜想: ∠1和∠3的大小关系。
3、讨论:请用适当的方法验证你的猜想。
你有几种方法?
O
1
2
3
4
实 验 探 究
2.探索对顶角的性质
增大
减小
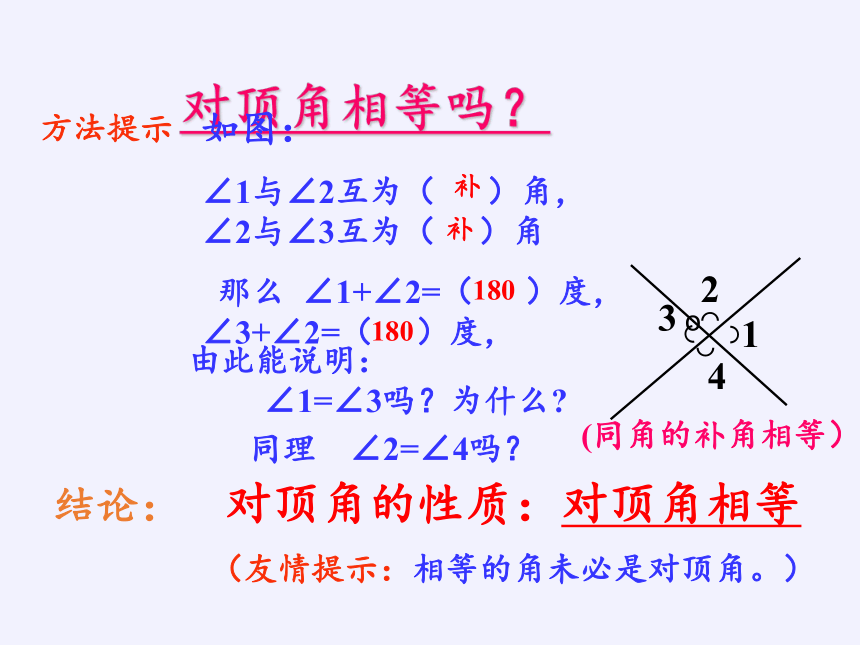
对顶角相等吗?
如图:
∠1与∠2互为( )角, ∠2与∠3互为( )角
那么 ∠1+∠2=( )度, ∠3+∠2=( )度,
方法提示
结论: 对顶角的性质:对顶角相等
2
⌒
⌒
⌒
4
3 o
1
⌒
补
补
180
180
由此能说明:
∠1=∠3吗?为什么
同理 ∠2=∠4吗?
(同角的补角相等)
(友情提示:相等的角未必是对顶角。)
观察∠4和∠8,分别在直线a,b
的 ,在直线c的 ;∠3和∠7分别在直线a,b
的 ,直线c的 。
5
1
6
8
7
2
4
3
a
c
b
把具有这样位置的一对角,叫做同位角。
同侧
同旁
同旁
同侧
3.同位角
同位角在图中表现为不规则“ ”型.
F
“三线八角”图形。
直线a、b被直线c所截,形成
观察∠3和∠6,分别在直线a,b的 ,在直线c的 ;把具有∠3和∠6这样位置关系的一对角,叫做 。
内部
两旁
类比学习 事半功倍
5
1
6
8
7
2
4
3
a
c
b
内错角在图形中表现为不规则“ ”型
Z
内错角
我们把具有∠3与∠5这样位置的一对角,叫做同旁内角。
同旁内角是指位于直线c的同旁,直线a和b内部的两个角。
合作探究:
你能说出具有什么关系的一对角叫做同旁内角吗?
5
1
6
8
7
2
4
3
a
c
b
同旁内角在图形中表现为不规则“ ”型
u、n、c
请同学们伸出双手,分别用双手的大拇指和食指各组成一个角,两食指成一条线,保持在同一平面内,分别进行尝试,看一看,你能组成同位角、内错角、同旁内角吗?
互动游戏
4.试一试
角的名称 基 本 图 形 位 置 特 征 与被截线的位置关系 与截线的位置关系 基本
字母形状
同 侧 同 旁
内 部 两 旁
内 部 同 旁
同 位 角
内 错 角
同 旁
内 角
F
Z
U
大家谈谈
5.大家谈谈
名称 对数 举例
对顶角
同位角
内错角
同旁内角
1、直线AB 、CD被直线EF所截,交点分别为G ,H,所有的同位角、内错角、同旁内角、对顶角各有多少对?
A
E
G
B
H
C
D
做做 练练
3
1
2
4
5
7
8
6
4
4
2
2
巩固练习强化新知
F
∠2与∠3
∠2与∠6
∠3与∠6
∠3与∠5
2、找出图中的同位角、内错角 、同旁内角:
F
A
B
C
D
E
火眼金睛
巩固练习强化新知
3、星期天,小刚和爸爸一起去河边钓鱼,河对岸有两棵树(A、B),河边有一棵树(C):结合平时的学习,小明想出来一个问题“如何测量∠ ACB的大小?”
生活中的问题
巩固练习 强化新知
学以 致用
D
E
课堂小结 交流评价
我的收获是…
(可以是知识方面,也可以是思想或情感方面,如对自己的表现感想如何…对同伴的感想如何…我从同学身上学到了…)
通过本节课的探索与交流
二、第36页习题1,2,3
布置 作业
一 、寻找生活中对顶角、同位角、
内错角、同旁内角的实例。
谢 谢
相交线
节日的夜晚,广场上两个激光发射器发射出在同一平面上的两束光线,如果将这两束光线看成两条直线,那么当发射器左右摆动时,这两条直线有什么样的位置关系
观 察 与 思 考
A
O
2
4
1
3
B
C
D
如图:直线AB与直线CD相交于点O
图中∠1与∠3有什么位置特点?
对顶角:
∠1和∠3具有公共顶点为O,
并且两边互为反向延长线,我
们把这样两个具有特殊位置的
角叫做对顶角。
图中∠2与∠4 是对顶角吗
1.认识对顶角
提示:图中∠1与∠3在边和顶点上有什么联系和区别?
慧 眼 识 珠
∠1与∠2是对顶角吗?为什么?
×
√
×
×
×
×
1
2
(6)
×
(一)活动目的:
探索对顶角的性质.
(二)活动步骤:
1、操作:拿出预先准备好的两根木条,将一根木条固定,转动另一根木条,这时∠1和∠3同时 或同时 。
2、猜想: ∠1和∠3的大小关系。
3、讨论:请用适当的方法验证你的猜想。
你有几种方法?
O
1
2
3
4
实 验 探 究
2.探索对顶角的性质
增大
减小
对顶角相等吗?
如图:
∠1与∠2互为( )角, ∠2与∠3互为( )角
那么 ∠1+∠2=( )度, ∠3+∠2=( )度,
方法提示
结论: 对顶角的性质:对顶角相等
2
⌒
⌒
⌒
4
3 o
1
⌒
补
补
180
180
由此能说明:
∠1=∠3吗?为什么
同理 ∠2=∠4吗?
(同角的补角相等)
(友情提示:相等的角未必是对顶角。)
观察∠4和∠8,分别在直线a,b
的 ,在直线c的 ;∠3和∠7分别在直线a,b
的 ,直线c的 。
5
1
6
8
7
2
4
3
a
c
b
把具有这样位置的一对角,叫做同位角。
同侧
同旁
同旁
同侧
3.同位角
同位角在图中表现为不规则“ ”型.
F
“三线八角”图形。
直线a、b被直线c所截,形成
观察∠3和∠6,分别在直线a,b的 ,在直线c的 ;把具有∠3和∠6这样位置关系的一对角,叫做 。
内部
两旁
类比学习 事半功倍
5
1
6
8
7
2
4
3
a
c
b
内错角在图形中表现为不规则“ ”型
Z
内错角
我们把具有∠3与∠5这样位置的一对角,叫做同旁内角。
同旁内角是指位于直线c的同旁,直线a和b内部的两个角。
合作探究:
你能说出具有什么关系的一对角叫做同旁内角吗?
5
1
6
8
7
2
4
3
a
c
b
同旁内角在图形中表现为不规则“ ”型
u、n、c
请同学们伸出双手,分别用双手的大拇指和食指各组成一个角,两食指成一条线,保持在同一平面内,分别进行尝试,看一看,你能组成同位角、内错角、同旁内角吗?
互动游戏
4.试一试
角的名称 基 本 图 形 位 置 特 征 与被截线的位置关系 与截线的位置关系 基本
字母形状
同 侧 同 旁
内 部 两 旁
内 部 同 旁
同 位 角
内 错 角
同 旁
内 角
F
Z
U
大家谈谈
5.大家谈谈
名称 对数 举例
对顶角
同位角
内错角
同旁内角
1、直线AB 、CD被直线EF所截,交点分别为G ,H,所有的同位角、内错角、同旁内角、对顶角各有多少对?
A
E
G
B
H
C
D
做做 练练
3
1
2
4
5
7
8
6
4
4
2
2
巩固练习强化新知
F
∠2与∠3
∠2与∠6
∠3与∠6
∠3与∠5
2、找出图中的同位角、内错角 、同旁内角:
F
A
B
C
D
E
火眼金睛
巩固练习强化新知
3、星期天,小刚和爸爸一起去河边钓鱼,河对岸有两棵树(A、B),河边有一棵树(C):结合平时的学习,小明想出来一个问题“如何测量∠ ACB的大小?”
生活中的问题
巩固练习 强化新知
学以 致用
D
E
课堂小结 交流评价
我的收获是…
(可以是知识方面,也可以是思想或情感方面,如对自己的表现感想如何…对同伴的感想如何…我从同学身上学到了…)
通过本节课的探索与交流
二、第36页习题1,2,3
布置 作业
一 、寻找生活中对顶角、同位角、
内错角、同旁内角的实例。
谢 谢
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
