冀教版数学七年级下册 8.2 单项式乘以单项式课件(共25张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 8.2 单项式乘以单项式课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
使 用 目 的
设 计 思 路
用 后 反 思
学习过程
制作和使用本课件的目的是给学生以知识的启迪、艺术的享受,使课堂气氛活跃,学生学习轻松愉快,即能提高课堂效率、加大教学容量,又有利于发挥学生的积极性、主动性和创造性。
使用目的
1、本节课要使学生进一步感受数形结合的魅力,从几何与代数两个角度探索单项式与单项式相乘的法则。从而培养学生探求事物发展的内在规律的良好习惯。
2、培养学生的观察、归纳、计算能力,培养学生的合作交流意识和探索精神.
设计思路
使用该多媒体课件辅助教学,优化了课堂教学结构,激发了学生的学习兴趣,使学生在参与和体验的过程中养成勇于探索、敢于实践的个性品质。充分发挥了学生的主观能动性,体现了学生是学习的主体,真正成为学习的主人,转变了角色。
用后反思
重点:单项式乘法法则及其应用。
难点:理解运算法则及其探索过程
温故知新:
判断并纠错:并说出其中所使用的性质名称与法则
①m2 ·m3=m6 ( )
②(a5)2=a7( )
③(ab2)3=ab6( )
④m5+m5=m10( )
⑤ (-x)3·(-x)2=-x5 ( )
×
m5
×
a10
×
a3b6
×
2m5
√
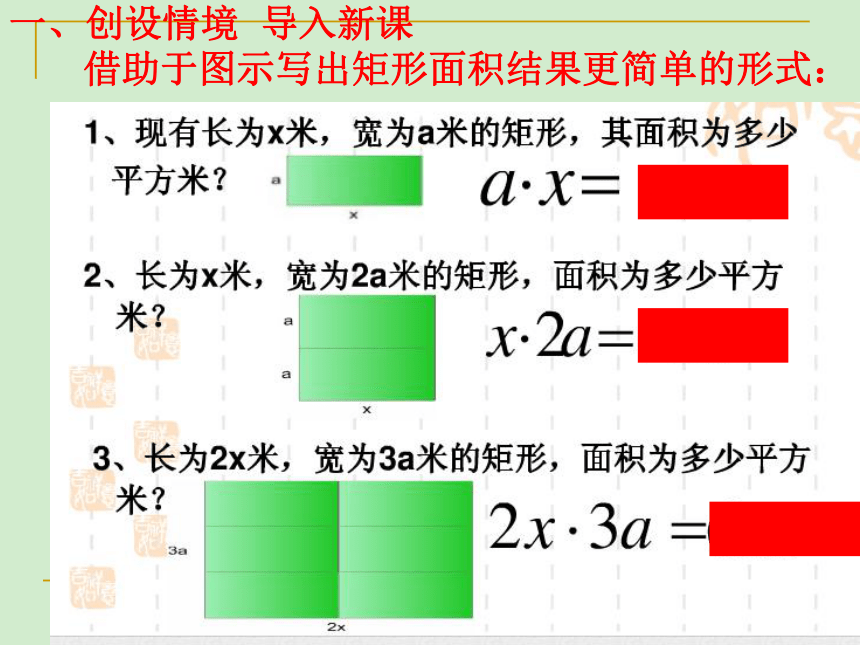
一、创设情境 导入新课
借助于图示写出矩形面积结果更简单的形式:
2、
1、 ac5·bc2
ac5 bc2是两个单项式ac5与bc2相乘,我们可以利用乘法交换律,结合律及同底数幂的运算性质来计算:
ac5 bc2=(a b) (c5 c2)
=abc5+2=abc7.
你能把下列结果表达的更简单一些吗?
解:原式
各因数系数结合成一组
相同的字母结合成一组
系数的积作为积的系数
对于相同的字母,用它们的指数和作为积里这个字母的指数
对于只有一个单项式里含有的字母,连同它的指数作为积的一个因式
例1
单项式乘以单项式的结果仍是单项式.
注意符号
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它们的指数作为 积的一个因式。
你能总结出单项式与单项式相乘法则吗?(学习小组相互讨论总结一下) :
3、 (2x)3(-5xy2).
观察一下,多了什么运算?
遇到积的乘方,运算时应先算什么
注意:
(1)先做乘方,再做单项式相乘。
(2)系数相乘不要漏掉负号
运用新知,体验成功(组内PK):
1、 (-2a2b)(-3a);
2、 (-5a2b3 )·(-4b2c);
解2 、 (-5a2b3 )·(-4b2c)
=[(-5) ×(-4)] · a2 ·(b3 ·b2) ·c
=20 a2 b5 c
解题格式规范训练
解1、 (-2a2b)(-3a)
= [(-2)×(-3)](a2 a)b
= 6a3b
3、 (2x)3(-5xy2).
解: (2x)3(-5xy2)
=8x3(-5xy2)
=[8×(-5)](x3 x)y2
=-40x4y2
一、精心选一选:
1、下列计算中,正确的是( )
A、2a3·3a2=6a6 B、4x3·2x5=8x8
C、2X·2X5=4X5 D、5X3·4X4=9X7
2、下列运算正确的是( )
A、X2·X3=X6 B、X2+X2=2X4
C、(-2X)2=-4X2 D、(-2X2)(-3X3)=6x5
B
D
3、下列等式①a5+3a5=4a5 ②2m2· m4=m8
③2a3b4(-ab2c)2=-2a5b8c2 ④(-7x) · x2y=-4x3y中,正确的有( )个。
A、1 B、2 C、3 D、4
4、如果单项式-3x4a-by2与 x3ya+b是同类项,那么这两个单项式的积是( )
A、x6y4 B、-x3y2 C 、x3y2 D、 -x6y4
B
D
×
×
×
×
(1)4a2 2a4 = 8a8 ( )
(2)6a3 5a2=11a5 ( )
(3)(-7a) (-3a3) =-21a4 ( )
(4)3a2b 4a3=12a5 ( )
系数相乘
同底数幂的乘法,底数不变,指数相加
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
求系数的积,应注意符号
二、判断正误(我能行)
下面的计算对不 对?如果不对,怎样改正?
⑴
⑷
⑶
⑵
⑸
?
(6)3x2·4x2 =12x2
5
6
x
(7) 5y3·3y5=15y15
4
12
x
8
15
y
求系数的积,应注意符号;
相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏;
单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;
单项式乘法的法则对于三个以上的单项式相乘同样适用。
若某一单项式是乘方的形式时,要先乘方再算乘法
总结进行单项式的乘法运算时的 注意事项:
(1) -5a3b2c·3a2b=
(2) x3y2·(-xy3)2=
(3) (-9ab2) ·(-ab2)2=
(4) (2ab)3·(-a2c)2=
-15a5b3c
x5y8
-9a3b6
8a7b3c2
-12a3b3
4a10
组内PK(总分100)
(7) 3y(-2x2y2) =
(8) 3a3b·(-ab3c2) =
-6x2y3
-3a4b4c2
若n为正整数,且x3n=2,求2x2n ·x4n+x4n ·x5n的值。
解: 2x2n ·x4n+x4n ·x5n
=2x6n+x9n
=2(x3n)2+(x3n)3
=2×22+23
=8+8
=16
∴原式的值等于16。
作业
必做题:课本80页练习A、B组题
选做题:导学案练习1,2
我知道了… …
我感受了… …
我做了… …
返回首页
使 用 目 的
设 计 思 路
用 后 反 思
学习过程
制作和使用本课件的目的是给学生以知识的启迪、艺术的享受,使课堂气氛活跃,学生学习轻松愉快,即能提高课堂效率、加大教学容量,又有利于发挥学生的积极性、主动性和创造性。
使用目的
1、本节课要使学生进一步感受数形结合的魅力,从几何与代数两个角度探索单项式与单项式相乘的法则。从而培养学生探求事物发展的内在规律的良好习惯。
2、培养学生的观察、归纳、计算能力,培养学生的合作交流意识和探索精神.
设计思路
使用该多媒体课件辅助教学,优化了课堂教学结构,激发了学生的学习兴趣,使学生在参与和体验的过程中养成勇于探索、敢于实践的个性品质。充分发挥了学生的主观能动性,体现了学生是学习的主体,真正成为学习的主人,转变了角色。
用后反思
重点:单项式乘法法则及其应用。
难点:理解运算法则及其探索过程
温故知新:
判断并纠错:并说出其中所使用的性质名称与法则
①m2 ·m3=m6 ( )
②(a5)2=a7( )
③(ab2)3=ab6( )
④m5+m5=m10( )
⑤ (-x)3·(-x)2=-x5 ( )
×
m5
×
a10
×
a3b6
×
2m5
√
一、创设情境 导入新课
借助于图示写出矩形面积结果更简单的形式:
2、
1、 ac5·bc2
ac5 bc2是两个单项式ac5与bc2相乘,我们可以利用乘法交换律,结合律及同底数幂的运算性质来计算:
ac5 bc2=(a b) (c5 c2)
=abc5+2=abc7.
你能把下列结果表达的更简单一些吗?
解:原式
各因数系数结合成一组
相同的字母结合成一组
系数的积作为积的系数
对于相同的字母,用它们的指数和作为积里这个字母的指数
对于只有一个单项式里含有的字母,连同它的指数作为积的一个因式
例1
单项式乘以单项式的结果仍是单项式.
注意符号
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它们的指数作为 积的一个因式。
你能总结出单项式与单项式相乘法则吗?(学习小组相互讨论总结一下) :
3、 (2x)3(-5xy2).
观察一下,多了什么运算?
遇到积的乘方,运算时应先算什么
注意:
(1)先做乘方,再做单项式相乘。
(2)系数相乘不要漏掉负号
运用新知,体验成功(组内PK):
1、 (-2a2b)(-3a);
2、 (-5a2b3 )·(-4b2c);
解2 、 (-5a2b3 )·(-4b2c)
=[(-5) ×(-4)] · a2 ·(b3 ·b2) ·c
=20 a2 b5 c
解题格式规范训练
解1、 (-2a2b)(-3a)
= [(-2)×(-3)](a2 a)b
= 6a3b
3、 (2x)3(-5xy2).
解: (2x)3(-5xy2)
=8x3(-5xy2)
=[8×(-5)](x3 x)y2
=-40x4y2
一、精心选一选:
1、下列计算中,正确的是( )
A、2a3·3a2=6a6 B、4x3·2x5=8x8
C、2X·2X5=4X5 D、5X3·4X4=9X7
2、下列运算正确的是( )
A、X2·X3=X6 B、X2+X2=2X4
C、(-2X)2=-4X2 D、(-2X2)(-3X3)=6x5
B
D
3、下列等式①a5+3a5=4a5 ②2m2· m4=m8
③2a3b4(-ab2c)2=-2a5b8c2 ④(-7x) · x2y=-4x3y中,正确的有( )个。
A、1 B、2 C、3 D、4
4、如果单项式-3x4a-by2与 x3ya+b是同类项,那么这两个单项式的积是( )
A、x6y4 B、-x3y2 C 、x3y2 D、 -x6y4
B
D
×
×
×
×
(1)4a2 2a4 = 8a8 ( )
(2)6a3 5a2=11a5 ( )
(3)(-7a) (-3a3) =-21a4 ( )
(4)3a2b 4a3=12a5 ( )
系数相乘
同底数幂的乘法,底数不变,指数相加
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
求系数的积,应注意符号
二、判断正误(我能行)
下面的计算对不 对?如果不对,怎样改正?
⑴
⑷
⑶
⑵
⑸
?
(6)3x2·4x2 =12x2
5
6
x
(7) 5y3·3y5=15y15
4
12
x
8
15
y
求系数的积,应注意符号;
相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏;
单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;
单项式乘法的法则对于三个以上的单项式相乘同样适用。
若某一单项式是乘方的形式时,要先乘方再算乘法
总结进行单项式的乘法运算时的 注意事项:
(1) -5a3b2c·3a2b=
(2) x3y2·(-xy3)2=
(3) (-9ab2) ·(-ab2)2=
(4) (2ab)3·(-a2c)2=
-15a5b3c
x5y8
-9a3b6
8a7b3c2
-12a3b3
4a10
组内PK(总分100)
(7) 3y(-2x2y2) =
(8) 3a3b·(-ab3c2) =
-6x2y3
-3a4b4c2
若n为正整数,且x3n=2,求2x2n ·x4n+x4n ·x5n的值。
解: 2x2n ·x4n+x4n ·x5n
=2x6n+x9n
=2(x3n)2+(x3n)3
=2×22+23
=8+8
=16
∴原式的值等于16。
作业
必做题:课本80页练习A、B组题
选做题:导学案练习1,2
我知道了… …
我感受了… …
我做了… …
返回首页
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
