人教版数学九年级下册第二十六章 数学活动 课件(共28张PPT)
文档属性
| 名称 | 人教版数学九年级下册第二十六章 数学活动 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 07:36:37 | ||
图片预览




文档简介
(共28张PPT)
数学活动
问题1:矩形的面积一定时,矩形的长和宽成什么关系?
问题2:如果把矩形的一个顶点固定,拖动这个固定顶点的对角顶点,拖动时必须保证矩形的面积不变,猜猜看,这个对角顶点的运动轨迹会是什么图象呢?
长
宽
面积不变
情境导入
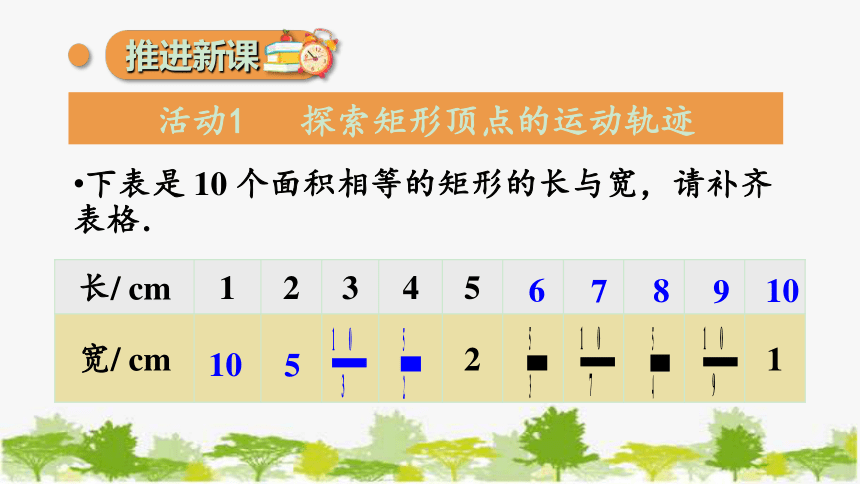
下表是 10 个面积相等的矩形的长与宽,请补齐表格.
长/ cm 1 2 3 4 5
宽/ cm 2 1
活动1 探索矩形顶点的运动轨迹
10
5
6
7
8
9
10
推进新课
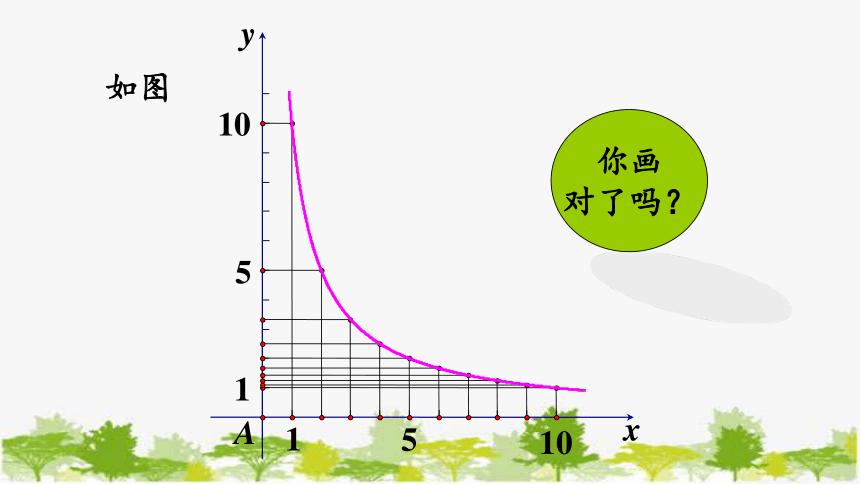
设∠A 为这 10 个矩形的公共角.画出这 10 个矩形,然后取∠A 的 10 个对角的顶点,并把这 10 个点用平滑的曲线顺次连接起来.
这条曲线是反比例函数图象的一支吗?为什么?
如图
1
A
x
y
5
10
5
10
1
你画
对了吗?
从表中数据可以看出,长方形的面积为 10,即 k = 10,矩形的长 y 是宽 x 的反比例函数,即
小结
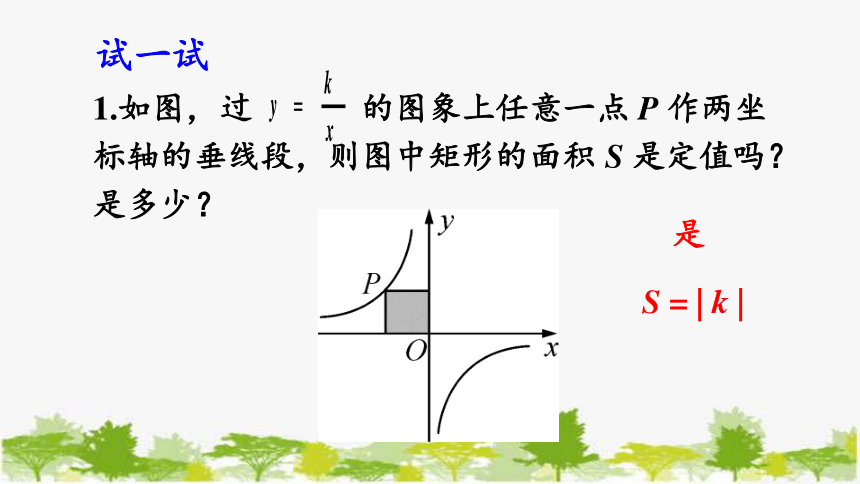
1.如图,过 的图象上任意一点 P 作两坐标轴的垂线段,则图中矩形的面积 S 是定值吗?是多少?
试一试
是
S = | k |
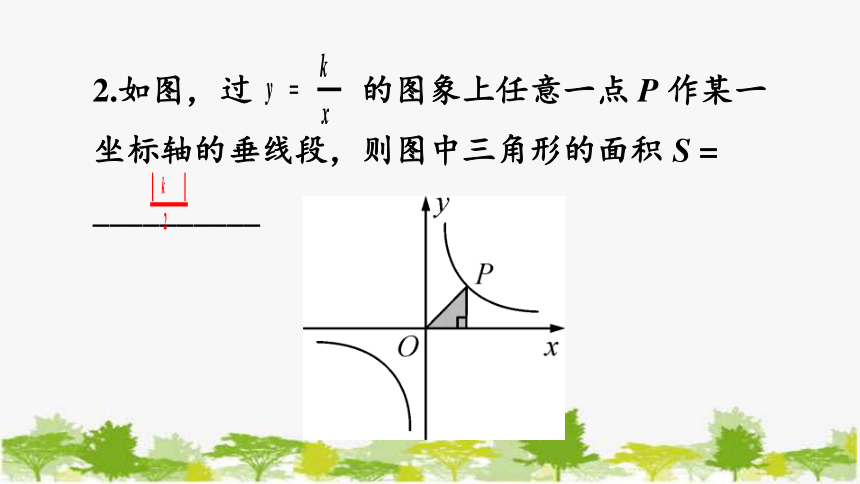
2.如图,过 的图象上任意一点 P 作某一坐标轴的垂线段,则图中三角形的面积 S = __________
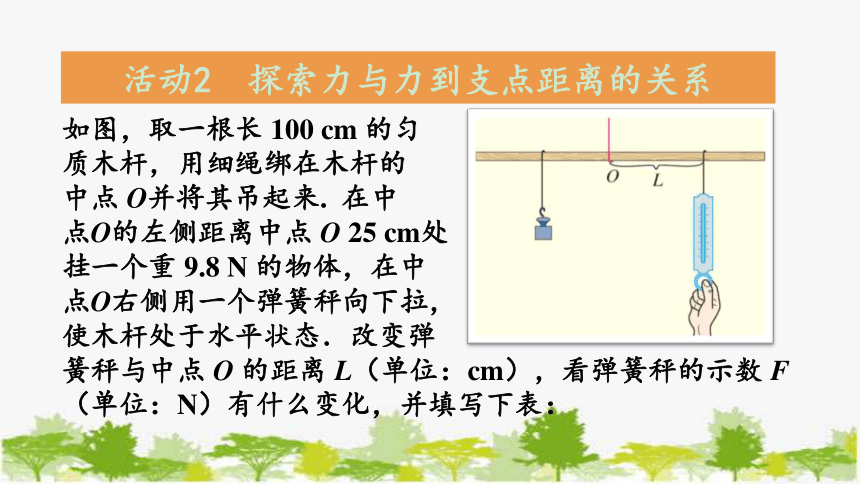
如图,取一根长 100 cm 的匀
质木杆,用细绳绑在木杆的
中点 O并将其吊起来. 在中 点O的左侧距离中点 O 25 cm处 挂一个重 9.8 N 的物体,在中 点O右侧用一个弹簧秤向下拉,
使木杆处于水平状态.改变弹
簧秤与中点 O 的距离 L(单位:cm),看弹簧秤的示数 F(单位:N)有什么变化,并填写下表:
活动2 探索力与力到支点距离的关系
以 L 的数值为横坐标,F 为纵坐标建立直角坐标系.在坐标系中描出以上表中的数对为坐标的各点,并用平滑曲线顺次连接这些点.
这条曲线是反比例函数图象的一支吗?为什么?点(50,4.9)在这条曲线上吗?
L / cm 5 10 15 20 25 30 35 40 45
F / N
杠杆的平衡条件是,作用在杠杆上的两个力的大小跟它们的力臂成反比,即
动力×动力臂 = 阻力×阻力臂
用代数式表示为
F1L1 = F2L2
式中,F1 表示动力,L1表示动力臂,F2 表示阻力,L2 表示阻力臂.从上式可以看出,欲使杠杆平衡,动力臂是阻力臂的几倍,动力就是阻力的几分之一.
杠杆的平衡条件
L / cm 5 10 15 20 25 30 35 40 45
F / N
49
24.5
16.33
12.25
9.8
8.17
7
6.125
5.44
在此活动中,弹簧秤的示数 F 是距离 L 的反比例函数,根据已知条件得
k = 9.8×25 = 245
小结
点(50,4.9)在这条曲线上.
1.如图,若点A在反比例函数 ( k ≠ 0 )的图象上,AM⊥x轴于点M,△AMO 的面积为3,则 k = _______.
– 6
基础巩固
随堂演练
2.如图:李老师家有个边长为4米的正方形院子AOBC,他想在院子里修建一个矩形水池DOEF,水池一面DO靠墙AO,另一面OE 靠墙OB,设OD = x(米),OE = y(米).
(1)若矩形水池的面积为2平方
米,则y与x的函数关系式为:
_______ ,在图中画出能建水池
的F点的位置,并用l1标记;
l1
(2)若周长为 6 米(包含两边靠墙的地方),则y与x的关系式为___________,在图中画出满足条件的水池一角F的所有位置,并用l2 标记;
(3)有没有同时满足条件(1)
(2)的水池?若有请帮忙找出
这一点,并在图中画出来;若
没有,请说明理由.
y = - x + 3
解:存在两点M( 1,2 )和N(2,1)同时满足条件(1)(2).
l1
l2
M
N
3. 如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B 处悬挂重物A,在中点O右侧用一个弹簧测力计向下拉,改变弹簧测力计与点O的距离x(cm), 观察弹簧测力计的示数y(N)的变化情况.实验数据记录如下:
综合应用
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
解:(1)y与x之间是反比例函数关系,
(2)当弹簧测力计的示数为24 N时,弹簧测力计与O点的距离是多少厘米?随着弹簧测力计与O点的距离不断减小,弹簧测力计上的示数将发生怎样的变化?
解:(2)当 y = 24 N时,由 得
示数逐渐变大.
(1)这节课你学习了哪些数学知识?
(2)我们建立反比例函数模型解决实际问题
的过程是怎样的?
课堂小结
2010年世博会期间,上海黄浦江上出现一艘白色的豪华游船在水中徜徉,高高扬起的风帆由太阳能电池板拼装而成,天气晴好之时,航行所用的动力可完全使用太阳能.图1是游船的某一部件的设计图纸.(其中∠A,
∠B,∠C是直角,DE是双
曲线的一部分,AE的长为
30 cm,AB的长为40 cm,
BC的长为60 cm)
(1)请你求出DC的长;
(2)如图2所示,有一块矩形材料ABCD,其中AB = 40 cm、AD = 60 cm,在距AD边15 cm、距CD边10 cm处有一小孔,请你判断此材料是否可用,请说明理由.
解:(1)以点 B 为坐标原点建立直角坐标系,如图所示,则 E 点坐标为(30,40),∴曲线 DE 的关系式为 ,∵D 点的横坐标为60,∴ ,∴ DC 的长为20 cm;
(2)可用,小孔坐标为(50,25),所处位置在图1图形ABCDE之外.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
数学活动
问题1:矩形的面积一定时,矩形的长和宽成什么关系?
问题2:如果把矩形的一个顶点固定,拖动这个固定顶点的对角顶点,拖动时必须保证矩形的面积不变,猜猜看,这个对角顶点的运动轨迹会是什么图象呢?
长
宽
面积不变
情境导入
下表是 10 个面积相等的矩形的长与宽,请补齐表格.
长/ cm 1 2 3 4 5
宽/ cm 2 1
活动1 探索矩形顶点的运动轨迹
10
5
6
7
8
9
10
推进新课
设∠A 为这 10 个矩形的公共角.画出这 10 个矩形,然后取∠A 的 10 个对角的顶点,并把这 10 个点用平滑的曲线顺次连接起来.
这条曲线是反比例函数图象的一支吗?为什么?
如图
1
A
x
y
5
10
5
10
1
你画
对了吗?
从表中数据可以看出,长方形的面积为 10,即 k = 10,矩形的长 y 是宽 x 的反比例函数,即
小结
1.如图,过 的图象上任意一点 P 作两坐标轴的垂线段,则图中矩形的面积 S 是定值吗?是多少?
试一试
是
S = | k |
2.如图,过 的图象上任意一点 P 作某一坐标轴的垂线段,则图中三角形的面积 S = __________
如图,取一根长 100 cm 的匀
质木杆,用细绳绑在木杆的
中点 O并将其吊起来. 在中 点O的左侧距离中点 O 25 cm处 挂一个重 9.8 N 的物体,在中 点O右侧用一个弹簧秤向下拉,
使木杆处于水平状态.改变弹
簧秤与中点 O 的距离 L(单位:cm),看弹簧秤的示数 F(单位:N)有什么变化,并填写下表:
活动2 探索力与力到支点距离的关系
以 L 的数值为横坐标,F 为纵坐标建立直角坐标系.在坐标系中描出以上表中的数对为坐标的各点,并用平滑曲线顺次连接这些点.
这条曲线是反比例函数图象的一支吗?为什么?点(50,4.9)在这条曲线上吗?
L / cm 5 10 15 20 25 30 35 40 45
F / N
杠杆的平衡条件是,作用在杠杆上的两个力的大小跟它们的力臂成反比,即
动力×动力臂 = 阻力×阻力臂
用代数式表示为
F1L1 = F2L2
式中,F1 表示动力,L1表示动力臂,F2 表示阻力,L2 表示阻力臂.从上式可以看出,欲使杠杆平衡,动力臂是阻力臂的几倍,动力就是阻力的几分之一.
杠杆的平衡条件
L / cm 5 10 15 20 25 30 35 40 45
F / N
49
24.5
16.33
12.25
9.8
8.17
7
6.125
5.44
在此活动中,弹簧秤的示数 F 是距离 L 的反比例函数,根据已知条件得
k = 9.8×25 = 245
小结
点(50,4.9)在这条曲线上.
1.如图,若点A在反比例函数 ( k ≠ 0 )的图象上,AM⊥x轴于点M,△AMO 的面积为3,则 k = _______.
– 6
基础巩固
随堂演练
2.如图:李老师家有个边长为4米的正方形院子AOBC,他想在院子里修建一个矩形水池DOEF,水池一面DO靠墙AO,另一面OE 靠墙OB,设OD = x(米),OE = y(米).
(1)若矩形水池的面积为2平方
米,则y与x的函数关系式为:
_______ ,在图中画出能建水池
的F点的位置,并用l1标记;
l1
(2)若周长为 6 米(包含两边靠墙的地方),则y与x的关系式为___________,在图中画出满足条件的水池一角F的所有位置,并用l2 标记;
(3)有没有同时满足条件(1)
(2)的水池?若有请帮忙找出
这一点,并在图中画出来;若
没有,请说明理由.
y = - x + 3
解:存在两点M( 1,2 )和N(2,1)同时满足条件(1)(2).
l1
l2
M
N
3. 如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B 处悬挂重物A,在中点O右侧用一个弹簧测力计向下拉,改变弹簧测力计与点O的距离x(cm), 观察弹簧测力计的示数y(N)的变化情况.实验数据记录如下:
综合应用
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
解:(1)y与x之间是反比例函数关系,
(2)当弹簧测力计的示数为24 N时,弹簧测力计与O点的距离是多少厘米?随着弹簧测力计与O点的距离不断减小,弹簧测力计上的示数将发生怎样的变化?
解:(2)当 y = 24 N时,由 得
示数逐渐变大.
(1)这节课你学习了哪些数学知识?
(2)我们建立反比例函数模型解决实际问题
的过程是怎样的?
课堂小结
2010年世博会期间,上海黄浦江上出现一艘白色的豪华游船在水中徜徉,高高扬起的风帆由太阳能电池板拼装而成,天气晴好之时,航行所用的动力可完全使用太阳能.图1是游船的某一部件的设计图纸.(其中∠A,
∠B,∠C是直角,DE是双
曲线的一部分,AE的长为
30 cm,AB的长为40 cm,
BC的长为60 cm)
(1)请你求出DC的长;
(2)如图2所示,有一块矩形材料ABCD,其中AB = 40 cm、AD = 60 cm,在距AD边15 cm、距CD边10 cm处有一小孔,请你判断此材料是否可用,请说明理由.
解:(1)以点 B 为坐标原点建立直角坐标系,如图所示,则 E 点坐标为(30,40),∴曲线 DE 的关系式为 ,∵D 点的横坐标为60,∴ ,∴ DC 的长为20 cm;
(2)可用,小孔坐标为(50,25),所处位置在图1图形ABCDE之外.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
