北京版八年级数学下册 一次函数的复习 教学设计(表格式)
文档属性
| 名称 | 北京版八年级数学下册 一次函数的复习 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 165.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 06:09:07 | ||
图片预览

文档简介
教 学 设 计
课题 一次函数的复习
学科 数 学 年级 八年级
教材版本 北京教育科学研究院义务教育教科书八年级下册
教材分析 本章的内容包括:变量、常量和函数的概念,函数的三种表示法,一次函数(和正比例函数)的概念、图像、性质以及应用举例.有关函数的知识是初中数学的重要内容之一,由于它是从生活中广泛的实际问题抽象出来的数学知识,所以它又是解决实际问题时被广泛应用的工具.因此,这部分知识对提高学生在生活中应用函数知识的意识以及对掌握运用函数知识的方法,都是能够培养学生应用数学知识能力的具体重要意义. 本章对一次函数的图象和性质的学习给出了研究函数的基本模式,因此掌握一次函数图象和性质的教学,对今后函数的学习有重要的示范意义.
学情分析 本章是本学期的起始章节,从开学初到现在的期末复习时隔已经三个月,大多数学生对已学过的知识都有或多或少的遗忘.在本章的学习中,学生已初步掌握了函数的概念、一次函数的图象及性质及应用,并了解了函数的三种表达方式:图象法、列表法、解析式法。在此基础上引导学生对一次函数的相关知识通过表格的形式进行梳理,以及归纳研究函数的一般方法。 进入本学期的学习后大多数学生由于性格内容,在课堂交流展示环节表现不够积极,甚至不敢举手回答问题,预设在本节课中,通过小组积分激发学生的表现欲,提高学习兴趣。
教学目标 1.学会梳理一次函数(正比例函数)的知识点,理解掌握一次函数的图象的特征和相关的性质; 2.能应用本章的基础知识熟练地解决数学问题,体会数形结合思想; 3.通过对一次函数的复习,归纳研究函数的一般方法.
教学重点 理解掌握一次函数的图象的特征和相关的性质;
教学难点 应用知识熟练地解决数学问题,体会数形结合思想;
教 学 过 程
教学环节 教师活动 学生活动 设计意图
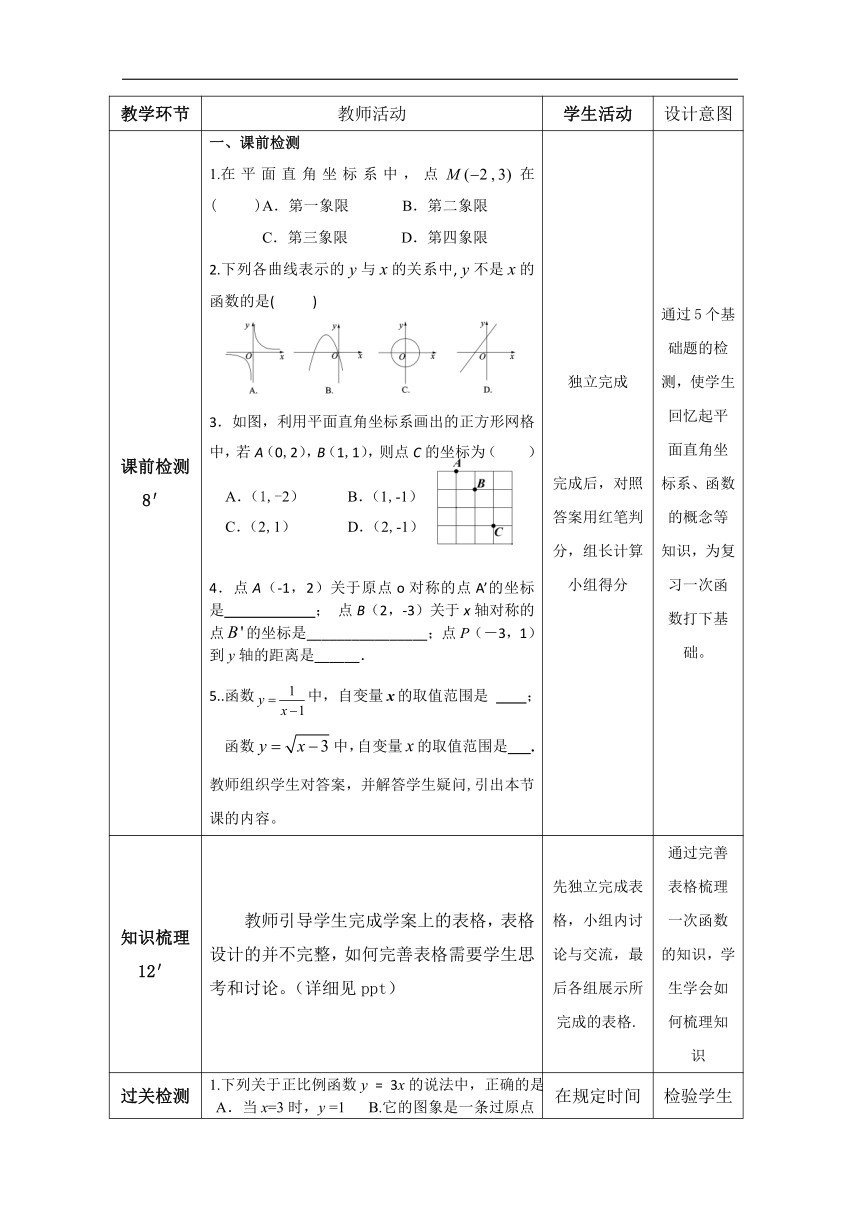
课前检测 8′ 课前检测 在平面直角坐标系中,点在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.下列各曲线表示的与的关系中,不是的函数的是( ) 3.如图,利用平面直角坐标系画出的正方形网格中,若A(0,2),B(1,1),则点C的坐标为( ) A.(1,-2) C.(2,1)B.(1,-1) D.(2,-1)
4.点A(-1,2)关于原点o对称的点A’的坐标是 ; 点B(2,-3)关于x轴对称的点的坐标是________________;点P(-3,1)到y轴的距离是______. 5..函数中,自变量的取值范围是 ; 函数中,自变量的取值范围是 . 教师组织学生对答案,并解答学生疑问,引出本节课的内容。 独立完成 完成后,对照答案用红笔判分,组长计算小组得分 通过5个基础题的检测,使学生回忆起平面直角坐标系、函数的概念等知识,为复习一次函数打下基础。
知识梳理 12′ 教师引导学生完成学案上的表格,表格设计的并不完整,如何完善表格需要学生思考和讨论。(详细见ppt) 先独立完成表格,小组内讨论与交流,最后各组展示所完成的表格. 通过完善表格梳理一次函数的知识,学生学会如何梳理知识
过关检测 20′ 1.下列关于正比例函数y = 3x的说法中,正确的是( ) A.当x=3时,y =1 B.它的图象是一条过原点的直线 C. y随x的增大而减小 D.它的图象经过第二、四象限 2.若是一次函数,则( ) A. B. C. D. 3.已知一次函数y=2x+1,则该函数的图象一定经过( ) A.第一、二、三象限 B.第一、二、四象限 C.第一、三、四象限 D.第二、三、四象限 4.已知,在平面直角坐标系xOy中,点A( -4,0 ),点B在直线y = x+2上.当A,B两点间的距离最小时,点B的坐标是( ) A.( , ) B.(, ) C.( -3,-1 ) D.(-3, ) 5.根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号: k_0,b_0 k_0,b_0 k_0,b_0 k_0,b_0 6.已知(,)、(2,)是一次函数图象上的两个点, 则 (填“>”、“<”或“=”). 7.图象经过点( 2 ,一 1 )且与直线 y = 2x + 1 平行的一次函数的表达式_________ 8.一次函数的图象经过点和x轴上一点B,且点B的横坐标是-3.求这个一次函数的表达式. 9.已知函数y=2x-4 (1)画出它的图象;(2)写出这条直线与x轴、y轴交点的坐标; (3)求这条直线与两坐标轴所围成的三角形的面积. 教师组织学生提出问题并解答问题 在规定时间内独立完成 完成后,对答案,并提出问题,学生举手解答和展示 检验学生对知识应用的情况 通过提问,学生讲解与质疑,使学生学会解题方法
课堂小结 5′ 本节课你的收获什么? 1.知识方面:一次函数知识点 2.数学思想方法:数形结合、研究函数的方法 举手发言 总结收获
板书设计 一次函数的复习
课题 一次函数的复习
学科 数 学 年级 八年级
教材版本 北京教育科学研究院义务教育教科书八年级下册
教材分析 本章的内容包括:变量、常量和函数的概念,函数的三种表示法,一次函数(和正比例函数)的概念、图像、性质以及应用举例.有关函数的知识是初中数学的重要内容之一,由于它是从生活中广泛的实际问题抽象出来的数学知识,所以它又是解决实际问题时被广泛应用的工具.因此,这部分知识对提高学生在生活中应用函数知识的意识以及对掌握运用函数知识的方法,都是能够培养学生应用数学知识能力的具体重要意义. 本章对一次函数的图象和性质的学习给出了研究函数的基本模式,因此掌握一次函数图象和性质的教学,对今后函数的学习有重要的示范意义.
学情分析 本章是本学期的起始章节,从开学初到现在的期末复习时隔已经三个月,大多数学生对已学过的知识都有或多或少的遗忘.在本章的学习中,学生已初步掌握了函数的概念、一次函数的图象及性质及应用,并了解了函数的三种表达方式:图象法、列表法、解析式法。在此基础上引导学生对一次函数的相关知识通过表格的形式进行梳理,以及归纳研究函数的一般方法。 进入本学期的学习后大多数学生由于性格内容,在课堂交流展示环节表现不够积极,甚至不敢举手回答问题,预设在本节课中,通过小组积分激发学生的表现欲,提高学习兴趣。
教学目标 1.学会梳理一次函数(正比例函数)的知识点,理解掌握一次函数的图象的特征和相关的性质; 2.能应用本章的基础知识熟练地解决数学问题,体会数形结合思想; 3.通过对一次函数的复习,归纳研究函数的一般方法.
教学重点 理解掌握一次函数的图象的特征和相关的性质;
教学难点 应用知识熟练地解决数学问题,体会数形结合思想;
教 学 过 程
教学环节 教师活动 学生活动 设计意图
课前检测 8′ 课前检测 在平面直角坐标系中,点在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.下列各曲线表示的与的关系中,不是的函数的是( ) 3.如图,利用平面直角坐标系画出的正方形网格中,若A(0,2),B(1,1),则点C的坐标为( ) A.(1,-2) C.(2,1)B.(1,-1) D.(2,-1)
4.点A(-1,2)关于原点o对称的点A’的坐标是 ; 点B(2,-3)关于x轴对称的点的坐标是________________;点P(-3,1)到y轴的距离是______. 5..函数中,自变量的取值范围是 ; 函数中,自变量的取值范围是 . 教师组织学生对答案,并解答学生疑问,引出本节课的内容。 独立完成 完成后,对照答案用红笔判分,组长计算小组得分 通过5个基础题的检测,使学生回忆起平面直角坐标系、函数的概念等知识,为复习一次函数打下基础。
知识梳理 12′ 教师引导学生完成学案上的表格,表格设计的并不完整,如何完善表格需要学生思考和讨论。(详细见ppt) 先独立完成表格,小组内讨论与交流,最后各组展示所完成的表格. 通过完善表格梳理一次函数的知识,学生学会如何梳理知识
过关检测 20′ 1.下列关于正比例函数y = 3x的说法中,正确的是( ) A.当x=3时,y =1 B.它的图象是一条过原点的直线 C. y随x的增大而减小 D.它的图象经过第二、四象限 2.若是一次函数,则( ) A. B. C. D. 3.已知一次函数y=2x+1,则该函数的图象一定经过( ) A.第一、二、三象限 B.第一、二、四象限 C.第一、三、四象限 D.第二、三、四象限 4.已知,在平面直角坐标系xOy中,点A( -4,0 ),点B在直线y = x+2上.当A,B两点间的距离最小时,点B的坐标是( ) A.( , ) B.(, ) C.( -3,-1 ) D.(-3, ) 5.根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号: k_0,b_0 k_0,b_0 k_0,b_0 k_0,b_0 6.已知(,)、(2,)是一次函数图象上的两个点, 则 (填“>”、“<”或“=”). 7.图象经过点( 2 ,一 1 )且与直线 y = 2x + 1 平行的一次函数的表达式_________ 8.一次函数的图象经过点和x轴上一点B,且点B的横坐标是-3.求这个一次函数的表达式. 9.已知函数y=2x-4 (1)画出它的图象;(2)写出这条直线与x轴、y轴交点的坐标; (3)求这条直线与两坐标轴所围成的三角形的面积. 教师组织学生提出问题并解答问题 在规定时间内独立完成 完成后,对答案,并提出问题,学生举手解答和展示 检验学生对知识应用的情况 通过提问,学生讲解与质疑,使学生学会解题方法
课堂小结 5′ 本节课你的收获什么? 1.知识方面:一次函数知识点 2.数学思想方法:数形结合、研究函数的方法 举手发言 总结收获
板书设计 一次函数的复习
同课章节目录
