鲁教版(五四制)数学七年级上册第四章综合素质评价卷(word版、含答案)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册第四章综合素质评价卷(word版、含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 185.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 11:56:11 | ||
图片预览



文档简介
第四章综合素质评价
一、选择题(每题3分,共36分)
1.的值是( )
A.1 B.-1 C.3 D.-3
2.下列各数中,是无理数的是( )
A.3.141 5 B. C. D.
3.下列各数中,绝对值最小的数是( )
A.-5 B. C.-1 D.
4.下列说法中,正确的是( )
①-64的立方根是-4;② 49的算术平方根是7;
③-的平方根为±;④ 的平方根是.
A.①② B.②③ C.③④ D.②④
5.下列算式中正确的是( )
A.=±5 B.±=3 C.=-2 D.=-2
6.实数a,b在数轴上对应点的位置如图所示,下列判断正确的是( )
A.|a|<1 B.ab>0 C.a+b>0 D.1-a>1
7.已知+|b-4|=0,则的平方根是( )
A. B.± C.± D.
8.若a2=9,=-2,则a+b=( )
A.-5 B.-11 C.-5或-11 D.±5或±11
9.设n为正整数,且n<<n+1,则n的值为( )
A.4 B.5 C.6 D.7
10.已知x-2的平方根是±2,2x+y+7的立方根是3,则x+y的值为( )
A.11 B.12 C.13 D.14
11.已知实数x,y满足y=,则的值为( )
A.0 B. C. D.5
12.已知min{a,b,c}表示取三个数中最小的那个数.例如min{|-2|,(-2)2,(-2)3}=-8,当min{,x2,x}=时,x的值为( )
A. B. C. D.
二、填空题(每题3分,共18分)
13.的相反数是________;-的绝对值是________.
14.比较大小:________(填“>”“<”或“=”).
15.一个正方体木块的体积为1 000 cm3,现要把它锯成64个同样大小的小正方体木块,则每个小正方体木块的棱长为________cm.
16.已知(2a+b)2与互为相反数,则ba=________.
17.设m,n分别是-1的整数部分和小数部分,则2m-n=________.
18.任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[]=1.现对72进行如下操作:72[]=8[]=2[]=1,这样对72只需进行3次操作即可变为1,类似地,对81只需进行________次操作即可变为1;只需进行3次操作即可变为1的所有正整数中,最大的是________.
三、解答题(19~21题每题8分,25题12分,其余每题10分,共66分)
19.把下列各数写在相应的集合中:
-,,0.3,,,,0,0.575 775 777 5…(相邻两个5之间7的个数逐次加1).
(1)正实数集合:{ …};
(2)负实数集合:{ …};
(3)有理数集合:{ …};
(4)无理数集合:{ …}.
20.(1)已知9(x+1)2=4,求x的值;
(2)已知8(x-1)3=-,求x的值.
21.已知一个数的算术平方根为2m-6,平方根为±(m-1),求m的值.
22.如图是一个无理数筛选器的工作流程图.
(1)当x为16时,y的值为________.
(2)是否存在输入有意义的x值后,却输不出y值的情况?如果存在,写出所有满足要求的x值;如果不存在,请说明理由.
(3)当输出的y值是时,判断输入的x值是否唯一,如果不唯一,请直接写出其中的两个.
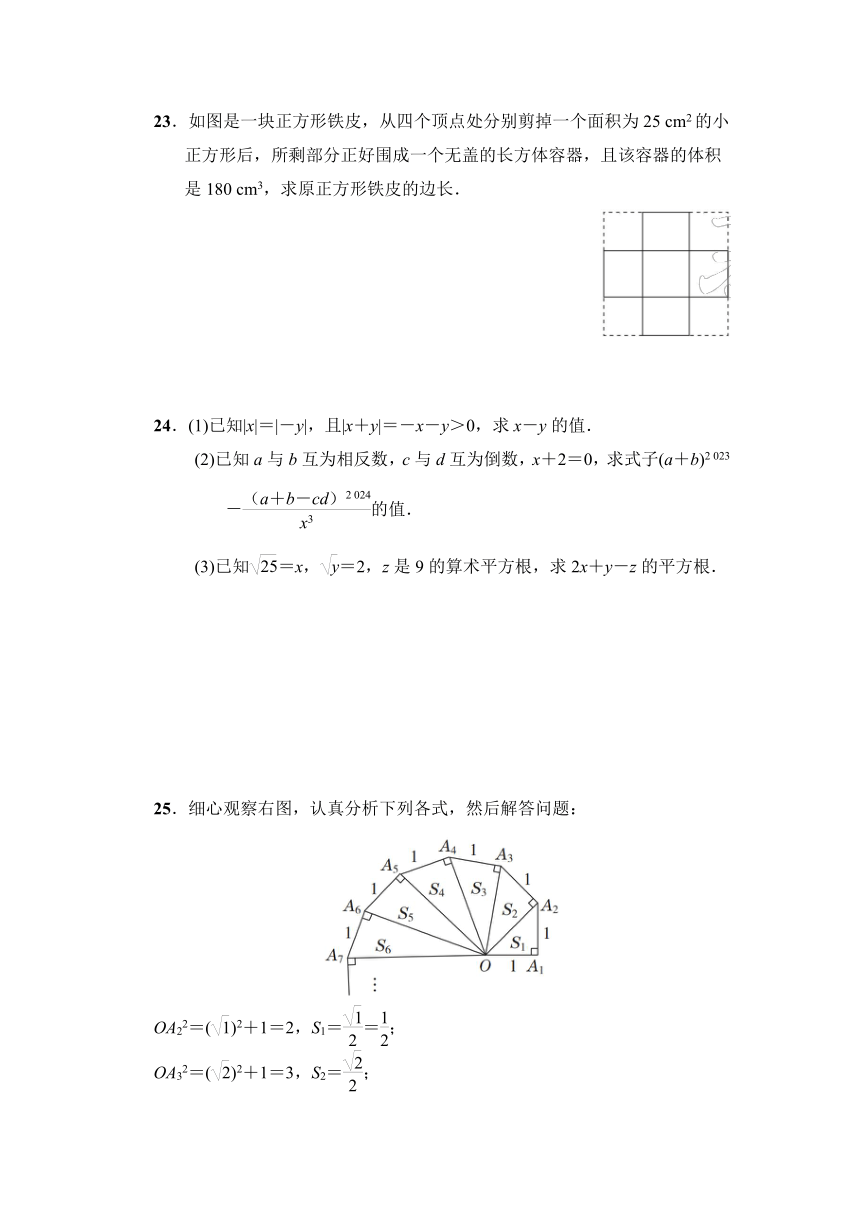
23.如图是一块正方形铁皮,从四个顶点处分别剪掉一个面积为25 cm2的小正方形后,所剩部分正好围成一个无盖的长方体容器,且该容器的体积是180 cm3,求原正方形铁皮的边长.
24.(1)已知|x|=|-y|,且|x+y|=-x-y>0,求x-y的值.
(2)已知a与b互为相反数,c与d互为倒数,x+2=0,求式子(a+b)2 023-的值.
(3)已知=x,=2,z是9的算术平方根,求2x+y-z的平方根.
25.细心观察右图,认真分析下列各式,然后解答问题:
OA22=()2+1=2,S1==;
OA32=()2+1=3,S2=;
OA42=()2+1=4,S3=;
…
(1)用含n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求出S12+S22+S32+…+S102的值.
答案
一、1.B 2.D 3.B 4.A 5.D 6.D
7.B 8.C 9.C
10.D 因为x-2的平方根是±2,2x+y+7的立方根是3,
所以x-2=4,2x+y+7=27.
解得x=6,y=8.
所以x+y=6+8=14.
11.D 由题意得x2-16=0,
且x≠4,所以x=-4,所以y=-3,所以==5.
12.C 当=时,x=,x<,不合题意.
当x2=时,x=±,当x=-时,无意义,舍去;
当x=时,=,x2当x=时,x2=,x2二、13.-; 14.> 15.
16.16 根据题意得(2a+b)2+=0,
所以2a+b=0,3b+12=0.
所以a=2,b=-4.
所以ba= (-4)2=16.
17.1- 点拨:由题意知-1的整数部分m=0,小数部分n=-1,则2m-n=0-(-1)=1-.
18.3;255
三、19.解:(1)正实数集合:{,0.3,,,0.575 775 777 5…(相邻两个5之间7的个数逐次加1),…};
(2)负实数集合:{-,,…};
(3)有理数集合:{-,0.3,,,0,…};
(4)无理数集合:{,,0.575 775 777 5…(相邻两个5之间7的个数逐次加1),…}.
20.解:(1)方程整理得(x+1)2=,
开平方得x+1=±,
解得x=-或x=-.
(2)方程整理得(x-1)3=-,
开立方得x-1=-,
解得x=-.
21.解:当m-1≥0,即m≥1时,
2m-6=m-1,
解得m=5;
当-(m-1)>0,即m<1时,
2m-6=-(m-1),
解得m=(不合题意,舍去).
所以m=5.
22.解:(1)
(2)存在.
因为0,1的算术平方根分别是0,1,一定是有理数,
所以当x=0,1时,始终输不出y值.
(3)输入的x值不唯一.x=3或x=9.
23.解:因为从四个顶点处分别剪掉一个面积为25 cm2的小正方形,
所以剪掉的小正方形边长为5 cm.
设原正方形铁皮的边长为x cm,
由题意可得5(x-10)2=180,
所以(x-10)2=36,
开平方得x-10=±6,
解得x=16或x=4.
因为x-10>0,即x>10,所以x=16.
所以原正方形铁皮的边长为16 cm.
24.解:(1)因为|x|=|-y|,
所以x=y或x=-y.
因为|x+y|=-x-y>0,
所以x+y<0.
所以x=y.所以x-y=0.
(2)因为a与b互为相反数,
所以a+b=0.
因为c与d互为倒数,所以cd=1.
因为x+2=0,所以x=-2.
所以(a+b)2 023-=0-=.
(3)因为=x,所以x=5.
因为=2,所以y=4.
因为z是9的算术平方根,
所以z=3,
所以2x+y-z=10+4-3=11,
所以2x+y-z的平方根是±.
25.解:(1)由题意得OAn+12=()2+1=n+1,Sn=.
(2)由(1)知OA102=()2+12=10,
所以OA10=.
(3)S12+S22+S32+…+S102
=+++…+
=+++…+
=×(1+2+3+…+10)
=.
一、选择题(每题3分,共36分)
1.的值是( )
A.1 B.-1 C.3 D.-3
2.下列各数中,是无理数的是( )
A.3.141 5 B. C. D.
3.下列各数中,绝对值最小的数是( )
A.-5 B. C.-1 D.
4.下列说法中,正确的是( )
①-64的立方根是-4;② 49的算术平方根是7;
③-的平方根为±;④ 的平方根是.
A.①② B.②③ C.③④ D.②④
5.下列算式中正确的是( )
A.=±5 B.±=3 C.=-2 D.=-2
6.实数a,b在数轴上对应点的位置如图所示,下列判断正确的是( )
A.|a|<1 B.ab>0 C.a+b>0 D.1-a>1
7.已知+|b-4|=0,则的平方根是( )
A. B.± C.± D.
8.若a2=9,=-2,则a+b=( )
A.-5 B.-11 C.-5或-11 D.±5或±11
9.设n为正整数,且n<<n+1,则n的值为( )
A.4 B.5 C.6 D.7
10.已知x-2的平方根是±2,2x+y+7的立方根是3,则x+y的值为( )
A.11 B.12 C.13 D.14
11.已知实数x,y满足y=,则的值为( )
A.0 B. C. D.5
12.已知min{a,b,c}表示取三个数中最小的那个数.例如min{|-2|,(-2)2,(-2)3}=-8,当min{,x2,x}=时,x的值为( )
A. B. C. D.
二、填空题(每题3分,共18分)
13.的相反数是________;-的绝对值是________.
14.比较大小:________(填“>”“<”或“=”).
15.一个正方体木块的体积为1 000 cm3,现要把它锯成64个同样大小的小正方体木块,则每个小正方体木块的棱长为________cm.
16.已知(2a+b)2与互为相反数,则ba=________.
17.设m,n分别是-1的整数部分和小数部分,则2m-n=________.
18.任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[]=1.现对72进行如下操作:72[]=8[]=2[]=1,这样对72只需进行3次操作即可变为1,类似地,对81只需进行________次操作即可变为1;只需进行3次操作即可变为1的所有正整数中,最大的是________.
三、解答题(19~21题每题8分,25题12分,其余每题10分,共66分)
19.把下列各数写在相应的集合中:
-,,0.3,,,,0,0.575 775 777 5…(相邻两个5之间7的个数逐次加1).
(1)正实数集合:{ …};
(2)负实数集合:{ …};
(3)有理数集合:{ …};
(4)无理数集合:{ …}.
20.(1)已知9(x+1)2=4,求x的值;
(2)已知8(x-1)3=-,求x的值.
21.已知一个数的算术平方根为2m-6,平方根为±(m-1),求m的值.
22.如图是一个无理数筛选器的工作流程图.
(1)当x为16时,y的值为________.
(2)是否存在输入有意义的x值后,却输不出y值的情况?如果存在,写出所有满足要求的x值;如果不存在,请说明理由.
(3)当输出的y值是时,判断输入的x值是否唯一,如果不唯一,请直接写出其中的两个.
23.如图是一块正方形铁皮,从四个顶点处分别剪掉一个面积为25 cm2的小正方形后,所剩部分正好围成一个无盖的长方体容器,且该容器的体积是180 cm3,求原正方形铁皮的边长.
24.(1)已知|x|=|-y|,且|x+y|=-x-y>0,求x-y的值.
(2)已知a与b互为相反数,c与d互为倒数,x+2=0,求式子(a+b)2 023-的值.
(3)已知=x,=2,z是9的算术平方根,求2x+y-z的平方根.
25.细心观察右图,认真分析下列各式,然后解答问题:
OA22=()2+1=2,S1==;
OA32=()2+1=3,S2=;
OA42=()2+1=4,S3=;
…
(1)用含n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求出S12+S22+S32+…+S102的值.
答案
一、1.B 2.D 3.B 4.A 5.D 6.D
7.B 8.C 9.C
10.D 因为x-2的平方根是±2,2x+y+7的立方根是3,
所以x-2=4,2x+y+7=27.
解得x=6,y=8.
所以x+y=6+8=14.
11.D 由题意得x2-16=0,
且x≠4,所以x=-4,所以y=-3,所以==5.
12.C 当=时,x=,x<,不合题意.
当x2=时,x=±,当x=-时,无意义,舍去;
当x=时,=,x2
16.16 根据题意得(2a+b)2+=0,
所以2a+b=0,3b+12=0.
所以a=2,b=-4.
所以ba= (-4)2=16.
17.1- 点拨:由题意知-1的整数部分m=0,小数部分n=-1,则2m-n=0-(-1)=1-.
18.3;255
三、19.解:(1)正实数集合:{,0.3,,,0.575 775 777 5…(相邻两个5之间7的个数逐次加1),…};
(2)负实数集合:{-,,…};
(3)有理数集合:{-,0.3,,,0,…};
(4)无理数集合:{,,0.575 775 777 5…(相邻两个5之间7的个数逐次加1),…}.
20.解:(1)方程整理得(x+1)2=,
开平方得x+1=±,
解得x=-或x=-.
(2)方程整理得(x-1)3=-,
开立方得x-1=-,
解得x=-.
21.解:当m-1≥0,即m≥1时,
2m-6=m-1,
解得m=5;
当-(m-1)>0,即m<1时,
2m-6=-(m-1),
解得m=(不合题意,舍去).
所以m=5.
22.解:(1)
(2)存在.
因为0,1的算术平方根分别是0,1,一定是有理数,
所以当x=0,1时,始终输不出y值.
(3)输入的x值不唯一.x=3或x=9.
23.解:因为从四个顶点处分别剪掉一个面积为25 cm2的小正方形,
所以剪掉的小正方形边长为5 cm.
设原正方形铁皮的边长为x cm,
由题意可得5(x-10)2=180,
所以(x-10)2=36,
开平方得x-10=±6,
解得x=16或x=4.
因为x-10>0,即x>10,所以x=16.
所以原正方形铁皮的边长为16 cm.
24.解:(1)因为|x|=|-y|,
所以x=y或x=-y.
因为|x+y|=-x-y>0,
所以x+y<0.
所以x=y.所以x-y=0.
(2)因为a与b互为相反数,
所以a+b=0.
因为c与d互为倒数,所以cd=1.
因为x+2=0,所以x=-2.
所以(a+b)2 023-=0-=.
(3)因为=x,所以x=5.
因为=2,所以y=4.
因为z是9的算术平方根,
所以z=3,
所以2x+y-z=10+4-3=11,
所以2x+y-z的平方根是±.
25.解:(1)由题意得OAn+12=()2+1=n+1,Sn=.
(2)由(1)知OA102=()2+12=10,
所以OA10=.
(3)S12+S22+S32+…+S102
=+++…+
=+++…+
=×(1+2+3+…+10)
=.
