苏科版数学八年级下册9.3 第3课时 平行四边形的判定(2)同步课件(共13张PPT)
文档属性
| 名称 | 苏科版数学八年级下册9.3 第3课时 平行四边形的判定(2)同步课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 200.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 06:52:33 | ||
图片预览



文档简介
(共13张PPT)
第九章 中心对称图形——平行四边形
9.3 第3课时 平行四边形的判定(2)
上节课我们学过平行四边形有哪些判定方法?
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
从对角线看:
知识回顾
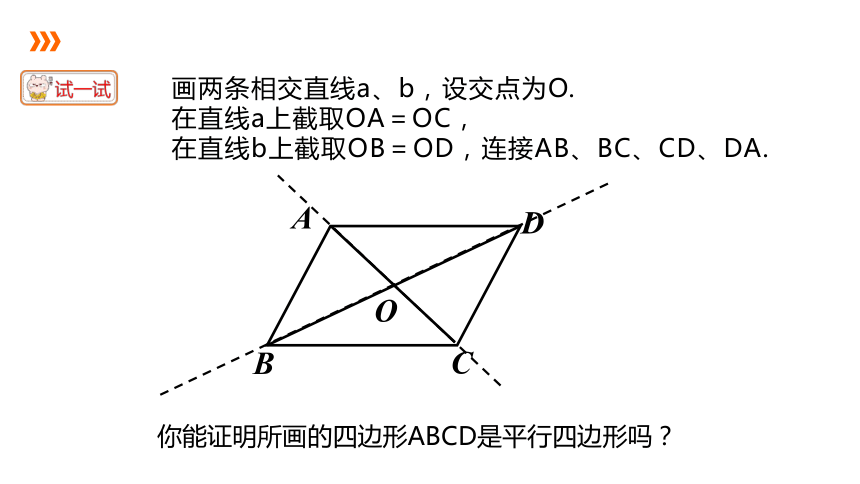
画两条相交直线a、b,设交点为O.
在直线a上截取OA=OC,
在直线b上截取OB=OD,连接AB、BC、CD、DA.
你能证明所画的四边形ABCD是平行四边形吗?
A
B
C
D
O
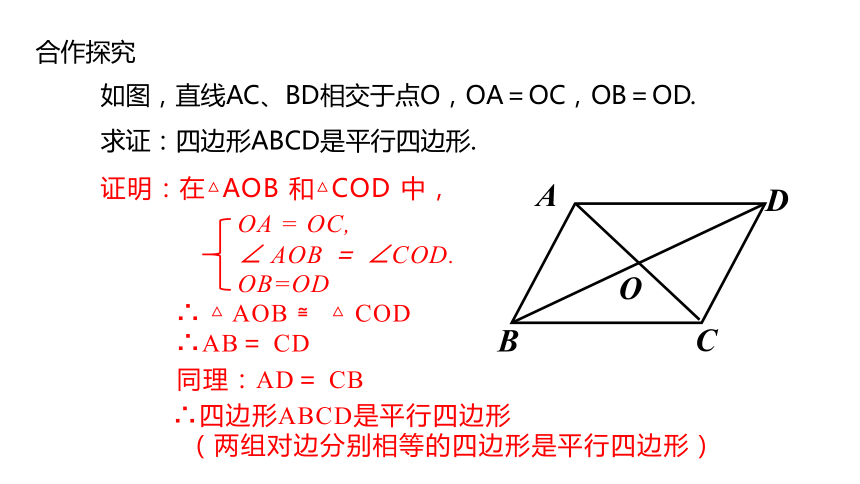
合作探究
如图,直线AC、BD相交于点O,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
A
B
C
D
O
证明:在△AOB 和△COD 中,
OA = OC,
∠ AOB = ∠COD.
OB=OD
∴ △ AOB ≌ △ COD
∴AB= CD
同理:AD= CB
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
定理:对角线互相平分的四边形是平行四边形.
几何语言:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
A
B
C
D
O
归纳总结
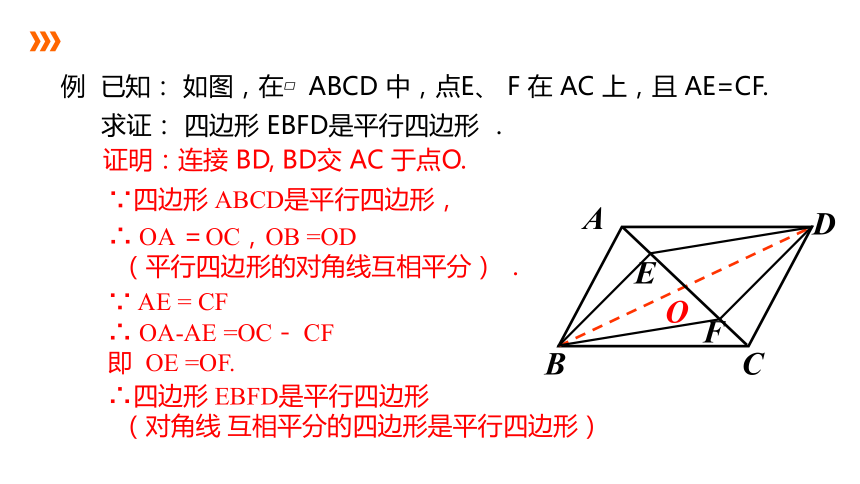
例 已知: 如图,在 ABCD 中,点E、 F 在 AC 上,且 AE=CF.
求证: 四边形 EBFD是平行四边形 .
证明:连接 BD, BD交 AC 于点O.
∵四边形 ABCD是平行四边形,
∴ OA =OC,OB =OD
(平行四边形的对角线互相平分) .
∵ AE = CF
∴ OA-AE =OC- CF
即 OE =OF.
∴四边形 EBFD是平行四边形
(对角线 互相平分的四边形是平行四边形)
A
B
C
D
O
E
F
证明:假设四边形ABCD是平行四边形,
那么OA= OC, OB=OD,
这与条件OB=OD矛盾
所以四边形 ABCD 不是平行四边形.
如图,如果OA= OC, OB ≠ OD,
那么四边形ABCD不是平行四边形.试证明这个结论
反证法
先提出与结论相反的假设, 然后由这个 “假设” 出发推导出矛盾的结果, 说明假设是错误的, 因而命题的结论成立. 这种证明的方法称为反证法(reduction to absurdity).
1、已知:如图,在 ABCD中,对角线AC、BD 相交于点O,E、F、G、H分别是OA、OB、OC、OD的中点.
求证:四边形EFGH是平行四边形.
证明:四边形 ABCD是平行四边形.
∴ OA =OC,OB =OD
(平行四边形的对角线互相平分) .
∴ OE =OG、OF=OH
∴四边形 EFGH是平行四边形
(对角线互相平分的四边形是平行四边形)
5. 如图,AC是平行四边形ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,四边形BMDN是平行四边形吗?
说说你的理由.
解:四边形BMDN是平行四边形.
理由如下:连接BD交AC于O.
∵BM⊥AC于M,DN⊥AC于N,
∴∠AND=∠CMB=90°.
∵四边形ABCD是平行四边形,
∴OB=OD,AO=CO,AD=BC,AD∥BC,
∴∠DAN=∠BCM,
∴△ADN≌△CBM,∴AN=CM,
∴OA-AN=OC-CM,即ON=OM,
∴四边形BMDN是平行四边形.
O
课堂小结
平行四边形的判定
定义法:两组对边分别平行的四边形是平行四边形
定理1:一组对边平行且相等的四边形是平行四边形
定理2:两组对边分别相等的四边形是平行四边形
定理3:对角线互相平分的四边形是平行四边形
第九章 中心对称图形——平行四边形
9.3 第3课时 平行四边形的判定(2)
上节课我们学过平行四边形有哪些判定方法?
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
从对角线看:
知识回顾
画两条相交直线a、b,设交点为O.
在直线a上截取OA=OC,
在直线b上截取OB=OD,连接AB、BC、CD、DA.
你能证明所画的四边形ABCD是平行四边形吗?
A
B
C
D
O
合作探究
如图,直线AC、BD相交于点O,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
A
B
C
D
O
证明:在△AOB 和△COD 中,
OA = OC,
∠ AOB = ∠COD.
OB=OD
∴ △ AOB ≌ △ COD
∴AB= CD
同理:AD= CB
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
定理:对角线互相平分的四边形是平行四边形.
几何语言:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
A
B
C
D
O
归纳总结
例 已知: 如图,在 ABCD 中,点E、 F 在 AC 上,且 AE=CF.
求证: 四边形 EBFD是平行四边形 .
证明:连接 BD, BD交 AC 于点O.
∵四边形 ABCD是平行四边形,
∴ OA =OC,OB =OD
(平行四边形的对角线互相平分) .
∵ AE = CF
∴ OA-AE =OC- CF
即 OE =OF.
∴四边形 EBFD是平行四边形
(对角线 互相平分的四边形是平行四边形)
A
B
C
D
O
E
F
证明:假设四边形ABCD是平行四边形,
那么OA= OC, OB=OD,
这与条件OB=OD矛盾
所以四边形 ABCD 不是平行四边形.
如图,如果OA= OC, OB ≠ OD,
那么四边形ABCD不是平行四边形.试证明这个结论
反证法
先提出与结论相反的假设, 然后由这个 “假设” 出发推导出矛盾的结果, 说明假设是错误的, 因而命题的结论成立. 这种证明的方法称为反证法(reduction to absurdity).
1、已知:如图,在 ABCD中,对角线AC、BD 相交于点O,E、F、G、H分别是OA、OB、OC、OD的中点.
求证:四边形EFGH是平行四边形.
证明:四边形 ABCD是平行四边形.
∴ OA =OC,OB =OD
(平行四边形的对角线互相平分) .
∴ OE =OG、OF=OH
∴四边形 EFGH是平行四边形
(对角线互相平分的四边形是平行四边形)
5. 如图,AC是平行四边形ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,四边形BMDN是平行四边形吗?
说说你的理由.
解:四边形BMDN是平行四边形.
理由如下:连接BD交AC于O.
∵BM⊥AC于M,DN⊥AC于N,
∴∠AND=∠CMB=90°.
∵四边形ABCD是平行四边形,
∴OB=OD,AO=CO,AD=BC,AD∥BC,
∴∠DAN=∠BCM,
∴△ADN≌△CBM,∴AN=CM,
∴OA-AN=OC-CM,即ON=OM,
∴四边形BMDN是平行四边形.
O
课堂小结
平行四边形的判定
定义法:两组对边分别平行的四边形是平行四边形
定理1:一组对边平行且相等的四边形是平行四边形
定理2:两组对边分别相等的四边形是平行四边形
定理3:对角线互相平分的四边形是平行四边形
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
