苏科版数学八年级下册9.4 第1课时 矩形及其性质 同步课件(共16张PPT)
文档属性
| 名称 | 苏科版数学八年级下册9.4 第1课时 矩形及其性质 同步课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 215.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 06:55:03 | ||
图片预览

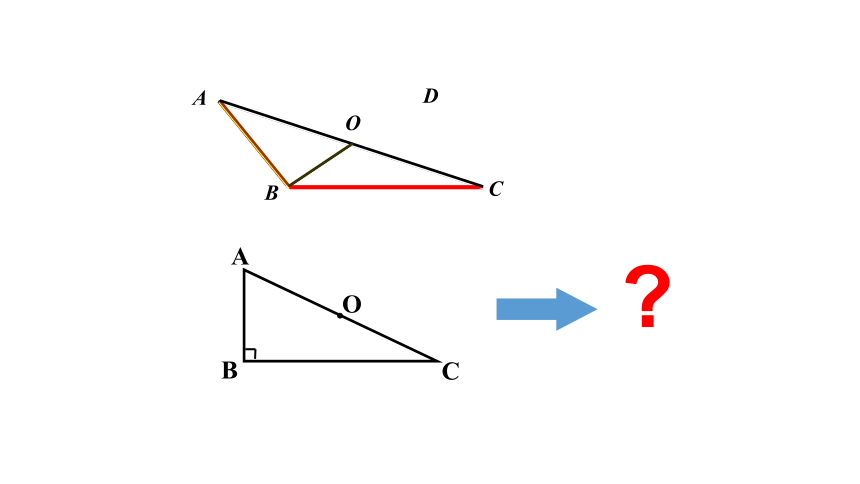

文档简介
(共16张PPT)
第九章 中心对称图形——平行四边形
9.4 第1课时 矩形及其性质
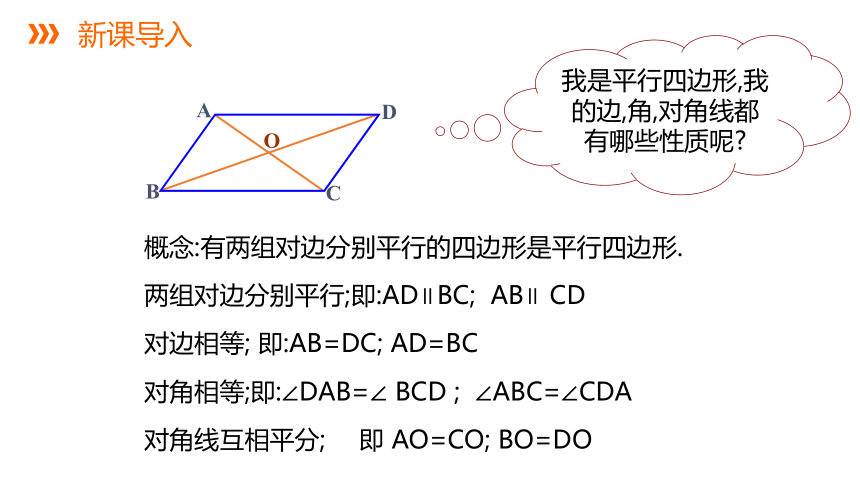
我是平行四边形,我的边,角,对角线都有哪些性质呢
概念:有两组对边分别平行的四边形是平行四边形.
O
A
B
D
C
两组对边分别平行;即:AD∥BC; AB∥ CD
对边相等; 即:AB=DC; AD=BC
对角相等;即:∠DAB=∠ BCD ; ∠ABC=∠CDA
对角线互相平分;
即 AO=CO; BO=DO
新课导入
A
B
C
D
O
A
B
C
O
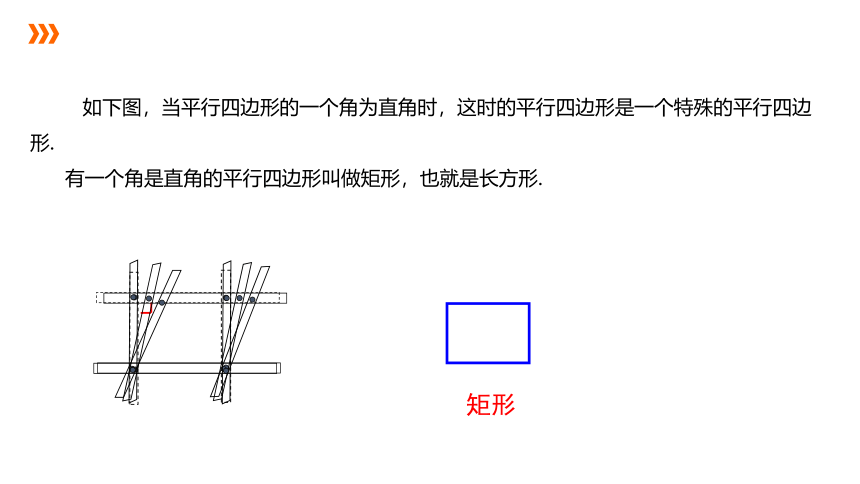
如下图,当平行四边形的一个角为直角时,这时的平行四边形是一个特殊的平行四边形.
有一个角是直角的平行四边形叫做矩形,也就是长方形.
矩形
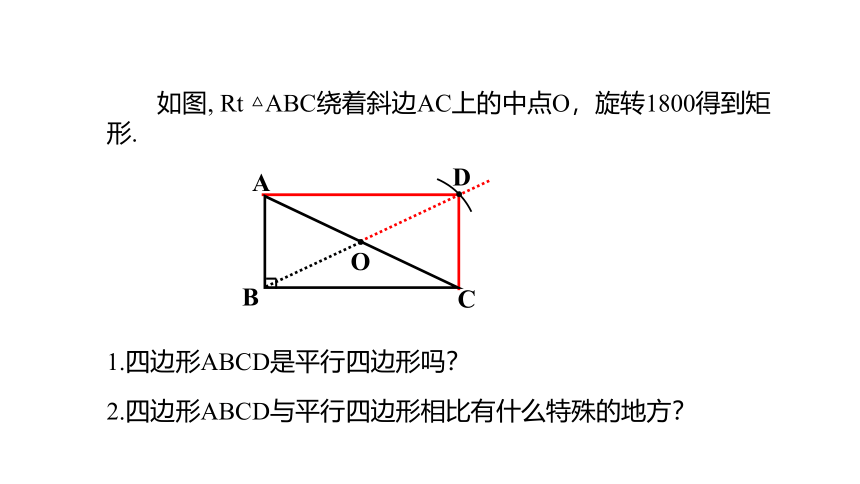
如图, Rt △ABC绕着斜边AC上的中点O,旋转1800得到矩形.
D
A
B
C
O
1.四边形ABCD是平行四边形吗?
2.四边形ABCD与平行四边形相比有什么特殊的地方?
木门
纸张
电脑显示屏
生活中的矩形图
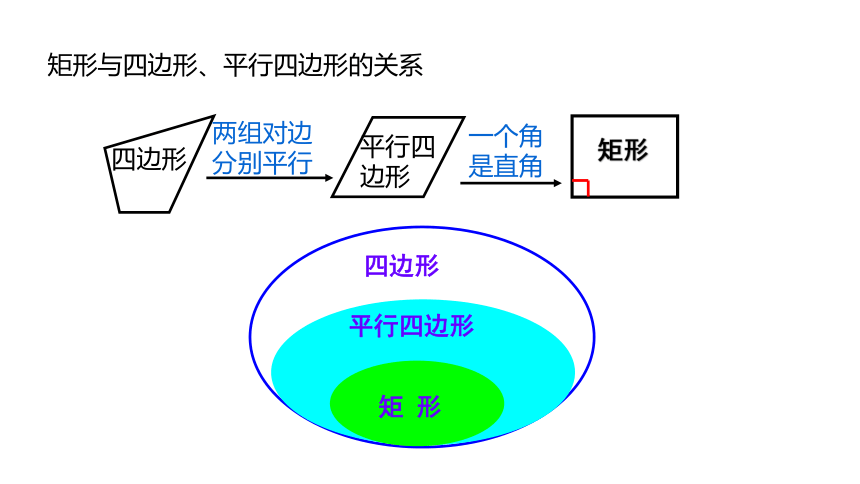
矩形与四边形、平行四边形的关系
四边形
平行四
边形
两组对边
分别平行
一个角
是直角
矩形
四边形
平行四边形
矩 形
矩形的性质定理
┒
┒
┒
┒
A
B
C
D
O
矩形的四个角都是直角
矩形的对角线相等
A
B
C
D
O
矩形性质证明:
A
B
D
C
O
┒
┒
┒
┒
∵∠B=90o
∠A+∠B=180o
∴∠A=90o
∵∠A= ∠C
∠B= ∠D
∴∠C=∠D=90o
∵AB=DC
BC=CB
∠ABC=∠DCB=90o
∴△ABC≌ △DCB(SAS)
∴AC=BD
矩形是中心对称图形,对称中心是对角线的交点。
矩形是轴对称图形,一共有2条对称轴。
矩形是中心对称图形吗?是轴对称图形吗?
A
B
C
D
O
想一想
例1 矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4,
求AC的长.
A
B
C
D
O
∴ ∠OAB = ∠OBA= ∠AOB = 60°,
解:∵四边形ABCD是矩形,
∴AC=DB. (矩形的对角线相等)
又∵OA= AC,OB= BD,
(矩形的对角线互相平分)
∴OA=OB.
又∵∠AOB =60°,
∴ AC=2OA =8.
∴ OA=AB = OB =4.(等角对等边)
例2 如图, 矩形ABCD对角线AC,BD相交于点O,且AC=2AB ,求证: △AOB是等边三角形.
证明:∵四边形ABCD是矩形,
∴AC=BD,OA= OB ,OB= BD.
又 AC=2AB ,即AB= AC,
∴OA=OB= AB.
∴△AOB是等边三角形.
4.下列性质中,矩形不一定具有的是( )
A、对角线相等 B、 四个角都相等
C、对角线垂直 D、是轴对称图形
1.矩形的定义中有两个条件:一是____________,二是_________________。
2.有一个角是直角的四边形是矩形。( )
3.矩形的对角线互相平分。( )
平行四边形
有一个角是直角
√
×
C
5.矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形,( )个直角三角形。
(A)2 (B)4 (C)6 (D)8
B
B
O
A
B
D
C
6. 如图,在矩形ABCD中,BF=CE.求证:AE=DF.
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB.
∵BF=CE,
∴BF+EF=CE+EF,
即BE=CF,
∴△ABE≌△DCF(S.A.S.),
∴AE=DF.
矩形的相关概念及性质
具有平行四边行的一切性质
1.四个内角都是直角,
2.两条对角线相等
3.是轴对称图形,有两条对称轴
有一个角是直角的平行四边形叫做矩形
概念
一般性质
特有性质
课堂小结
第九章 中心对称图形——平行四边形
9.4 第1课时 矩形及其性质
我是平行四边形,我的边,角,对角线都有哪些性质呢
概念:有两组对边分别平行的四边形是平行四边形.
O
A
B
D
C
两组对边分别平行;即:AD∥BC; AB∥ CD
对边相等; 即:AB=DC; AD=BC
对角相等;即:∠DAB=∠ BCD ; ∠ABC=∠CDA
对角线互相平分;
即 AO=CO; BO=DO
新课导入
A
B
C
D
O
A
B
C
O
如下图,当平行四边形的一个角为直角时,这时的平行四边形是一个特殊的平行四边形.
有一个角是直角的平行四边形叫做矩形,也就是长方形.
矩形
如图, Rt △ABC绕着斜边AC上的中点O,旋转1800得到矩形.
D
A
B
C
O
1.四边形ABCD是平行四边形吗?
2.四边形ABCD与平行四边形相比有什么特殊的地方?
木门
纸张
电脑显示屏
生活中的矩形图
矩形与四边形、平行四边形的关系
四边形
平行四
边形
两组对边
分别平行
一个角
是直角
矩形
四边形
平行四边形
矩 形
矩形的性质定理
┒
┒
┒
┒
A
B
C
D
O
矩形的四个角都是直角
矩形的对角线相等
A
B
C
D
O
矩形性质证明:
A
B
D
C
O
┒
┒
┒
┒
∵∠B=90o
∠A+∠B=180o
∴∠A=90o
∵∠A= ∠C
∠B= ∠D
∴∠C=∠D=90o
∵AB=DC
BC=CB
∠ABC=∠DCB=90o
∴△ABC≌ △DCB(SAS)
∴AC=BD
矩形是中心对称图形,对称中心是对角线的交点。
矩形是轴对称图形,一共有2条对称轴。
矩形是中心对称图形吗?是轴对称图形吗?
A
B
C
D
O
想一想
例1 矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4,
求AC的长.
A
B
C
D
O
∴ ∠OAB = ∠OBA= ∠AOB = 60°,
解:∵四边形ABCD是矩形,
∴AC=DB. (矩形的对角线相等)
又∵OA= AC,OB= BD,
(矩形的对角线互相平分)
∴OA=OB.
又∵∠AOB =60°,
∴ AC=2OA =8.
∴ OA=AB = OB =4.(等角对等边)
例2 如图, 矩形ABCD对角线AC,BD相交于点O,且AC=2AB ,求证: △AOB是等边三角形.
证明:∵四边形ABCD是矩形,
∴AC=BD,OA= OB ,OB= BD.
又 AC=2AB ,即AB= AC,
∴OA=OB= AB.
∴△AOB是等边三角形.
4.下列性质中,矩形不一定具有的是( )
A、对角线相等 B、 四个角都相等
C、对角线垂直 D、是轴对称图形
1.矩形的定义中有两个条件:一是____________,二是_________________。
2.有一个角是直角的四边形是矩形。( )
3.矩形的对角线互相平分。( )
平行四边形
有一个角是直角
√
×
C
5.矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形,( )个直角三角形。
(A)2 (B)4 (C)6 (D)8
B
B
O
A
B
D
C
6. 如图,在矩形ABCD中,BF=CE.求证:AE=DF.
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB.
∵BF=CE,
∴BF+EF=CE+EF,
即BE=CF,
∴△ABE≌△DCF(S.A.S.),
∴AE=DF.
矩形的相关概念及性质
具有平行四边行的一切性质
1.四个内角都是直角,
2.两条对角线相等
3.是轴对称图形,有两条对称轴
有一个角是直角的平行四边形叫做矩形
概念
一般性质
特有性质
课堂小结
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
