苏科版数学八年级下册9.5 三角形的中位线 同步课件(共13张PPT)
文档属性
| 名称 | 苏科版数学八年级下册9.5 三角形的中位线 同步课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 526.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 07:00:04 | ||
图片预览

文档简介
(共13张PPT)
第九章 中心对称图形——平行四边形
9.5 三角形的中位线
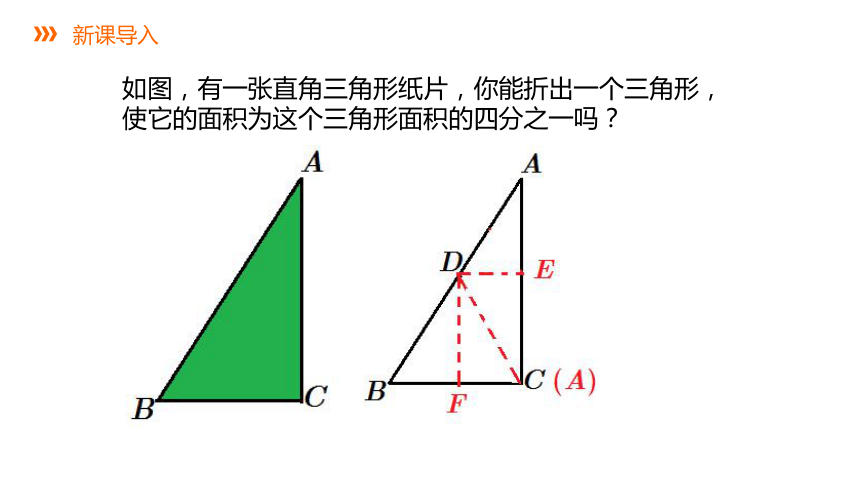
如图,有一张直角三角形纸片,你能折出一个三角形,使它的面积为这个三角形面积的四分之一吗?
新课导入
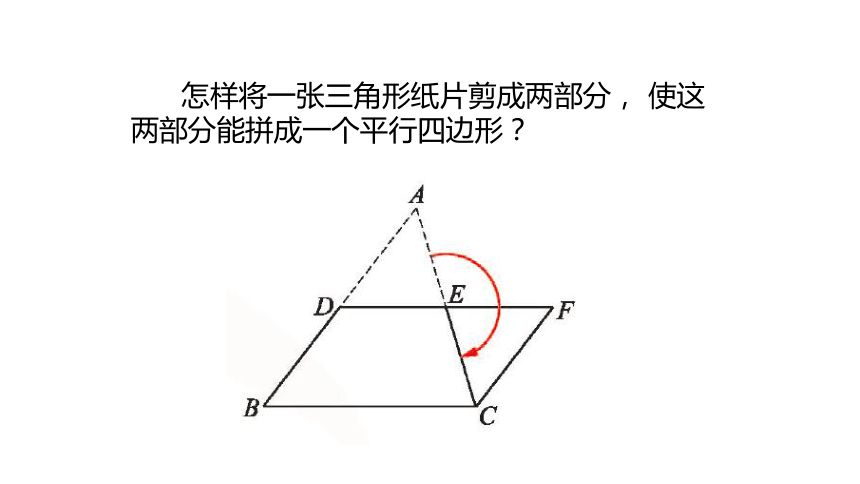
怎样将一张三角形纸片剪成两部分, 使这两部分能拼成一个平行四边形?
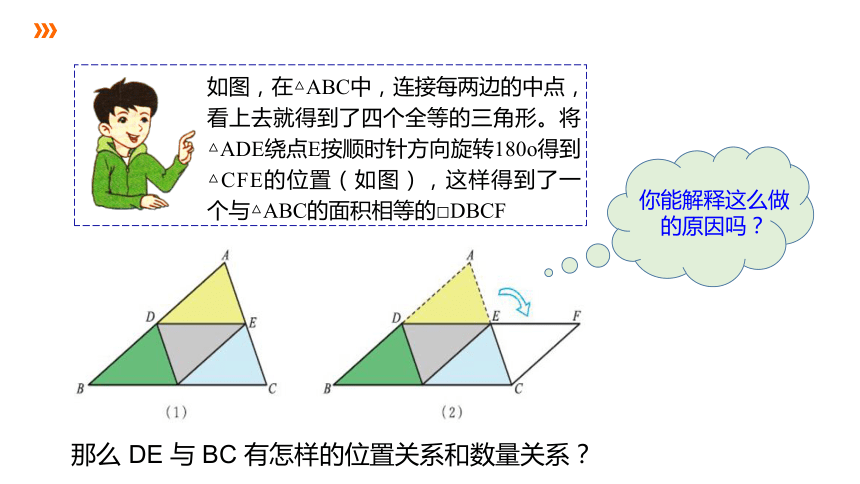
如图,在△ABC中,连接每两边的中点,看上去就得到了四个全等的三角形。将△ADE绕点E按顺时针方向旋转180o得到△CFE的位置(如图),这样得到了一个与△ABC的面积相等的□DBCF
你能解释这么做
的原因吗?
那么 DE 与 BC 有怎样的位置关系和数量关系?
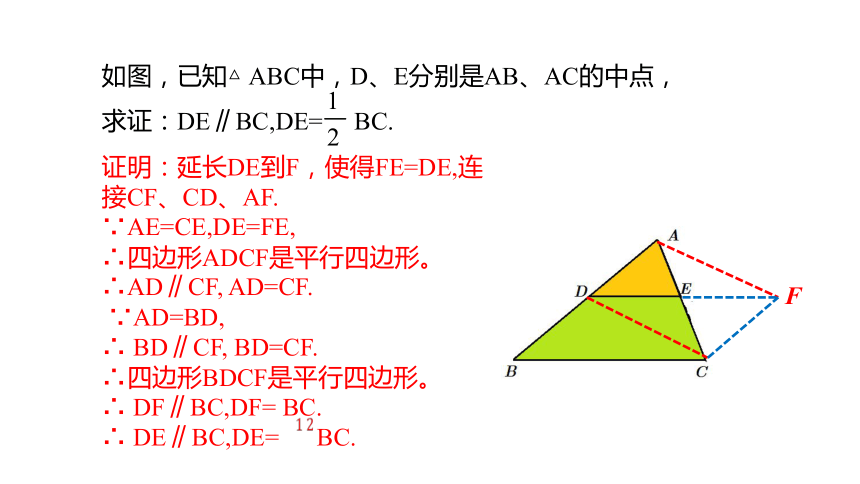
如图,已知△ ABC中,D、E分别是AB、AC的中点,求证:DE∥BC,DE= BC.
F
证明:延长DE到F,使得FE=DE,连接CF、CD、AF.
∵AE=CE,DE=FE,
∴四边形ADCF是平行四边形。
∴AD∥CF, AD=CF.
∵AD=BD,
∴ BD∥CF, BD=CF.
∴四边形BDCF是平行四边形。
∴ DF∥BC,DF= BC.
∴ DE∥BC,DE= BC.
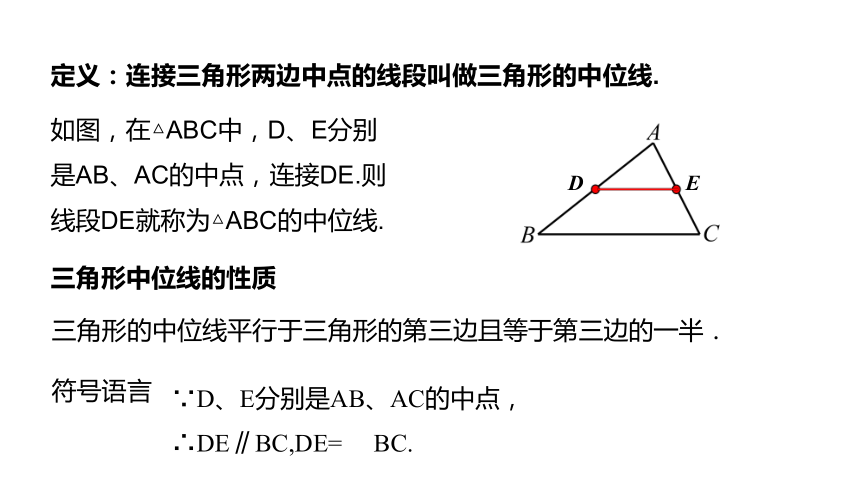
定义:连接三角形两边中点的线段叫做三角形的中位线.
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE.则线段DE就称为△ABC的中位线.
D
E
三角形中位线的性质
三角形的中位线平行于三角形的第三边且等于第三边的一半.
∵D、E分别是AB、AC的中点,
∴DE∥BC,DE= BC.
符号语言
例 如图,四边形ABCD中,AC=BD,点E、F、G、H分别是AB、BC、CD、AD的中点,
求证:四边形EFGH是菱形.
证明:在△ BAC中,
∵BE=EA , BF=FC,
∴EF= 1 2 .(三角形的中位线等于第三边的一半)
同理: FG= 1 2 , GH= 1 2 , HE= 1 2
∵AC=BD
∴EF =FG=GH=HE,
∴四边形EFGH是菱形.(四条边相等的四边形是菱形)
B
720
3.如图,点 D、E、F 分别是 △ABC 的三边AB、BC、 AC的中点:
(1)若∠ADF=50°,则∠B= °;
(2)已知三边AB、BC、AC分别为12、10、8,
则△ DEF的周长为 .
50
15
A
B
C
D
F
E
4. 如图,顺次连接四边形ABCD四边的中点E,F,G,H,则四边形EFGH的形状一定是 .
平行四边形
5.如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
课堂小结
三角形的中位线
三角形中位线平行于第三边,并且等于它的一半
三角形的中位线定理
三角形的中位线定理的应用
第九章 中心对称图形——平行四边形
9.5 三角形的中位线
如图,有一张直角三角形纸片,你能折出一个三角形,使它的面积为这个三角形面积的四分之一吗?
新课导入
怎样将一张三角形纸片剪成两部分, 使这两部分能拼成一个平行四边形?
如图,在△ABC中,连接每两边的中点,看上去就得到了四个全等的三角形。将△ADE绕点E按顺时针方向旋转180o得到△CFE的位置(如图),这样得到了一个与△ABC的面积相等的□DBCF
你能解释这么做
的原因吗?
那么 DE 与 BC 有怎样的位置关系和数量关系?
如图,已知△ ABC中,D、E分别是AB、AC的中点,求证:DE∥BC,DE= BC.
F
证明:延长DE到F,使得FE=DE,连接CF、CD、AF.
∵AE=CE,DE=FE,
∴四边形ADCF是平行四边形。
∴AD∥CF, AD=CF.
∵AD=BD,
∴ BD∥CF, BD=CF.
∴四边形BDCF是平行四边形。
∴ DF∥BC,DF= BC.
∴ DE∥BC,DE= BC.
定义:连接三角形两边中点的线段叫做三角形的中位线.
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE.则线段DE就称为△ABC的中位线.
D
E
三角形中位线的性质
三角形的中位线平行于三角形的第三边且等于第三边的一半.
∵D、E分别是AB、AC的中点,
∴DE∥BC,DE= BC.
符号语言
例 如图,四边形ABCD中,AC=BD,点E、F、G、H分别是AB、BC、CD、AD的中点,
求证:四边形EFGH是菱形.
证明:在△ BAC中,
∵BE=EA , BF=FC,
∴EF= 1 2 .(三角形的中位线等于第三边的一半)
同理: FG= 1 2 , GH= 1 2 , HE= 1 2
∵AC=BD
∴EF =FG=GH=HE,
∴四边形EFGH是菱形.(四条边相等的四边形是菱形)
B
720
3.如图,点 D、E、F 分别是 △ABC 的三边AB、BC、 AC的中点:
(1)若∠ADF=50°,则∠B= °;
(2)已知三边AB、BC、AC分别为12、10、8,
则△ DEF的周长为 .
50
15
A
B
C
D
F
E
4. 如图,顺次连接四边形ABCD四边的中点E,F,G,H,则四边形EFGH的形状一定是 .
平行四边形
5.如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
课堂小结
三角形的中位线
三角形中位线平行于第三边,并且等于它的一半
三角形的中位线定理
三角形的中位线定理的应用
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
