苏科版数学八年级下册12.2 第1课时 二次根式的乘法(1)同步课件(共14张PPT)
文档属性
| 名称 | 苏科版数学八年级下册12.2 第1课时 二次根式的乘法(1)同步课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 274.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 07:13:08 | ||
图片预览



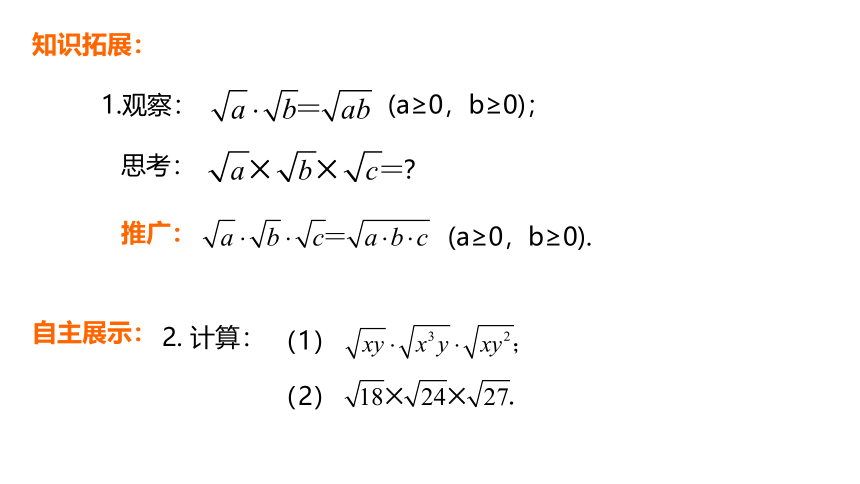
文档简介
(共14张PPT)
第12章 二次根式
12.2 第1课时 二次根式的乘法(1)
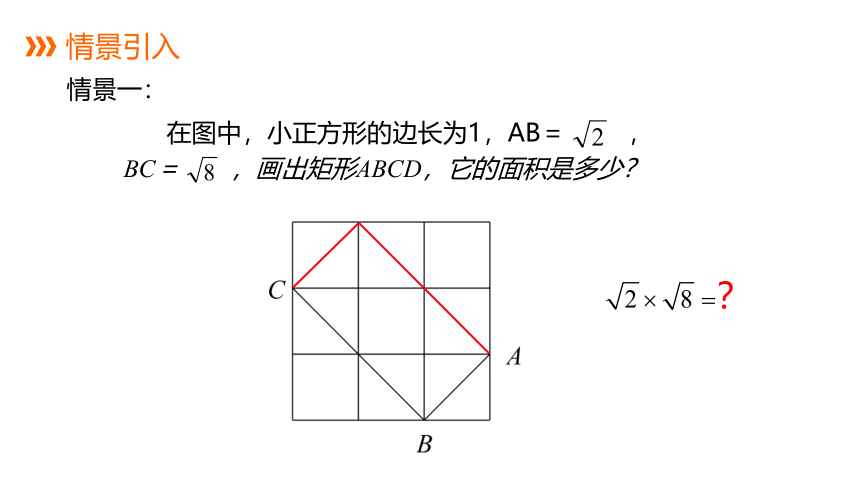
BC= ,画出矩形ABCD,它的面积是多少?
在图中,小正方形的边长为1,AB= ,
情景一:
情景引入
?
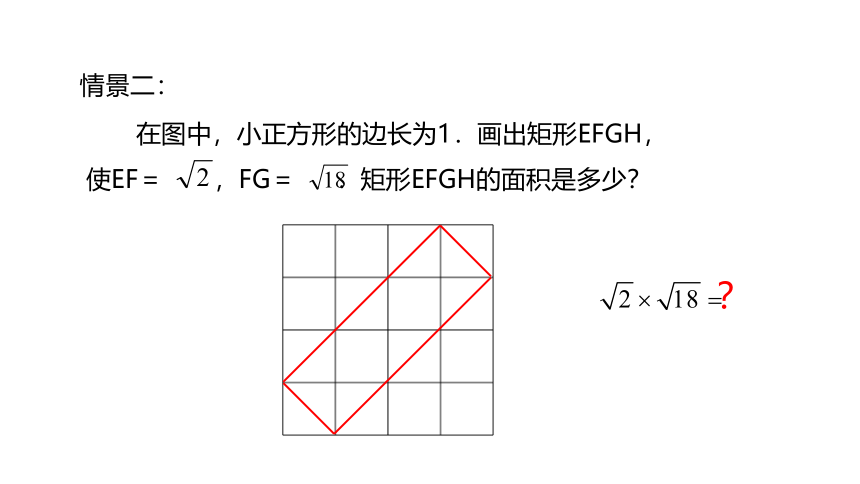
情景二:
在图中,小正方形的边长为1.画出矩形EFGH,使EF= ,FG= .矩形EFGH的面积是多少?
?
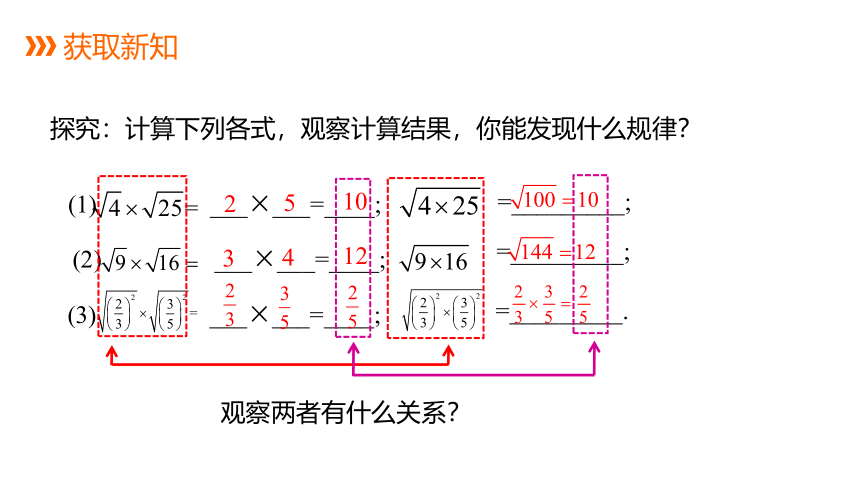
探究:计算下列各式,观察计算结果,你能发现什么规律?
(1) ___×___=____;
=_________;
(2) ___×___=____;
(3) ___×___=____;
=_________;
=_________.
2
5
10
3
4
12
观察两者有什么关系?
获取新知
由此,得:
算术平方根的积等于各个被开方数的积的算术平方根.
文字语言叙述:
二次根式乘法法则: (a≥0,b≥0).
一般地,当a≥0,b≥0时,
由此可知, 都是ab的算术平方根.
利用这个式子,可以进行二次根式的乘法运算.
逆用二次根式乘法法则:
文字语言叙述:
积的算术平方根,等于积中各因式的算术平方根的积.
(a≥0,b≥0).
利用这个式子,可以化简二次根式.
观察: (a≥0,b≥0);
思考:
?
推广:
自主展示:
2. 计算:
(1)
(2)
(a≥0,b≥0).
知识拓展:
例1 计算:
(2)
(1)
(3)
解:(1)
(2)
(3)当a≥0时,
例2 化简:
(1)
(2) (a≥0);
(3) (a≥0, b≥0).
解:
(1)
(2)
(3)
3.如果因式中有平方式(或平方数),应用关系式 =|a|
把这个因式(或因数)开出来,将二次根式化简 .
1.把被开方数分解因式(或因数) ;
2.把各因式(或因数)积的算术平方根化为每个因
式(或因数)的算术平方根的积;
化简二次根式的步骤:
归纳小结
1. 计算:
2. 计算:
(1) ;(2)
解:(1)
(2)
3. 化简:(1) (2) (3)
解:(1)
(2)
(3)
(2)中4a3b2含有像4,a2,b2,这样开的尽方的因数或因式,需把它们开方后移到根号外.
课堂小结
二次根式的乘法
法则
性质
第12章 二次根式
12.2 第1课时 二次根式的乘法(1)
BC= ,画出矩形ABCD,它的面积是多少?
在图中,小正方形的边长为1,AB= ,
情景一:
情景引入
?
情景二:
在图中,小正方形的边长为1.画出矩形EFGH,使EF= ,FG= .矩形EFGH的面积是多少?
?
探究:计算下列各式,观察计算结果,你能发现什么规律?
(1) ___×___=____;
=_________;
(2) ___×___=____;
(3) ___×___=____;
=_________;
=_________.
2
5
10
3
4
12
观察两者有什么关系?
获取新知
由此,得:
算术平方根的积等于各个被开方数的积的算术平方根.
文字语言叙述:
二次根式乘法法则: (a≥0,b≥0).
一般地,当a≥0,b≥0时,
由此可知, 都是ab的算术平方根.
利用这个式子,可以进行二次根式的乘法运算.
逆用二次根式乘法法则:
文字语言叙述:
积的算术平方根,等于积中各因式的算术平方根的积.
(a≥0,b≥0).
利用这个式子,可以化简二次根式.
观察: (a≥0,b≥0);
思考:
?
推广:
自主展示:
2. 计算:
(1)
(2)
(a≥0,b≥0).
知识拓展:
例1 计算:
(2)
(1)
(3)
解:(1)
(2)
(3)当a≥0时,
例2 化简:
(1)
(2) (a≥0);
(3) (a≥0, b≥0).
解:
(1)
(2)
(3)
3.如果因式中有平方式(或平方数),应用关系式 =|a|
把这个因式(或因数)开出来,将二次根式化简 .
1.把被开方数分解因式(或因数) ;
2.把各因式(或因数)积的算术平方根化为每个因
式(或因数)的算术平方根的积;
化简二次根式的步骤:
归纳小结
1. 计算:
2. 计算:
(1) ;(2)
解:(1)
(2)
3. 化简:(1) (2) (3)
解:(1)
(2)
(3)
(2)中4a3b2含有像4,a2,b2,这样开的尽方的因数或因式,需把它们开方后移到根号外.
课堂小结
二次根式的乘法
法则
性质
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
