青岛版九年级数学上册1.2(3)利用两边及夹角判定相似 课件(共24张PPT)
文档属性
| 名称 | 青岛版九年级数学上册1.2(3)利用两边及夹角判定相似 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 761.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 06:15:37 | ||
图片预览





文档简介
(共24张PPT)
1.2 怎样判定三角形相似
第3课时 利用两边及其夹角
判定三角形相似
学习目标
1、了解相似三角形的判定方法二的推导过程。
2、 熟练应用判定方法二去判定三角形相似。
重点:应用判定方法二证明三角形的相似。
难点:能在复杂的图形中,找出证明两个三角形相似的条件;
1.什么是相似三角形?
如果一个三角形的各个角与另一个三角形的各个角对应相等,各边对应成比例,那么这两个三角形叫做相似三角形.
2.我们已经学了哪些相似三角形的判定方法
1、定义法: 2、判定定理1
复习导入
3.相似三角形的性质
1、对应角相等 2、对应边成比例
还有其它
判定方法吗?
探究一:如果两个三角形有两条边成比例,它们一定相似吗?
有两条边成比例,
但不相似.
B
C
A
2
3
B′
C′
A′
4
6
只有两条边成比例的两个三角形,不一定相似.
新课探究
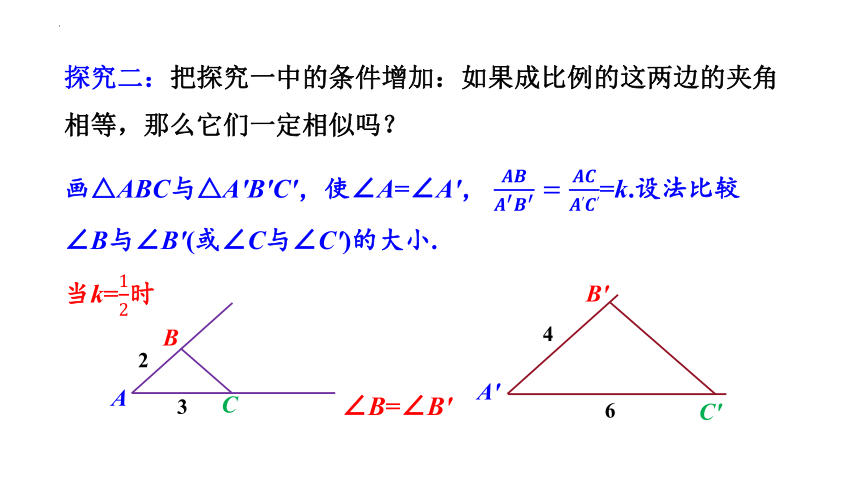
探究二:把探究一中的条件增加:如果成比例的这两边的夹角相等,那么它们一定相似吗?
画△ABC与△A′B′C′,使∠A=∠A′, =k.设法比较∠B与∠B′(或∠C与∠C′)的大小.
当k=时
B
C
A
B′
C′
A′
4
6
2
3
∠B=∠B′
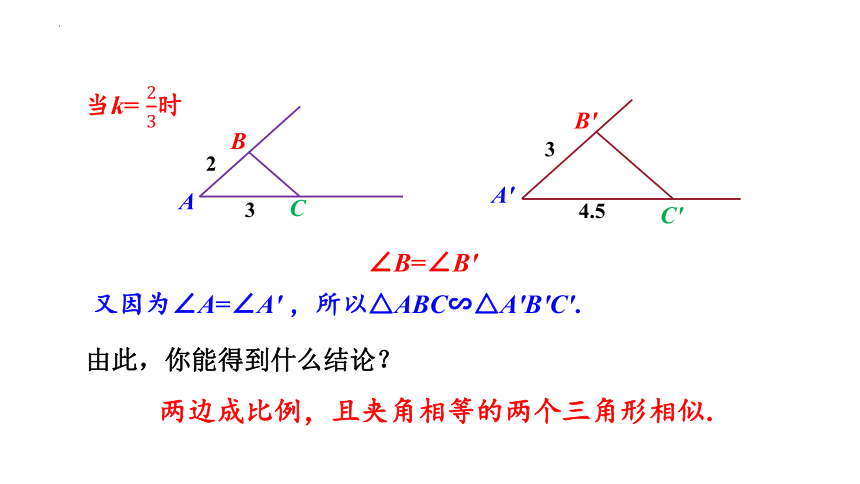
当k= 时
B
C
A
B′
C′
A′
3
4.5
2
3
∠B=∠B′
又因为∠A=∠A′ ,所以△ABC∽△A′B′C′.
由此,你能得到什么结论?
两边成比例,且夹角相等的两个三角形相似.
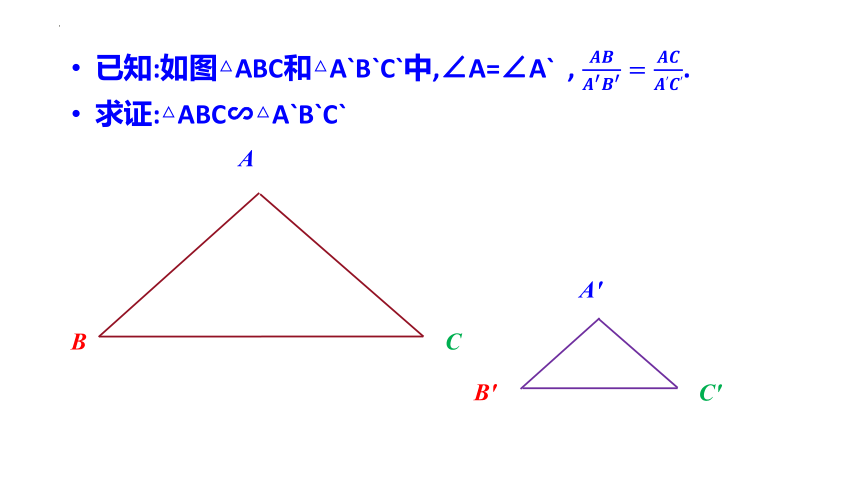
已知:如图△ABC和△A`B`C`中,∠A=∠A` , .
求证:△ABC∽△A`B`C`
B′
C′
A′
B
C
A
已知:如图△ABC和△A`B`C`中,∠A∠A` ,A`B`:AB=A`C`:AC.
求证:△ABC∽△A`B`C`
证明:在AB(或它的延长线)上截取AD=A′B′,过点D作DE∥BC,交AC于点E.于是
∠ADE=∠B且= (基本事实9的推论). ①
∵ =, ②
AD=A′B′,比较①②两式左边和右边,
∴ = . ∴ AE=A′C′.
∵∠A′=∠A,∴ △ADE≌△A′B′C′ (SAS).
B
C
A
B′
C′
A′
D
E
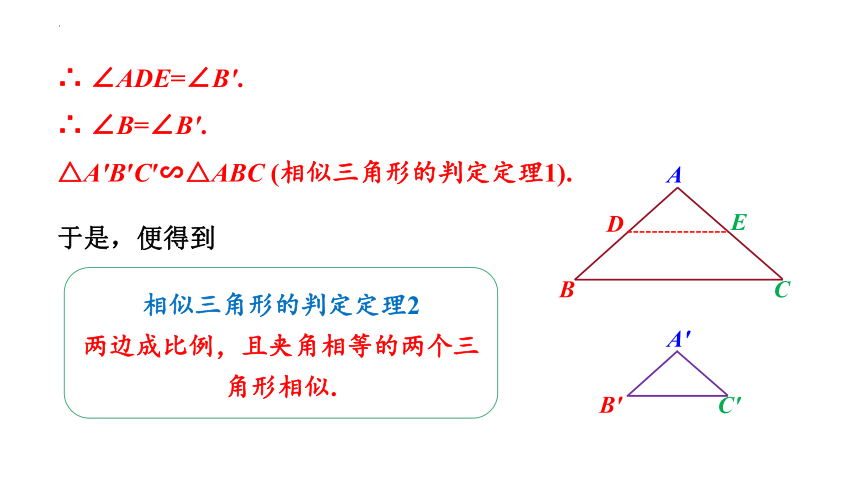
∴ ∠ADE=∠B′.
∴ ∠B=∠B′.
△A′B′C′∽△ABC (相似三角形的判定定理1).
B
C
A
B′
C′
A′
D
E
相似三角形的判定定理2
两边成比例,且夹角相等的两个三角形相似.
于是,便得到
定理:两边成比例,且夹角相等的两个三角形相似.
你能用符号语言表示这个定理吗?
A′
B ′
C ′
C
A
B
定理:两边成比例,且夹角相等的两个三角形相似.
你能用符号语言表示这个定理吗?
在△ABC与△A′B′C′中,
∵ ,∠A=∠A′,
∴ △ABC∽△A′B′C′ .
夹角
A′
B ′
C ′
C
A
B
【例1】如图,AD=3,AE=4,BE=5,CD=9 ,△ADE与△ABC相似吗?说明理由
【例1】如图,AD=3,AE=4,BE=5,CD=9 ,△ADE与△ABC相似吗?说明理由
解:△ADE∽△ABC
∵ =,
∴
又∵∠EAD=∠CAB,
∴△ADE∽△ABC.
【跟踪练习1】如图所示,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 = ,求DE的长.
B
C
A
D
E
【跟踪练习1】如图所示,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 = ,求DE的长.
B
C
A
D
E
解: ∵ AE=1.5,AC=2,
∴ =.
∵ =,
又∵∠EAD=∠CAB
∴△ADE∽△ABC.
∴ = =.
∴ = .
∵BC=3,
∴DE= BC= .
【例2】在△ABC中,∠C=90°,D,E分别为AB,AC上的点,且 AD·AB= AE·AC,求证AB⊥ED
证明:∵AD·AB=AE·AC
∴∠ADE=∠C=90°
∴AB⊥ED
【跟踪练习2】已知:如图BE与CD相交于点O,AD·AB=AE·AC。
求证:△BOD∽△COE
A
B
C
D
E
O
证明:∵AD·AB=AE·AC
∴∠B=∠C
∵∠BOD=∠COE
∴△BOD∽△COE
1、如图,ABCD,CDEF,EFGH是三个相连的正方形,连接
AC,AF,AG.你能证明△ACF∽△GCA吗?试一试。
B
A
C
D
F
E
G
H
解:设各正方形的边长为a,
∴AB=BC=CF=a,BF=CG=2a,
由勾股定理,得
三、合作交流
目前,我们知道了哪些判定两个三角形相似的方法?
方法一:根据相似三角形的定义进行判定.
方法二:根据定理“两角分别相等的两个三角形相似”进行判定.
方法三:根据定理“两边成比例且夹角相等的两个三角形相似”进行判定.
方法总结
1.如图,AB⊥BC,CD⊥BC,点E在BC上且AE⊥DE,若AB=1.5,BE=3 ,CE=3.5,求CD的长
达标检测
2.如图,AB=6,AC=4,AD=3,AE=2 ,DE=2.5,求BC的长
3.如图,在 △ABC 中,CD是AB边上的高,且 . 求证:∠ACB=90°.
A
B
C
D
CD2=AD·BD
证明:∵ CD是边AB上的高,
∴ ∠ADC= ∠CDB=90°.
∵ CD2=AD·BD
∴ = ,
∴ △ ADC∽△CDB.
∴ ∠ACD= ∠B.
∴ ∠ACB= ∠ACD+ ∠BCD= ∠B+ ∠BCD= 90°.
3.如图,在 △ABC 中,CD是AB边上的高,且 . 求证:∠ACB=90°.
A
B
C
D
CD2=AD·BD
4. △ABC为锐角三角形,BD、CE分别为AC、AB边上的高 .
求证:△ ADE∽ △ ABC.
证明:∵ BD⊥AC,CE⊥AB,
∴ ∠AEC=∠ADB= 90°
∴ ∠ABD+∠A=90°, ∠ACE+∠A= 90°.
∴ ∠ABD= ∠ACE.
又∵ ∠A= ∠A,
∴ △ ABD ∽△ ACE.
∴
∵ ∠A= ∠A,
∴ △ ADE ∽ △ ABC.
1.2 怎样判定三角形相似
第3课时 利用两边及其夹角
判定三角形相似
学习目标
1、了解相似三角形的判定方法二的推导过程。
2、 熟练应用判定方法二去判定三角形相似。
重点:应用判定方法二证明三角形的相似。
难点:能在复杂的图形中,找出证明两个三角形相似的条件;
1.什么是相似三角形?
如果一个三角形的各个角与另一个三角形的各个角对应相等,各边对应成比例,那么这两个三角形叫做相似三角形.
2.我们已经学了哪些相似三角形的判定方法
1、定义法: 2、判定定理1
复习导入
3.相似三角形的性质
1、对应角相等 2、对应边成比例
还有其它
判定方法吗?
探究一:如果两个三角形有两条边成比例,它们一定相似吗?
有两条边成比例,
但不相似.
B
C
A
2
3
B′
C′
A′
4
6
只有两条边成比例的两个三角形,不一定相似.
新课探究
探究二:把探究一中的条件增加:如果成比例的这两边的夹角相等,那么它们一定相似吗?
画△ABC与△A′B′C′,使∠A=∠A′, =k.设法比较∠B与∠B′(或∠C与∠C′)的大小.
当k=时
B
C
A
B′
C′
A′
4
6
2
3
∠B=∠B′
当k= 时
B
C
A
B′
C′
A′
3
4.5
2
3
∠B=∠B′
又因为∠A=∠A′ ,所以△ABC∽△A′B′C′.
由此,你能得到什么结论?
两边成比例,且夹角相等的两个三角形相似.
已知:如图△ABC和△A`B`C`中,∠A=∠A` , .
求证:△ABC∽△A`B`C`
B′
C′
A′
B
C
A
已知:如图△ABC和△A`B`C`中,∠A∠A` ,A`B`:AB=A`C`:AC.
求证:△ABC∽△A`B`C`
证明:在AB(或它的延长线)上截取AD=A′B′,过点D作DE∥BC,交AC于点E.于是
∠ADE=∠B且= (基本事实9的推论). ①
∵ =, ②
AD=A′B′,比较①②两式左边和右边,
∴ = . ∴ AE=A′C′.
∵∠A′=∠A,∴ △ADE≌△A′B′C′ (SAS).
B
C
A
B′
C′
A′
D
E
∴ ∠ADE=∠B′.
∴ ∠B=∠B′.
△A′B′C′∽△ABC (相似三角形的判定定理1).
B
C
A
B′
C′
A′
D
E
相似三角形的判定定理2
两边成比例,且夹角相等的两个三角形相似.
于是,便得到
定理:两边成比例,且夹角相等的两个三角形相似.
你能用符号语言表示这个定理吗?
A′
B ′
C ′
C
A
B
定理:两边成比例,且夹角相等的两个三角形相似.
你能用符号语言表示这个定理吗?
在△ABC与△A′B′C′中,
∵ ,∠A=∠A′,
∴ △ABC∽△A′B′C′ .
夹角
A′
B ′
C ′
C
A
B
【例1】如图,AD=3,AE=4,BE=5,CD=9 ,△ADE与△ABC相似吗?说明理由
【例1】如图,AD=3,AE=4,BE=5,CD=9 ,△ADE与△ABC相似吗?说明理由
解:△ADE∽△ABC
∵ =,
∴
又∵∠EAD=∠CAB,
∴△ADE∽△ABC.
【跟踪练习1】如图所示,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 = ,求DE的长.
B
C
A
D
E
【跟踪练习1】如图所示,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 = ,求DE的长.
B
C
A
D
E
解: ∵ AE=1.5,AC=2,
∴ =.
∵ =,
又∵∠EAD=∠CAB
∴△ADE∽△ABC.
∴ = =.
∴ = .
∵BC=3,
∴DE= BC= .
【例2】在△ABC中,∠C=90°,D,E分别为AB,AC上的点,且 AD·AB= AE·AC,求证AB⊥ED
证明:∵AD·AB=AE·AC
∴∠ADE=∠C=90°
∴AB⊥ED
【跟踪练习2】已知:如图BE与CD相交于点O,AD·AB=AE·AC。
求证:△BOD∽△COE
A
B
C
D
E
O
证明:∵AD·AB=AE·AC
∴∠B=∠C
∵∠BOD=∠COE
∴△BOD∽△COE
1、如图,ABCD,CDEF,EFGH是三个相连的正方形,连接
AC,AF,AG.你能证明△ACF∽△GCA吗?试一试。
B
A
C
D
F
E
G
H
解:设各正方形的边长为a,
∴AB=BC=CF=a,BF=CG=2a,
由勾股定理,得
三、合作交流
目前,我们知道了哪些判定两个三角形相似的方法?
方法一:根据相似三角形的定义进行判定.
方法二:根据定理“两角分别相等的两个三角形相似”进行判定.
方法三:根据定理“两边成比例且夹角相等的两个三角形相似”进行判定.
方法总结
1.如图,AB⊥BC,CD⊥BC,点E在BC上且AE⊥DE,若AB=1.5,BE=3 ,CE=3.5,求CD的长
达标检测
2.如图,AB=6,AC=4,AD=3,AE=2 ,DE=2.5,求BC的长
3.如图,在 △ABC 中,CD是AB边上的高,且 . 求证:∠ACB=90°.
A
B
C
D
CD2=AD·BD
证明:∵ CD是边AB上的高,
∴ ∠ADC= ∠CDB=90°.
∵ CD2=AD·BD
∴ = ,
∴ △ ADC∽△CDB.
∴ ∠ACD= ∠B.
∴ ∠ACB= ∠ACD+ ∠BCD= ∠B+ ∠BCD= 90°.
3.如图,在 △ABC 中,CD是AB边上的高,且 . 求证:∠ACB=90°.
A
B
C
D
CD2=AD·BD
4. △ABC为锐角三角形,BD、CE分别为AC、AB边上的高 .
求证:△ ADE∽ △ ABC.
证明:∵ BD⊥AC,CE⊥AB,
∴ ∠AEC=∠ADB= 90°
∴ ∠ABD+∠A=90°, ∠ACE+∠A= 90°.
∴ ∠ABD= ∠ACE.
又∵ ∠A= ∠A,
∴ △ ABD ∽△ ACE.
∴
∵ ∠A= ∠A,
∴ △ ADE ∽ △ ABC.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
