沪科版数学八年级下册 18.1勾股定理课件(共14张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 18.1勾股定理课件(共14张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 465.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 00:00:00 | ||
图片预览




文档简介
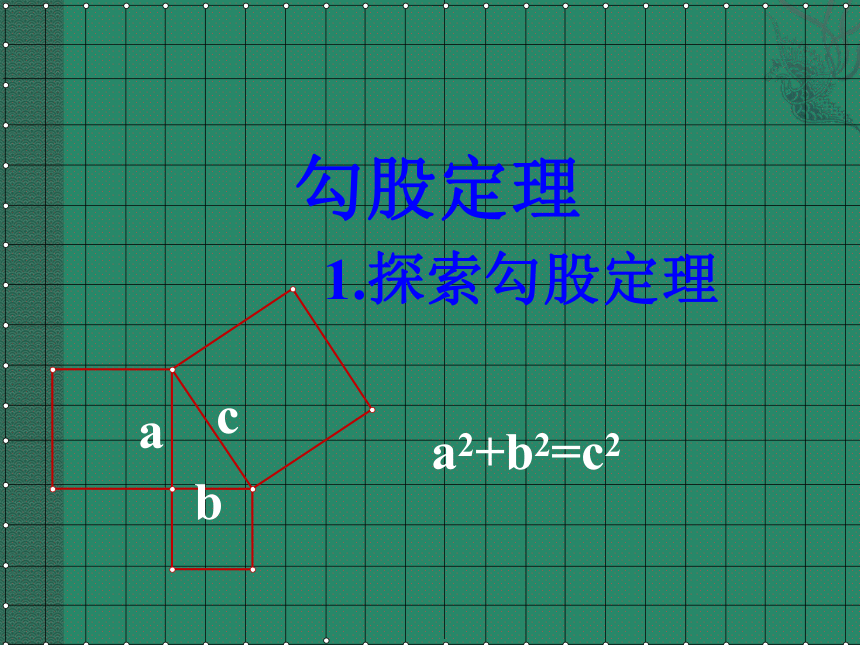
(共14张PPT)
b
a
c
a2+b2=c2
勾股定理 1.探索勾股定理
A
B
C
图1—1
(1)观察图1—1:
正方形A中含有 个小方格,即A的面积是 个单位面积;
正方形B中含有 个小方格,即B的面积是 个单位面积;
正方形C中含有 个小方格,即C的面积是 个单位面积.
9
9
9
9
18
18
A的面积+ B的面积= C的面积
图1—2
A
B
C
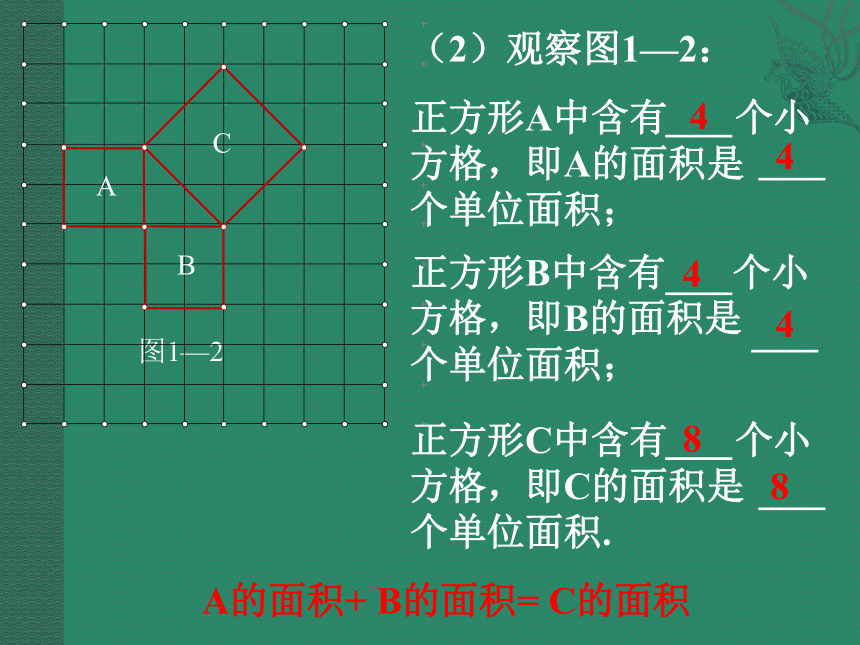
(2)观察图1—2:
正方形A中含有 个小方格,即A的面积是 个单位面积;
正方形B中含有 个小方格,即B的面积是 个单位面积;
正方形C中含有 个小方格,即C的面积是 个单位面积.
4
4
4
4
8
8
A的面积+ B的面积= C的面积
A
B
C
A
B
C
图1—3
图1—4
做一做:
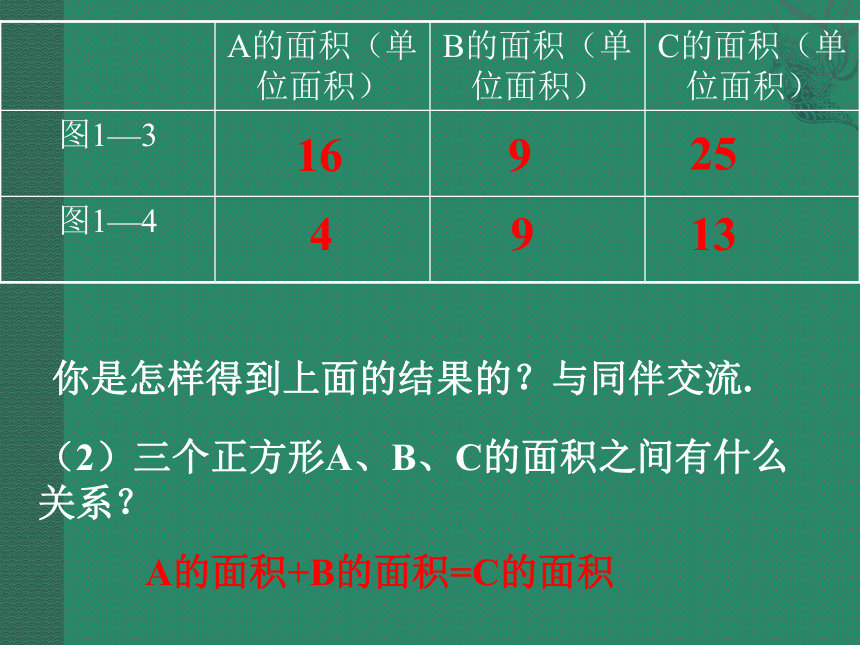
(1)观察图1—3、图1—4,并填写下一页的表格.
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图1—3
图1—4
16
9
25
4
9
13
你是怎样得到上面的结果的?与同伴交流.
(2)三个正方形A、B、C的面积之间有什么关系?
A的面积+B的面积=C的面积
议一议:
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
两直角边的平方和等于斜边的平方
(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量其斜边的长度;(2)中的规律对这个三角形仍然成立吗?
c
a
b
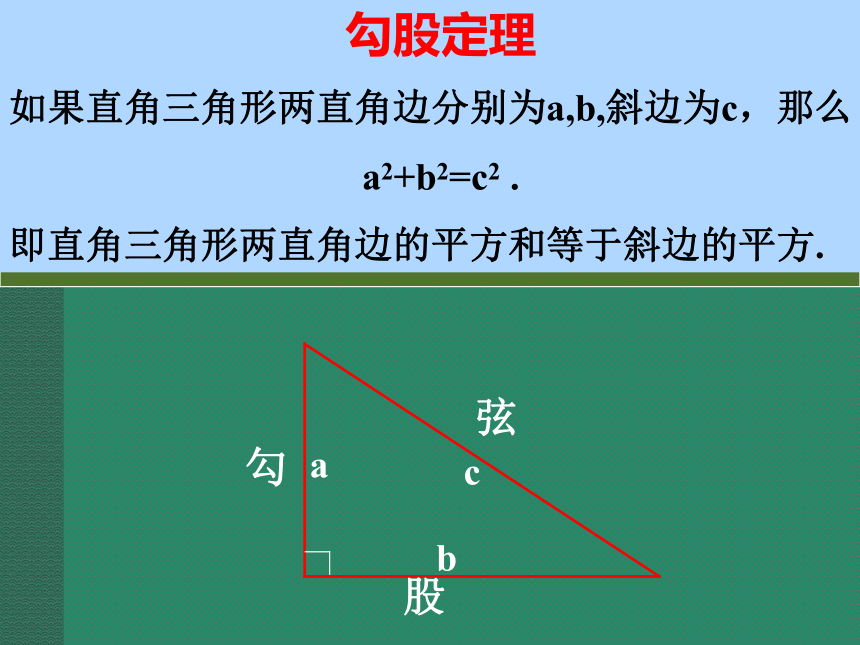
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2+b2=c2 .
即直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
小明妈妈买了一部29英寸(74厘米)的电视机,小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
想一想:
58厘米
46厘米
74厘米
练习:
1.求下列图中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
2.求出下列直角三角形中未知边的长度.
6
8
x
5
x
13
解:由勾股定理,得
=36+64,
即x2 =100.
x2=62+82
∴ x=10.
x2+52=132 .
∴ x2=132-52 ,
即x2 =144 .
∴ x=12.
∵ x > 0,
∵ x > 0 ,
解:由勾股定理,得
3.在直角三角形ABC中, ∠C=900,
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b.
4 .一直角三角形的一直角边长为7, 另两条边长为两个连续整数,求这个直角三角形的周长.
5 .如果一个直角三角形的三条边长是三个连续整数,求这个直角三角形各边的长.
6. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
小结:
1.利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积).
2.探索了直角三角形的三边关系,得到勾股定理:
直角三角形两直角边的平方和等于斜边的平方平方.
C
c
b
a
A
B
A的面积+B的面积=C的面积
a2+b2=c2
读一读
勾股世界
我国是最早了解勾股定理的国家之一.早在三多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名的数学著作《周髀算经》中.在这本书中的另一处,还记载了勾股定理的一般形式.
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前.
相传二千多年前,希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理.为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票,你能看出邮票上的图案所反映的内容吗?
b
a
c
a2+b2=c2
勾股定理 1.探索勾股定理
A
B
C
图1—1
(1)观察图1—1:
正方形A中含有 个小方格,即A的面积是 个单位面积;
正方形B中含有 个小方格,即B的面积是 个单位面积;
正方形C中含有 个小方格,即C的面积是 个单位面积.
9
9
9
9
18
18
A的面积+ B的面积= C的面积
图1—2
A
B
C
(2)观察图1—2:
正方形A中含有 个小方格,即A的面积是 个单位面积;
正方形B中含有 个小方格,即B的面积是 个单位面积;
正方形C中含有 个小方格,即C的面积是 个单位面积.
4
4
4
4
8
8
A的面积+ B的面积= C的面积
A
B
C
A
B
C
图1—3
图1—4
做一做:
(1)观察图1—3、图1—4,并填写下一页的表格.
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图1—3
图1—4
16
9
25
4
9
13
你是怎样得到上面的结果的?与同伴交流.
(2)三个正方形A、B、C的面积之间有什么关系?
A的面积+B的面积=C的面积
议一议:
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
两直角边的平方和等于斜边的平方
(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量其斜边的长度;(2)中的规律对这个三角形仍然成立吗?
c
a
b
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2+b2=c2 .
即直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
小明妈妈买了一部29英寸(74厘米)的电视机,小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
想一想:
58厘米
46厘米
74厘米
练习:
1.求下列图中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
2.求出下列直角三角形中未知边的长度.
6
8
x
5
x
13
解:由勾股定理,得
=36+64,
即x2 =100.
x2=62+82
∴ x=10.
x2+52=132 .
∴ x2=132-52 ,
即x2 =144 .
∴ x=12.
∵ x > 0,
∵ x > 0 ,
解:由勾股定理,得
3.在直角三角形ABC中, ∠C=900,
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b.
4 .一直角三角形的一直角边长为7, 另两条边长为两个连续整数,求这个直角三角形的周长.
5 .如果一个直角三角形的三条边长是三个连续整数,求这个直角三角形各边的长.
6. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
小结:
1.利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积).
2.探索了直角三角形的三边关系,得到勾股定理:
直角三角形两直角边的平方和等于斜边的平方平方.
C
c
b
a
A
B
A的面积+B的面积=C的面积
a2+b2=c2
读一读
勾股世界
我国是最早了解勾股定理的国家之一.早在三多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名的数学著作《周髀算经》中.在这本书中的另一处,还记载了勾股定理的一般形式.
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前.
相传二千多年前,希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理.为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票,你能看出邮票上的图案所反映的内容吗?
