北京版九年级数学上册第20章 复习解直角三角形----几何应用教学设计(表格式)
文档属性
| 名称 | 北京版九年级数学上册第20章 复习解直角三角形----几何应用教学设计(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 108.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 00:00:00 | ||
图片预览

文档简介
课题 第20章 复习 解直角三角形----几何应用 总课时 3 第3课时 授课人
教学 目标 掌握非直角三角形中的锐角三角函数和线段长的求解问题. 经历画图和添辅助线的思考和操作过程,完成把非直角三角形的问题转化含目标角直角三角形的问题来解决 培养画图能力、提高计算能力。渗透转化思想和方程思想。 鼓励大胆创新、尝试多途径解决问题的精神。获得成功的体验。
教学重点 非直角三角形的锐角三角函数和线段长的求解问题.
教学难点 画图、准确添加辅助线
教学方法 分析------启发 传递-----接受
教学准备 多媒体
教 学 过 程 教 学 过 程 教师活动 学生活动及预设 设计意图
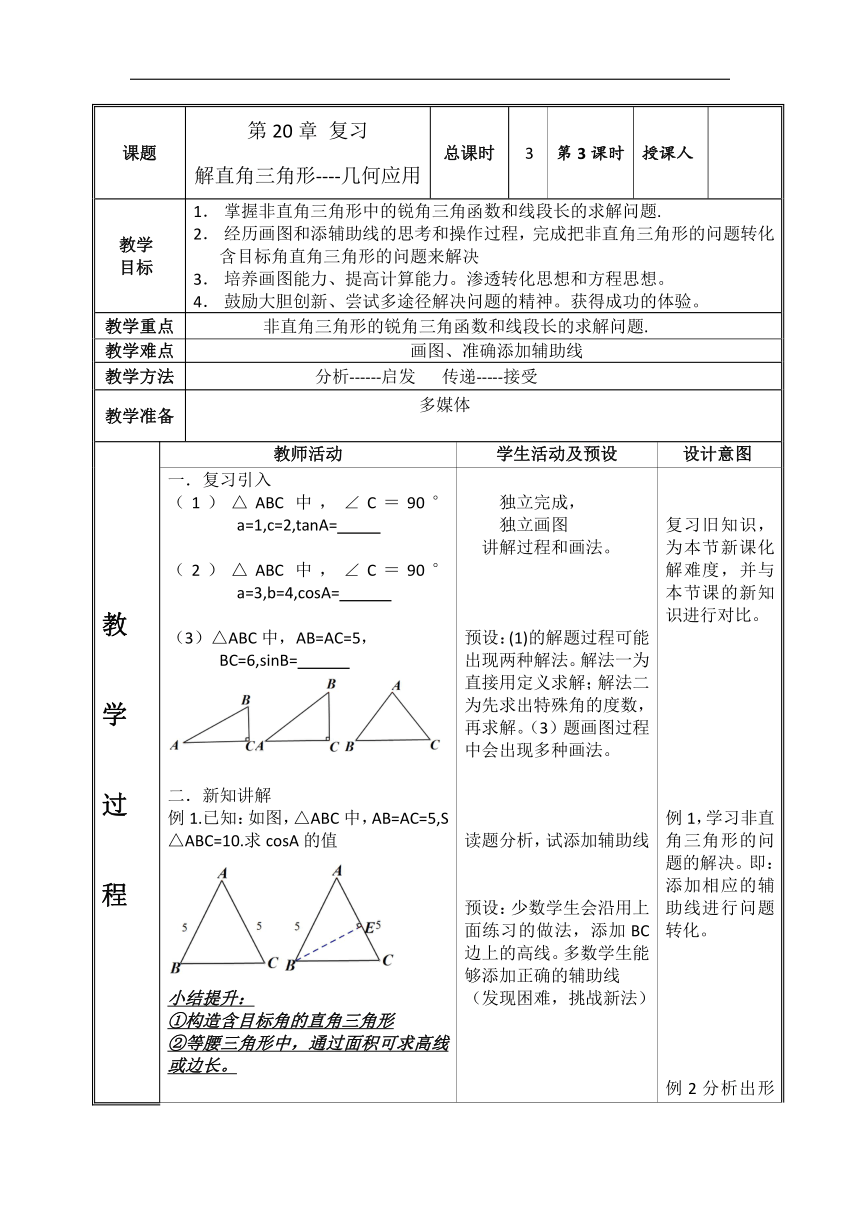
复习引入 (1)△ABC中,∠C=90°a=1,c=2,tanA= (2)△ABC中,∠C=90°a=3,b=4,cosA= (3)△ABC中,AB=AC=5, BC=6,sinB= 二.新知讲解 例1.已知:如图,△ABC中,AB=AC=5,S△ABC=10.求cosA的值 小结提升: ①构造含目标角的直角三角形 ②等腰三角形中,通过面积可求高线或边长。 例2.已知:∠A=120,AC=2,BC=2 求(1)tanB (2) AB的长 小结提升: ③保留特殊角 练习巩固 1.已知,△ABC中,∠B=60°, ∠BAC=75°,AB=4,BC= 2.如图,在△ABC中,∠A=135° ∠C=30°,BC=6,AB的长为 3.练习.已知:∠A=30°,AC=2,BC= 则∠ABC的度数为 四.小结提升 ①构造目标角所在直角三角形 ②等腰三角形中,通过面积可求高线或边长。 ③保留特殊角 独立完成, 独立画图 讲解过程和画法。 预设:(1)的解题过程可能出现两种解法。解法一为直接用定义求解;解法二为先求出特殊角的度数,再求解。(3)题画图过程中会出现多种画法。 读题分析,试添加辅助线 预设:少数学生会沿用上面练习的做法,添加BC边上的高线。多数学生能够添加正确的辅助线 (发现困难,挑战新法) 读题,思考,独立画图。展示画图并试分析 总结特殊角 预设:①画图困难。②有的学生会添加内高,从而发现此法碰壁,另求新法。 - 读题,分析,试做 预设:1.会较为顺利 2.会有少数学生没有思路 3.多数人会忽略分类思想 在时间充裕的情况下,学生独立完成、独立分析,分组交流。 归纳本节课各环节的小结 复习旧知识,为本节新课化解难度,并与本节课的新知识进行对比。 例1,学习非直角三角形的问题的解决。即:添加相应的辅助线进行问题转化。 例2分析出形内作高不能得出结论,从而要考虑形外高 对本节课知识进行巩固和提升,渗透分类讨论思想。 总结提升
教学 目标 掌握非直角三角形中的锐角三角函数和线段长的求解问题. 经历画图和添辅助线的思考和操作过程,完成把非直角三角形的问题转化含目标角直角三角形的问题来解决 培养画图能力、提高计算能力。渗透转化思想和方程思想。 鼓励大胆创新、尝试多途径解决问题的精神。获得成功的体验。
教学重点 非直角三角形的锐角三角函数和线段长的求解问题.
教学难点 画图、准确添加辅助线
教学方法 分析------启发 传递-----接受
教学准备 多媒体
教 学 过 程 教 学 过 程 教师活动 学生活动及预设 设计意图
复习引入 (1)△ABC中,∠C=90°a=1,c=2,tanA= (2)△ABC中,∠C=90°a=3,b=4,cosA= (3)△ABC中,AB=AC=5, BC=6,sinB= 二.新知讲解 例1.已知:如图,△ABC中,AB=AC=5,S△ABC=10.求cosA的值 小结提升: ①构造含目标角的直角三角形 ②等腰三角形中,通过面积可求高线或边长。 例2.已知:∠A=120,AC=2,BC=2 求(1)tanB (2) AB的长 小结提升: ③保留特殊角 练习巩固 1.已知,△ABC中,∠B=60°, ∠BAC=75°,AB=4,BC= 2.如图,在△ABC中,∠A=135° ∠C=30°,BC=6,AB的长为 3.练习.已知:∠A=30°,AC=2,BC= 则∠ABC的度数为 四.小结提升 ①构造目标角所在直角三角形 ②等腰三角形中,通过面积可求高线或边长。 ③保留特殊角 独立完成, 独立画图 讲解过程和画法。 预设:(1)的解题过程可能出现两种解法。解法一为直接用定义求解;解法二为先求出特殊角的度数,再求解。(3)题画图过程中会出现多种画法。 读题分析,试添加辅助线 预设:少数学生会沿用上面练习的做法,添加BC边上的高线。多数学生能够添加正确的辅助线 (发现困难,挑战新法) 读题,思考,独立画图。展示画图并试分析 总结特殊角 预设:①画图困难。②有的学生会添加内高,从而发现此法碰壁,另求新法。 - 读题,分析,试做 预设:1.会较为顺利 2.会有少数学生没有思路 3.多数人会忽略分类思想 在时间充裕的情况下,学生独立完成、独立分析,分组交流。 归纳本节课各环节的小结 复习旧知识,为本节新课化解难度,并与本节课的新知识进行对比。 例1,学习非直角三角形的问题的解决。即:添加相应的辅助线进行问题转化。 例2分析出形内作高不能得出结论,从而要考虑形外高 对本节课知识进行巩固和提升,渗透分类讨论思想。 总结提升
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
