22.1.2 二次函数y=ax2的图象和性质 教案
文档属性
| 名称 | 22.1.2 二次函数y=ax2的图象和性质 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 07:56:35 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
22.1.2 二次函数y=ax2的图象和性质 教案
课题 22.1.2 二次函数y=ax2的图象和性质 单元 第22单元 学科 数学 年级 九年级(上)
学习目标 1.能够用描点法画函数的图象,并能根据图象认识和理解其性质.2.初步建立二次函数表达式与图象之间的联系,体会数与形结合与转化.
重点 1.理解并掌握二次函数y=ax2的性质.2.掌握二次项系数a的作用.
难点 理解并掌握二次函数y=ax2的性质.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题 复习回顾:1.画函数图象的方法和步骤?方法:描点法;步骤:列表——描点——连线;列表:注意自变量的取值范围;描点:先建系,根据表格确定点的坐标;连线:用光滑的曲线连接.探究二次函数y = x2的图象和性质用描点法画二次函数 y = x2 的图象解:(1) 列表(2) 描点(3) 连线x...-2-1012...y...41014... y y=x2 o x观察二次函数 y=x2 的图象,回答下面问题:二次函数y=x2 的图象是抛物线;开口向上;轴对称图形,对称轴为y轴抛物线与对称轴的交点叫做顶点,y=x2的顶点为(0,0),顶点是最低点;有最小函数值,当x=0时,y最小=0在对称轴y轴的左侧,y随x的增大而减小;在对称轴y轴的左侧,y随x的增大而增大.以上(2)—(6)是函数y=x2的性质. 思考自议回顾一次函数、正比例函数的图象和性质以及画函数图象的方法及步骤. 通过自学、交流和探究,总结规律.
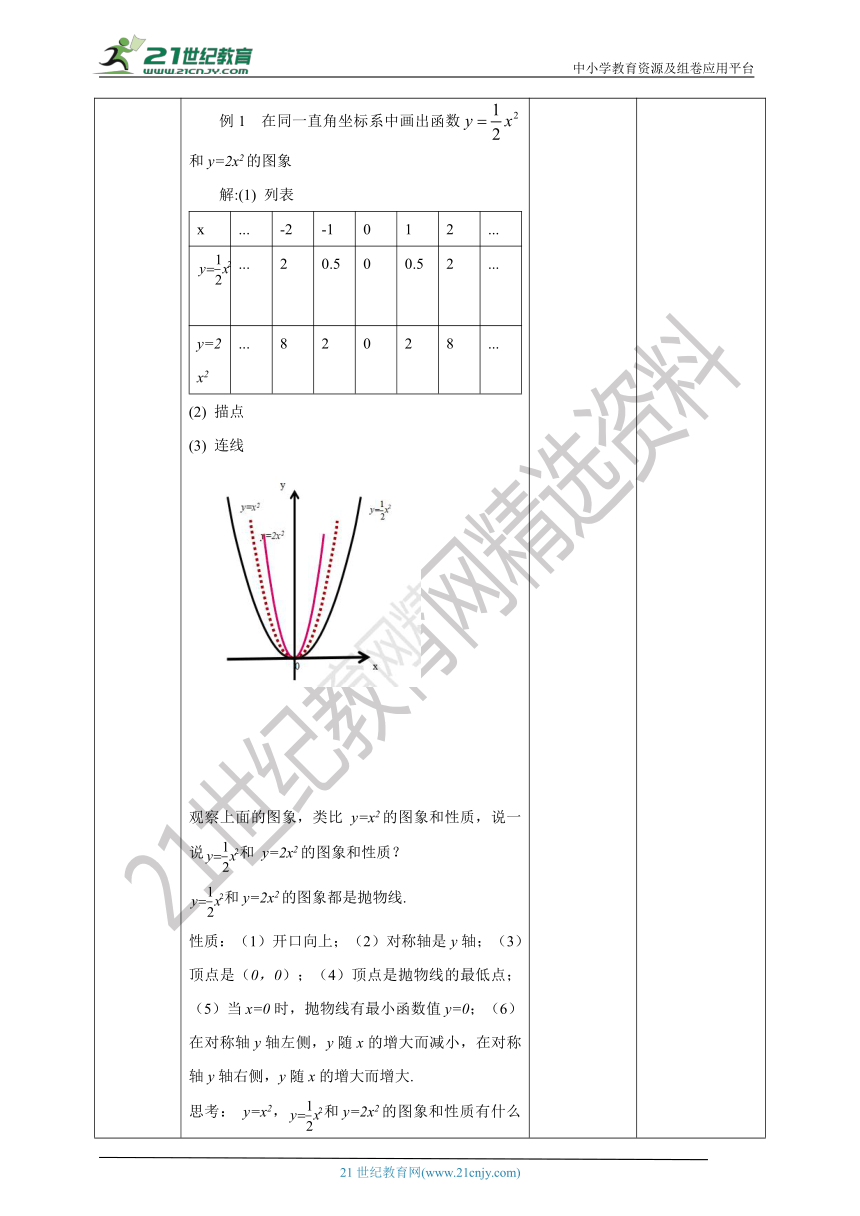
讲授新课 提炼概念 归纳总结:a>0,开口向上,对称轴为y轴;顶点(0、0);函数值有最小值;增减性:在对称轴y轴左侧,y随x的增大而减小,在y轴右侧,y随x的增大而增大.a<0,开口向下,对称轴为y轴;顶点(0、0);函数值有最大值;增减性:在对称轴y轴左侧,y随x的增大而增大,在y轴右侧,y随x的增大而减小.|a|越大,抛物线的开口越小.a>0图象 a<0图象三、典例精讲例1 在同一直角坐标系中画出函数和y=2x2的图象解:(1) 列表x...-2-1012......20.500.52...y=2x2...82028...(2) 描点(3) 连线 观察上面的图象,类比 y=x2的图象和性质,说一说和 y=2x2的图象和性质?和y=2x2的图象都是抛物线. 性质:(1)开口向上;(2)对称轴是y轴;(3)顶点是(0,0);(4)顶点是抛物线的最低点;(5)当x=0时,抛物线有最小函数值y=0;(6)在对称轴y轴左侧,y随x的增大而减小,在对称轴y轴右侧,y随x的增大而增大.思考: y=x2,和y=2x2的图象和性质有什么相同点和不同点 相同点:图象都是抛物线,开口方向、对称轴、顶点、最小值、增减性、对称性都相同;不同点:解析式中的a值不同,图象的开口大小不同.小结:a>0,a越大,抛物线的开口越小.小结:a>0时,二次函数y=ax2的图象和性质:图象都是抛物线,性质:(1)开口方向:开口向上;. (2)开口大小:a越大,抛物线的开口越小; (3)轴对称图形,对称轴为y轴;(4)顶点(0、0); (5)当x=0时二次函数的函数值有最小值为y=0; (6)增减性:在对称轴y轴左侧,y随x的增大而减小,在对称轴y轴右侧,y随x的增大而增大.探究:画出 y= -x2,和 y= -2x2的图象,并说出它们的性质. 图象都是抛物线,性质:(1)开口向下;. (2)对称轴为y轴; (3)顶点(0、0); (4)函数值有最大值; (5)增减性:在对称轴y轴左侧,y随x的增大而增大,在y轴右侧,y随x的增大而减小.不同点:解析式中的a值不同,图象的开口大小不同.小结:a<0,|a|越大,抛物线的开口越小. 体会数形结合的数学思想,结合图形探究性质,为下面探究y = ax2的图象和性质奠定基础. 从具体问题到一般规律获得二次函数y =a x2的性质.
课堂检测 四、巩固训练 1. 关于二次函数y=3x2的图象,下列说法错误的是( )A.它是一条抛物线B.它的开口向上,且关于y轴对称C.它的顶点是抛物线的最高点D.它与y=-3x2的图象关于x轴对称C2.下列函数中,y总随x增大而减小的是( ) A.y=4x B.y=-4x C.y=x-4 D.y=x2B3.若抛物线y=ax2 (a ≠ 0),过点(-1,2).(1)则a的值是 ;(2)对称轴是 ,开口 .(3)顶点坐标是 ,顶点是抛物线上的最 值 . 抛物线在x轴的 方(除顶点外).(4) 若A(x1,y1),B(x2,y2)在这条抛物线上,且x14. 已知函数 是二次函数, 且开口向上.(1)求m的值;(2)求出二次函数的解析式?(3)写出此函数的增减性? 5、根据二次函数 的图像的性质,回答下列问题:(1)如果点P在抛物线 上,那么点Q也在这条抛物线上吗?为什么?(2)当 时,设自变量,的对应值分别为 , ,当 时,必有 吗?为什么?(1)在,因为此二次函数是关于y轴对称的(2)存在这样的关系,因为当a<0时,在y轴右方随着x的增大而减小
课堂小结
y
x
O
x
y
O
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
22.1.2 二次函数y=ax2的图象和性质 教案
课题 22.1.2 二次函数y=ax2的图象和性质 单元 第22单元 学科 数学 年级 九年级(上)
学习目标 1.能够用描点法画函数的图象,并能根据图象认识和理解其性质.2.初步建立二次函数表达式与图象之间的联系,体会数与形结合与转化.
重点 1.理解并掌握二次函数y=ax2的性质.2.掌握二次项系数a的作用.
难点 理解并掌握二次函数y=ax2的性质.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题 复习回顾:1.画函数图象的方法和步骤?方法:描点法;步骤:列表——描点——连线;列表:注意自变量的取值范围;描点:先建系,根据表格确定点的坐标;连线:用光滑的曲线连接.探究二次函数y = x2的图象和性质用描点法画二次函数 y = x2 的图象解:(1) 列表(2) 描点(3) 连线x...-2-1012...y...41014... y y=x2 o x观察二次函数 y=x2 的图象,回答下面问题:二次函数y=x2 的图象是抛物线;开口向上;轴对称图形,对称轴为y轴抛物线与对称轴的交点叫做顶点,y=x2的顶点为(0,0),顶点是最低点;有最小函数值,当x=0时,y最小=0在对称轴y轴的左侧,y随x的增大而减小;在对称轴y轴的左侧,y随x的增大而增大.以上(2)—(6)是函数y=x2的性质. 思考自议回顾一次函数、正比例函数的图象和性质以及画函数图象的方法及步骤. 通过自学、交流和探究,总结规律.
讲授新课 提炼概念 归纳总结:a>0,开口向上,对称轴为y轴;顶点(0、0);函数值有最小值;增减性:在对称轴y轴左侧,y随x的增大而减小,在y轴右侧,y随x的增大而增大.a<0,开口向下,对称轴为y轴;顶点(0、0);函数值有最大值;增减性:在对称轴y轴左侧,y随x的增大而增大,在y轴右侧,y随x的增大而减小.|a|越大,抛物线的开口越小.a>0图象 a<0图象三、典例精讲例1 在同一直角坐标系中画出函数和y=2x2的图象解:(1) 列表x...-2-1012......20.500.52...y=2x2...82028...(2) 描点(3) 连线 观察上面的图象,类比 y=x2的图象和性质,说一说和 y=2x2的图象和性质?和y=2x2的图象都是抛物线. 性质:(1)开口向上;(2)对称轴是y轴;(3)顶点是(0,0);(4)顶点是抛物线的最低点;(5)当x=0时,抛物线有最小函数值y=0;(6)在对称轴y轴左侧,y随x的增大而减小,在对称轴y轴右侧,y随x的增大而增大.思考: y=x2,和y=2x2的图象和性质有什么相同点和不同点 相同点:图象都是抛物线,开口方向、对称轴、顶点、最小值、增减性、对称性都相同;不同点:解析式中的a值不同,图象的开口大小不同.小结:a>0,a越大,抛物线的开口越小.小结:a>0时,二次函数y=ax2的图象和性质:图象都是抛物线,性质:(1)开口方向:开口向上;. (2)开口大小:a越大,抛物线的开口越小; (3)轴对称图形,对称轴为y轴;(4)顶点(0、0); (5)当x=0时二次函数的函数值有最小值为y=0; (6)增减性:在对称轴y轴左侧,y随x的增大而减小,在对称轴y轴右侧,y随x的增大而增大.探究:画出 y= -x2,和 y= -2x2的图象,并说出它们的性质. 图象都是抛物线,性质:(1)开口向下;. (2)对称轴为y轴; (3)顶点(0、0); (4)函数值有最大值; (5)增减性:在对称轴y轴左侧,y随x的增大而增大,在y轴右侧,y随x的增大而减小.不同点:解析式中的a值不同,图象的开口大小不同.小结:a<0,|a|越大,抛物线的开口越小. 体会数形结合的数学思想,结合图形探究性质,为下面探究y = ax2的图象和性质奠定基础. 从具体问题到一般规律获得二次函数y =a x2的性质.
课堂检测 四、巩固训练 1. 关于二次函数y=3x2的图象,下列说法错误的是( )A.它是一条抛物线B.它的开口向上,且关于y轴对称C.它的顶点是抛物线的最高点D.它与y=-3x2的图象关于x轴对称C2.下列函数中,y总随x增大而减小的是( ) A.y=4x B.y=-4x C.y=x-4 D.y=x2B3.若抛物线y=ax2 (a ≠ 0),过点(-1,2).(1)则a的值是 ;(2)对称轴是 ,开口 .(3)顶点坐标是 ,顶点是抛物线上的最 值 . 抛物线在x轴的 方(除顶点外).(4) 若A(x1,y1),B(x2,y2)在这条抛物线上,且x1
课堂小结
y
x
O
x
y
O
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
