2021-2022学年冀教版数学七年级下册9.2.1三角形内角和同步巩固练习题(word版、无答案)
文档属性
| 名称 | 2021-2022学年冀教版数学七年级下册9.2.1三角形内角和同步巩固练习题(word版、无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 330.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 18:30:04 | ||
图片预览

文档简介
9.2.1 三角形内角和
利用下面的方法可以说明三角形的内角和等于 180°,请完成说理过程. 已知:△ABC.
说明:∠A+∠B+∠C=180°.
利用如图所示的拼图说明三角形内角和定理. 已知:△ABC.
说明:∠A+∠B+∠C=180°.
如图,在△ABC 中,∠B=40°,∠A=90°,分别延长 BC 到点 D,延长 AC 到点 E, 则∠DCE 的度数为( )
A.50° B.40° C.30° D.130°
如图,墙上钉着三根木条 a,b,c,量得∠1=70°,∠2=100°,那么木条 a,b 所在直线所夹的锐角是( )
A.5° B.10° C.30° D.70°
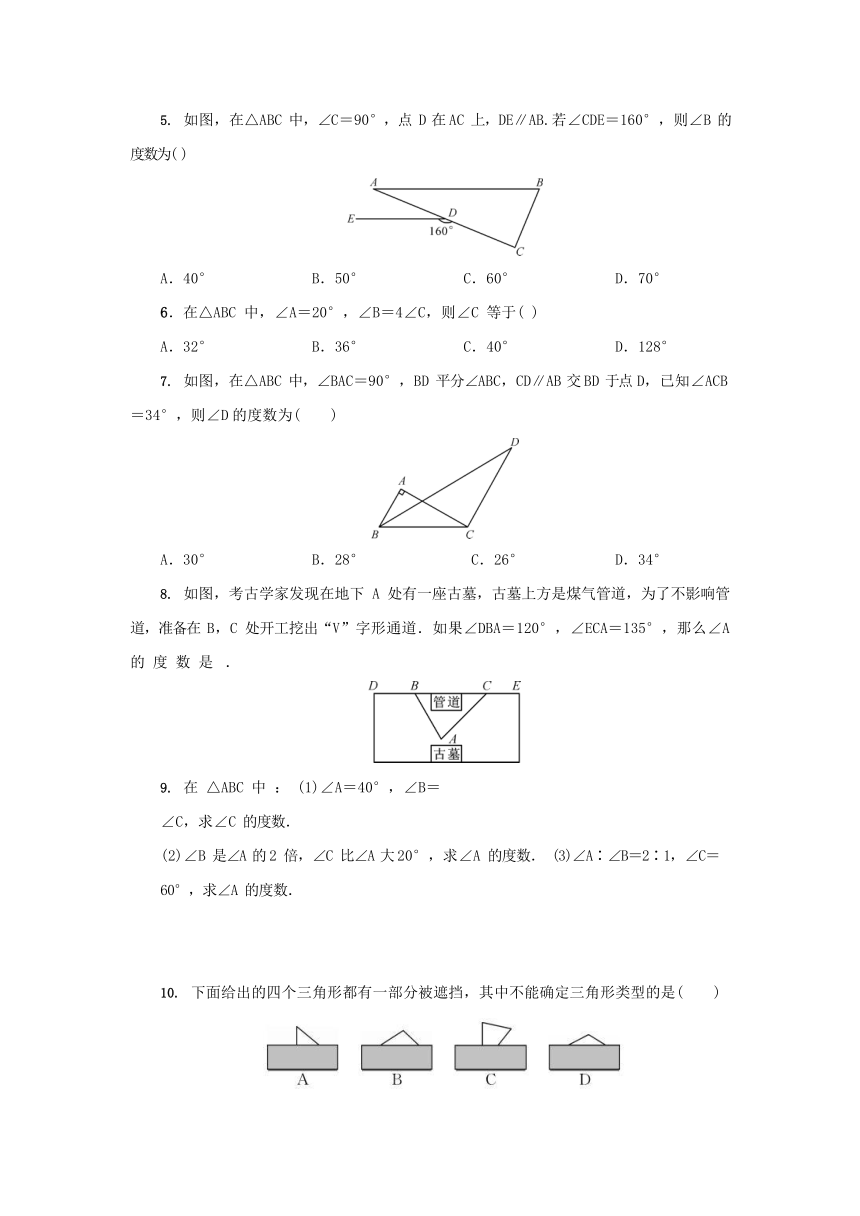
如图,在△ABC 中,∠C=90°,点 D 在 AC 上,DE∥AB.若∠CDE=160°,则∠B 的度数为( )
A.40° B.50° C.60° D.70°
6.在△ABC 中,∠A=20°,∠B=4∠C,则∠C 等于( )
A.32° B.36° C.40° D.128°
如图,在△ABC 中,∠BAC=90°,BD 平分∠ABC,CD∥AB 交 BD 于点 D,已知∠ACB
=34°,则∠D 的度数为( )
A.30° B.28° C.26° D.34°
如图,考古学家发现在地下 A 处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在 B,C 处开工挖出“V”字形通道.如果∠DBA=120°,∠ECA=135°,那么∠A 的 度 数 是 .
在 △ABC 中 : (1)∠A=40°,∠B=∠C,求∠C 的度数.
(2)∠B 是∠A 的 2 倍,∠C 比∠A 大 20°,求∠A 的度数. (3)∠A∶∠B=2∶1,∠C=60°,求∠A 的度数.
下面给出的四个三角形都有一部分被遮挡,其中不能确定三角形类型的是( )
如图,AE 平分∠BAC,CE 平分∠ACD,且 AB∥CD,则∠AEC 等于( )
A.60° B.80° C.100° D.90°
将一副三角尺按如图摆放,点 E 在 AC 上,点 D 在 BC 的延长线上,EF∥BC,∠B
=∠EDF=90°,∠A=45°,∠F=60°,则∠CED 的度数是( )
A.15° B.20° C.25° D.30°
如 图 , 在 △ABC 中 ,∠A=70°,D 是 △ABC 内 一 点 . 若 ∠ABD=30°,∠ACD=25°,则∠BDC= .
如图,将△ABC 沿着平行于 BC 的直线 DE 折叠,点 A 落到点 A′处.若∠C=125°,
∠A=20°,则∠BDA′的度数为 .
15.(教材 P105 习题 B 组 T1 变式)如图所示,在△ABC 中,D 在 AC 上,连接 BD,且∠ ABC=∠C=∠1,∠A=∠3,求∠A 的度数.
16.问题情景:如图 1,在同一平面内,点 B 和点 C 分别位于一块直角三角板 PMN 的两条直角边 PM,PN 上,点 A 与点 P 在直线 BC 的同侧,若点 P 在△ABC 内部,试问∠ABP,∠ ACP 与∠A 的大小是否满足某种确定的数量关系?
特殊探究:若∠A=55°,则∠ABC+∠ACB= 度,∠PBC+∠PCB= 度,
∠ABP+∠ACP= 度.
类比探索:请猜想∠ABP+∠ACP 与∠A 的关系,并说明理由.
类比延伸:改变点 A 的位置,使点 P 在△ABC 外,其他条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出∠ABP,∠ACP 与∠A 满足的数量关系式.
利用下面的方法可以说明三角形的内角和等于 180°,请完成说理过程. 已知:△ABC.
说明:∠A+∠B+∠C=180°.
利用如图所示的拼图说明三角形内角和定理. 已知:△ABC.
说明:∠A+∠B+∠C=180°.
如图,在△ABC 中,∠B=40°,∠A=90°,分别延长 BC 到点 D,延长 AC 到点 E, 则∠DCE 的度数为( )
A.50° B.40° C.30° D.130°
如图,墙上钉着三根木条 a,b,c,量得∠1=70°,∠2=100°,那么木条 a,b 所在直线所夹的锐角是( )
A.5° B.10° C.30° D.70°
如图,在△ABC 中,∠C=90°,点 D 在 AC 上,DE∥AB.若∠CDE=160°,则∠B 的度数为( )
A.40° B.50° C.60° D.70°
6.在△ABC 中,∠A=20°,∠B=4∠C,则∠C 等于( )
A.32° B.36° C.40° D.128°
如图,在△ABC 中,∠BAC=90°,BD 平分∠ABC,CD∥AB 交 BD 于点 D,已知∠ACB
=34°,则∠D 的度数为( )
A.30° B.28° C.26° D.34°
如图,考古学家发现在地下 A 处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在 B,C 处开工挖出“V”字形通道.如果∠DBA=120°,∠ECA=135°,那么∠A 的 度 数 是 .
在 △ABC 中 : (1)∠A=40°,∠B=∠C,求∠C 的度数.
(2)∠B 是∠A 的 2 倍,∠C 比∠A 大 20°,求∠A 的度数. (3)∠A∶∠B=2∶1,∠C=60°,求∠A 的度数.
下面给出的四个三角形都有一部分被遮挡,其中不能确定三角形类型的是( )
如图,AE 平分∠BAC,CE 平分∠ACD,且 AB∥CD,则∠AEC 等于( )
A.60° B.80° C.100° D.90°
将一副三角尺按如图摆放,点 E 在 AC 上,点 D 在 BC 的延长线上,EF∥BC,∠B
=∠EDF=90°,∠A=45°,∠F=60°,则∠CED 的度数是( )
A.15° B.20° C.25° D.30°
如 图 , 在 △ABC 中 ,∠A=70°,D 是 △ABC 内 一 点 . 若 ∠ABD=30°,∠ACD=25°,则∠BDC= .
如图,将△ABC 沿着平行于 BC 的直线 DE 折叠,点 A 落到点 A′处.若∠C=125°,
∠A=20°,则∠BDA′的度数为 .
15.(教材 P105 习题 B 组 T1 变式)如图所示,在△ABC 中,D 在 AC 上,连接 BD,且∠ ABC=∠C=∠1,∠A=∠3,求∠A 的度数.
16.问题情景:如图 1,在同一平面内,点 B 和点 C 分别位于一块直角三角板 PMN 的两条直角边 PM,PN 上,点 A 与点 P 在直线 BC 的同侧,若点 P 在△ABC 内部,试问∠ABP,∠ ACP 与∠A 的大小是否满足某种确定的数量关系?
特殊探究:若∠A=55°,则∠ABC+∠ACB= 度,∠PBC+∠PCB= 度,
∠ABP+∠ACP= 度.
类比探索:请猜想∠ABP+∠ACP 与∠A 的关系,并说明理由.
类比延伸:改变点 A 的位置,使点 P 在△ABC 外,其他条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出∠ABP,∠ACP 与∠A 满足的数量关系式.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
