11.5几何证明举例(1) 课件

课件15张PPT。11.5(1)几何证明举例有关全等三角形的证明 1.到目前为止，我们学习了哪些判定三角形全等的方法?分别是什么？ASA,AAS,SAS,SSS2.在这4种判定三角形全等的方法的方法中，哪几个是公理？ASA,SAS,SSS
3.全等三角形的性质是什么?全等三角形的对应边相等，对应角相等4.证明全等三角形常用的隐含条件是什么？（1）公共边（2）公共角（3）对顶角相等教学目标1、证明并掌握定理：两角及其中一角的对边分别对应相等的两个三角形全等。
2、会运用全等三角形的性质和判定，证明有关的问题．
3、养成善于思考，善于探究，善于推理，言必有据的好习惯。
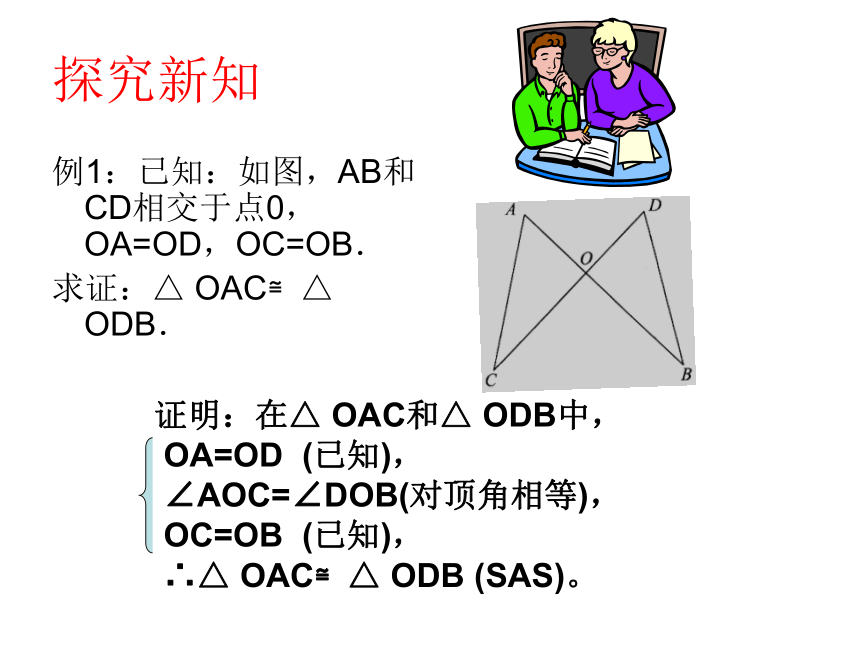
4、经历命题的证明过程，逐步学会分别从题设和结论出发，寻求论证思路的综合分析方法。探究新知例1：已知：如图，AB和CD相交于点0，OA=OD，OC=OB．
求证：△ OAC≌△ ODB．证明：在△ OAC和△ ODB中，
OA=OD (已知)，
∠AOC=∠DOB(对顶角相等)，
OC=OB (已知)，
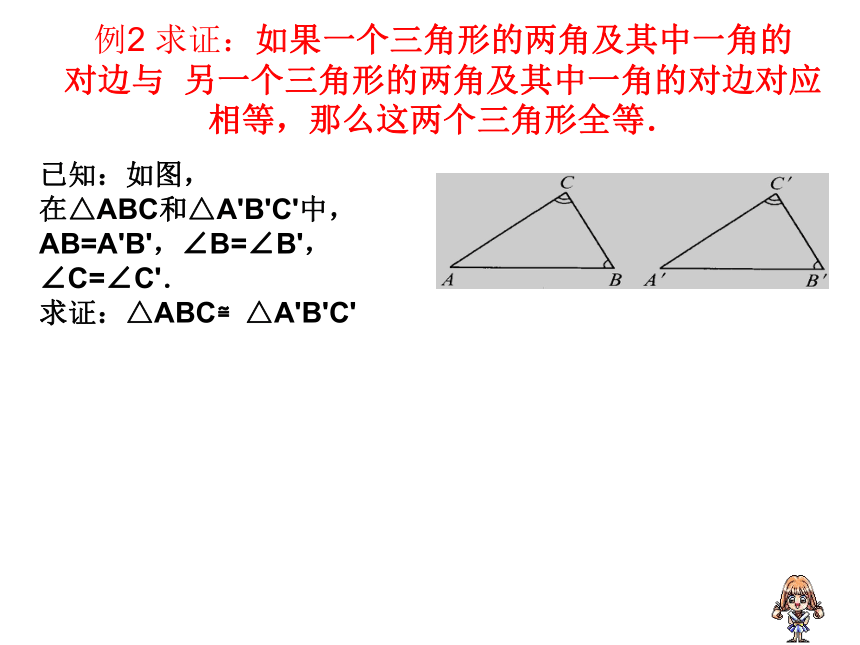
∴△ OAC≌△ ODB (SAS)。例2 求证：如果一个三角形的两角及其中一角的 对边与 另一个三角形的两角及其中一角的对边对应 相等，那么这两个三角形全等．已知：如图，
在△ABC和△A'B'C'中，
AB=A'B'，∠B=∠B'，∠C=∠C'．
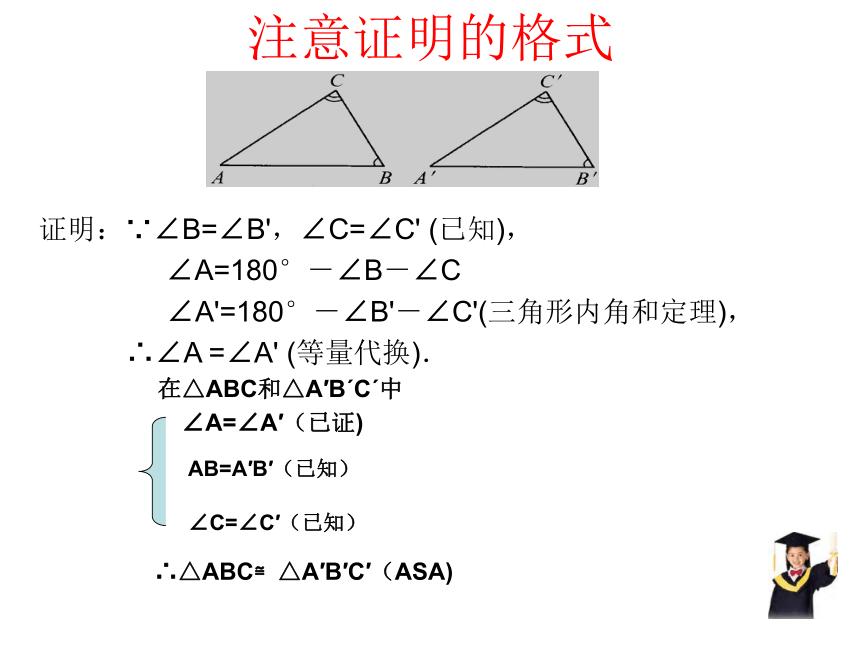
求证：△ABC≌△A'B'C'证明：∵∠B=∠B'，∠C=∠C' (已知)，
∠A=180°－∠B－∠C
∠A'=180°－∠B'－∠C'(三角形内角和定理)，
∴∠A =∠A' (等量代换)．注意证明的格式在△ABC和△A′BˊCˊ中∠A=∠A′（已证)AB=A′B′（已知）∠C=∠C′（已知）∴△ABC≌△A′B′C′（ASA)温馨提示
（1）全等三角形的“角角边”判定方法．它不是公理，而是一个定理，其正确性，需要通过证明．
（2）“角角边”定理是应用三角形内角和定理及公理“ASA”证明的．
（3）判定三角形全等的根据：公理SAS、ASA、SSS及定理AAS．全等三角形的重要作用在于利用它的性质证明线段相等或角相等，是一个转化的“媒介”1.如图，BD=CD,∠ADB=∠ADC
求证：∠B=∠C小试牛刀证明：在△ADB和△ADC中AD=AD（ ）∠ADC=∠ADB（ ）
BD=CD（ ）∴△ADB≌△ADC( )∴∠B=∠C( )公共边已知已知SAS全等三角形对应角相等温馨提示：
在证明三角形全等后，进一步利用全等三角形的性质，证明线段相等或角相等， 2.已知：AB与CD相交于点O，
∠A=∠C，OA=OC，
求证：△AOD≌△COB.
证明：在△AOD和△COB中∠A=∠C(已知）OA=OC（已知）∠AOD=∠COB(对顶角相等）∴△AOD≌△COB(ASA） 看我有多棒！1.已知：如图，AB=AC,
∠B=∠C．
求证：BD=CE．证明：在△ABD和△ACE中∠A=∠A（公共角）AB=AC（已知）∠B=∠C（已知）∴△ABD≌△ACE（ASA）∴BD=CE(全等三角形的对应边相等）2.如图AB=AC，若使△ADC≌△AEB， 则还需要什么条件？
补充上条件后，并给出根据。你行，我也行更上一城楼求证：线段垂直平分线上的点到这条线段两端点的距离相等．已知：点C在线段AB的垂直平分线MN上
求证:AC=BC证明：∵MN是线段AB的垂直平分线（已知）
∴AO=BO,∠AOC=∠BOC=90°(垂直平分线的定义）在△AOC和△BOC中AO=BO (已证）∠AOC=∠BOC(已证）CO=CO（公共边）∴△AOC≌△BOC(ASA)∴AC=BC（全等三角形的对应边相等)小结判定三角形全等的方法有：
“ASA”、“ AAS ”、 “SAS”、“SSS” 。
利用三角形全等可以得到线段相等和角相等。作业课本P135页
习题11.5 A组 1. 2. 3.题
谢谢同学们的精彩表现再见谢谢老师的指导