6.2立方根 课件
图片预览








文档简介
课件22张PPT。6.2 立方根2013年3月28日
七年级数学备课组 本节在研究了平方根的内容后,研究立方根的概念和求法.类比平方根研究立方根,分析它们之间的联系与区别,在复习巩固平方根概念和求法的同时,学习立方根的概念和求法.课件说明学习目标:
(1)了解立方根的概念.
(2)会求一些数的立方根.
学习重点:
引导学生类比平方根学习立方根的概念和求法.课件说明 1.复习引入 你还记得什么是平方根吗?平方根具有什么特任征? 正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根. 如果一个数的平方等于 ,那么这个数就叫做 的平方根(也叫做二次方根).即若 那么 叫做 的平方根.要制作一种容积为 的正方体形状的包装箱,这种包装箱的棱长应该是多? 2.探究新知如果设这种包装箱的棱长为x m,那么可以得到什么等式?你还记得正方体的体积与棱长有什么关系吗?你能类比平方根的定义给出立方根的定义吗? 2.探究新知立方根的定义:如果一个数的立方等于 ,那么这个数就叫做 的立方根(也叫做三次方根).
即若 那么 叫做 的立方根. 求一个数 的立方根的运算叫做开立方.根据立方根的意义填空.你能发现正数、0和负数的立方根各有什么特点吗?2.探究新知因为 ,所以8的立方根是( );
因为 ,所以0.064的立方根是( );
因为 ,所以0的立方根是( );
因为 ,所以-8的立方根是( );
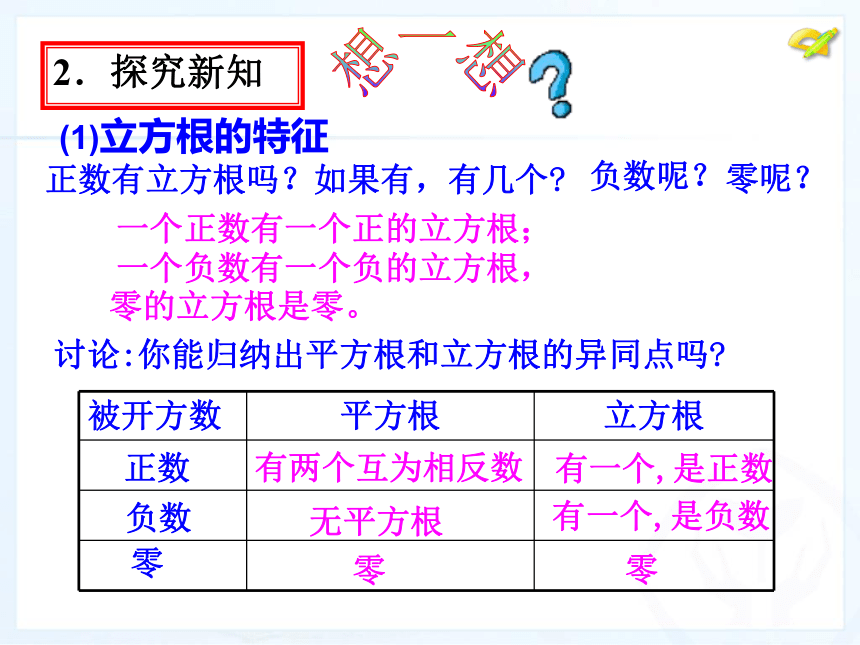
因为 ,所以 的立方根是( ).2.探究新知正数有立方根吗?如果有,有几个?想一想负数呢?零呢?一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。(1)立方根的特征讨论:你能归纳出平方根和立方根的异同点吗?有两个互为相反数有一个,是正数无平方根零有一个,是负数零正数负数零一个数 的立方根,记作 ,
读作:“三次根号a”,
其中a叫被开方数,3叫根指数,3不能省略.2.探究新知填空,你能发现其中的规律吗?2.探究新知因为 = ,
所以
因为
所以 一般地 .-2==-2-3-33.运用新知例1 求下列各数的立方根:3.运用新知例2 求下列各式的值 :例3.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=125解:∴x=7∴x-1=5
X=6(3)(4)∴X=66∴x=8探究先填写下表,再回答问题:0.010.1110100从上面表格中你发现什么?归纳: 被开方数扩大(缩小)1000倍时,它的立方根扩大(缩小)10倍.1.1110600.62如果一个数的平方等于a,
那么这个数就叫a的平方根。 如果一个数的立方等于a,
那么这个数就叫a的立方根。 有两个平方根,互为相反数 有一个平方根,是0 没有平方根 求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。 ,其中a 是被开方数,
2是根指数(省略) 求一个数的立方根的运算
叫开立方;开立方与立方
是互逆运算。 有一个立方根,也是负数 有一个立方根,是0 有一个立方根,也是正数 ,其中a 是被开方数,
3是根指数(不能省略) 平方根和立方根的对比4.归纳总结1:什么是立方根?如何求一个数的立方根?2:我们研究立方根的方法与研究平方根的方法之间有什么联系? 1.(1)1的平方根是_____;立方根为____;
算术平方根为_________.
(2)平方根是它本身的数是__________.
(3)立方根是其本身的数是___________.
(4)算术平方根是其本身的数是________.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:±1110±1 , 01 , 0-2±2-20.06993-324.6-0.150722803280003、下列各组数中互为相反数的一组是( )4、要使 成立,则a必须满足A( D ) 的整数部分是( ),小数部分是( ) 的整数部分是( ),小数部分是( )5.6、比较大小5.布置作业教科书 习题6.2 第1、3、5题
七年级数学备课组 本节在研究了平方根的内容后,研究立方根的概念和求法.类比平方根研究立方根,分析它们之间的联系与区别,在复习巩固平方根概念和求法的同时,学习立方根的概念和求法.课件说明学习目标:
(1)了解立方根的概念.
(2)会求一些数的立方根.
学习重点:
引导学生类比平方根学习立方根的概念和求法.课件说明 1.复习引入 你还记得什么是平方根吗?平方根具有什么特任征? 正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根. 如果一个数的平方等于 ,那么这个数就叫做 的平方根(也叫做二次方根).即若 那么 叫做 的平方根.要制作一种容积为 的正方体形状的包装箱,这种包装箱的棱长应该是多? 2.探究新知如果设这种包装箱的棱长为x m,那么可以得到什么等式?你还记得正方体的体积与棱长有什么关系吗?你能类比平方根的定义给出立方根的定义吗? 2.探究新知立方根的定义:如果一个数的立方等于 ,那么这个数就叫做 的立方根(也叫做三次方根).
即若 那么 叫做 的立方根. 求一个数 的立方根的运算叫做开立方.根据立方根的意义填空.你能发现正数、0和负数的立方根各有什么特点吗?2.探究新知因为 ,所以8的立方根是( );
因为 ,所以0.064的立方根是( );
因为 ,所以0的立方根是( );
因为 ,所以-8的立方根是( );
因为 ,所以 的立方根是( ).2.探究新知正数有立方根吗?如果有,有几个?想一想负数呢?零呢?一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。(1)立方根的特征讨论:你能归纳出平方根和立方根的异同点吗?有两个互为相反数有一个,是正数无平方根零有一个,是负数零正数负数零一个数 的立方根,记作 ,
读作:“三次根号a”,
其中a叫被开方数,3叫根指数,3不能省略.2.探究新知填空,你能发现其中的规律吗?2.探究新知因为 = ,
所以
因为
所以 一般地 .-2==-2-3-33.运用新知例1 求下列各数的立方根:3.运用新知例2 求下列各式的值 :例3.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=125解:∴x=7∴x-1=5
X=6(3)(4)∴X=66∴x=8探究先填写下表,再回答问题:0.010.1110100从上面表格中你发现什么?归纳: 被开方数扩大(缩小)1000倍时,它的立方根扩大(缩小)10倍.1.1110600.62如果一个数的平方等于a,
那么这个数就叫a的平方根。 如果一个数的立方等于a,
那么这个数就叫a的立方根。 有两个平方根,互为相反数 有一个平方根,是0 没有平方根 求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。 ,其中a 是被开方数,
2是根指数(省略) 求一个数的立方根的运算
叫开立方;开立方与立方
是互逆运算。 有一个立方根,也是负数 有一个立方根,是0 有一个立方根,也是正数 ,其中a 是被开方数,
3是根指数(不能省略) 平方根和立方根的对比4.归纳总结1:什么是立方根?如何求一个数的立方根?2:我们研究立方根的方法与研究平方根的方法之间有什么联系? 1.(1)1的平方根是_____;立方根为____;
算术平方根为_________.
(2)平方根是它本身的数是__________.
(3)立方根是其本身的数是___________.
(4)算术平方根是其本身的数是________.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:±1110±1 , 01 , 0-2±2-20.06993-324.6-0.150722803280003、下列各组数中互为相反数的一组是( )4、要使 成立,则a必须满足A( D ) 的整数部分是( ),小数部分是( ) 的整数部分是( ),小数部分是( )5.6、比较大小5.布置作业教科书 习题6.2 第1、3、5题
