苏科版数学七年级下册同步课件:11.3 不等式的基本性质(共14张PPT)
文档属性
| 名称 | 苏科版数学七年级下册同步课件:11.3 不等式的基本性质(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 167.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
第11章 一元一次不等式
11.3 不等式的基本性质
知识回顾
前面我们已经学习过等式的基本性质
(1)等式的两边加或减同一个数(或式子),等式仍然成立.
(2)等式的两边乘或除以同一个数(除数不 为0),等式仍然成立.
猜想 :不等式也具有同样的性质吗?
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0).
合作探究1:
弟弟今年a岁,哥哥今年b岁,下面是弟弟和哥哥的一段对话:
①哥哥说:“再过3年我还是比你大”;
②弟弟说:“3年前你也比我大”.
他们的判断对吗?为什么?你能写出相应的不等式吗?
获取新知
a+3>b+3
a-3>b-3
如果a>b,那么a+c>b+c,a-c>b-c.
归纳小结
不等式的基本性质1:
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
用字母表示:
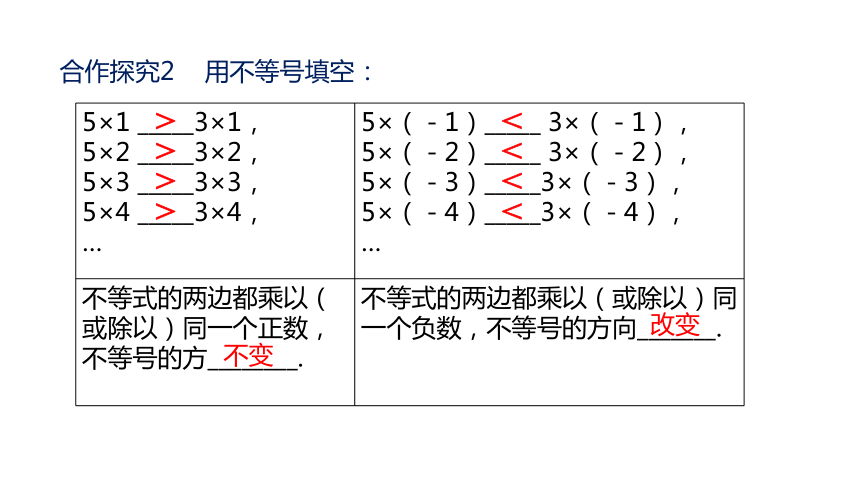
5×1 _____3×1, 5×2 _____3×2, 5×3 _____3×3, 5×4 _____3×4, … 5×(-1)_____ 3×(-1),
5×(-2)_____ 3×(-2),
5×(-3)_____3×(-3),
5×(-4)_____3×(-4),
…
不等式的两边都乘以(或除以)同一个正数,不等号的方________. 不等式的两边都乘以(或除以)同一个负数,不等号的方向_______.
合作探究2 用不等号填空:
不变
改变
>
>
>
>
<
<
<
<
归纳小结
如果a>b,c>0,那么ac____bc(或 ).
>
如果a>b,c<0,那么ac ____bc(或 ).
<
不等式的基本性质2:
不等式的两边都乘(或除以)同一个正数,不等号的方向不变;
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
用字母表示:
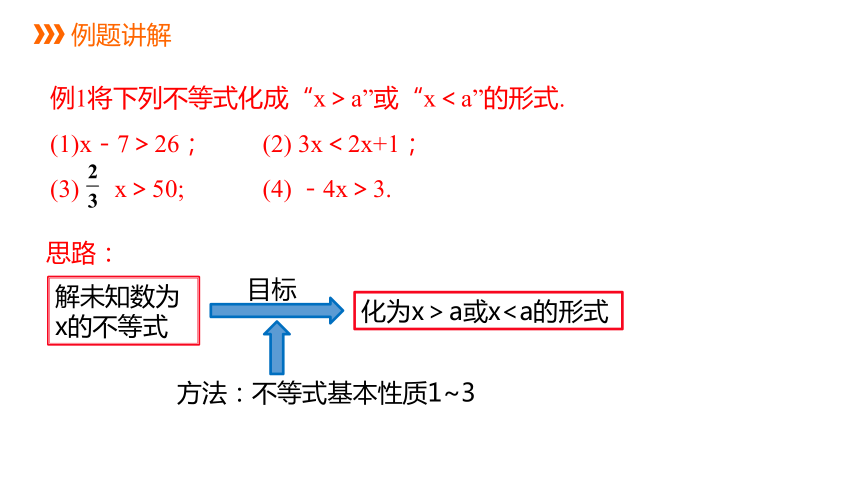
例题讲解
例1将下列不等式化成“x>a”或“x<a”的形式.
(1)x-7>26; (2) 3x<2x+1;
(3) x>50; (4) -4x>3.
解未知数为x的不等式
化为x>a或x目标
方法:不等式基本性质1~3
思路:
解:(1)根据不等式的性质1,不等式两边加7, 不等号的方向不变,所以x-7+7>26+7,即x>33.
(2)根据不等式的性质1,不等式两边减2x,不等号的方向不变,所以3x-2x<2x+1-2x, 即x<1.
(1)x-7>26; (2) 3x<2x+1;
(3)根据不等式的性质2, 不等式两边乘 . 不等号的方向不变,
所以 即x>75.
(3) x>50;
(4) -4x>3.
(4)根据不等式的性质2, 不等式两边除以-4, 不等号的方向改变,所以
D
随堂演练
2.已知a>b,用“>”或“<”号填空:
(1)a+2 _____ b+2; (2)a-5 _____b-5;
(3) 6a _____ 6b; (4) -a _____-b;
(5)2a-3 _____ 2b-3;
(6)-4a+3 _____-4b+3.
>
>
>
<
>
<
3.说出下列不等式变形的依据:
(1)由x-1>2,得x>3;
(2)由2x>-4,得x>-2;
(3)由-0.5x <-1,得x>2;
(4)由3x<x,得2x<0.
不等式的基本性质1
不等式的基本性质2
不等式的基本性质2
不等式的基本性质1
解:(1)不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-3-2x,即 x < -3.
(2)-x< 根据不等式的基本性质3,两边都除以-1,得x>-
(3) x≤3. 根据不等式的基本性质2,两边都乘2,得x≤6.
4.将下列不等式化成“x>a”或“x<a”的形式:
(1) 3x < 2x -3 ; (2)-x< ; (3) x<3.1
课堂小结
不等式的基本性质
不等式基本性质2
如果 那么
如果 那么
应用性质对不等式简单变形
不等式的基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
第11章 一元一次不等式
11.3 不等式的基本性质
知识回顾
前面我们已经学习过等式的基本性质
(1)等式的两边加或减同一个数(或式子),等式仍然成立.
(2)等式的两边乘或除以同一个数(除数不 为0),等式仍然成立.
猜想 :不等式也具有同样的性质吗?
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0).
合作探究1:
弟弟今年a岁,哥哥今年b岁,下面是弟弟和哥哥的一段对话:
①哥哥说:“再过3年我还是比你大”;
②弟弟说:“3年前你也比我大”.
他们的判断对吗?为什么?你能写出相应的不等式吗?
获取新知
a+3>b+3
a-3>b-3
如果a>b,那么a+c>b+c,a-c>b-c.
归纳小结
不等式的基本性质1:
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
用字母表示:
5×1 _____3×1, 5×2 _____3×2, 5×3 _____3×3, 5×4 _____3×4, … 5×(-1)_____ 3×(-1),
5×(-2)_____ 3×(-2),
5×(-3)_____3×(-3),
5×(-4)_____3×(-4),
…
不等式的两边都乘以(或除以)同一个正数,不等号的方________. 不等式的两边都乘以(或除以)同一个负数,不等号的方向_______.
合作探究2 用不等号填空:
不变
改变
>
>
>
>
<
<
<
<
归纳小结
如果a>b,c>0,那么ac____bc(或 ).
>
如果a>b,c<0,那么ac ____bc(或 ).
<
不等式的基本性质2:
不等式的两边都乘(或除以)同一个正数,不等号的方向不变;
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
用字母表示:
例题讲解
例1将下列不等式化成“x>a”或“x<a”的形式.
(1)x-7>26; (2) 3x<2x+1;
(3) x>50; (4) -4x>3.
解未知数为x的不等式
化为x>a或x
方法:不等式基本性质1~3
思路:
解:(1)根据不等式的性质1,不等式两边加7, 不等号的方向不变,所以x-7+7>26+7,即x>33.
(2)根据不等式的性质1,不等式两边减2x,不等号的方向不变,所以3x-2x<2x+1-2x, 即x<1.
(1)x-7>26; (2) 3x<2x+1;
(3)根据不等式的性质2, 不等式两边乘 . 不等号的方向不变,
所以 即x>75.
(3) x>50;
(4) -4x>3.
(4)根据不等式的性质2, 不等式两边除以-4, 不等号的方向改变,所以
D
随堂演练
2.已知a>b,用“>”或“<”号填空:
(1)a+2 _____ b+2; (2)a-5 _____b-5;
(3) 6a _____ 6b; (4) -a _____-b;
(5)2a-3 _____ 2b-3;
(6)-4a+3 _____-4b+3.
>
>
>
<
>
<
3.说出下列不等式变形的依据:
(1)由x-1>2,得x>3;
(2)由2x>-4,得x>-2;
(3)由-0.5x <-1,得x>2;
(4)由3x<x,得2x<0.
不等式的基本性质1
不等式的基本性质2
不等式的基本性质2
不等式的基本性质1
解:(1)不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-3-2x,即 x < -3.
(2)-x< 根据不等式的基本性质3,两边都除以-1,得x>-
(3) x≤3. 根据不等式的基本性质2,两边都乘2,得x≤6.
4.将下列不等式化成“x>a”或“x<a”的形式:
(1) 3x < 2x -3 ; (2)-x< ; (3) x<3.1
课堂小结
不等式的基本性质
不等式基本性质2
如果 那么
如果 那么
应用性质对不等式简单变形
不等式的基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
