苏科版数学七年级下册同步课件:11.4 第2课时 去分母解一元一次不等式(共12张PPT)
文档属性
| 名称 | 苏科版数学七年级下册同步课件:11.4 第2课时 去分母解一元一次不等式(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 158.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 16:15:32 | ||
图片预览





文档简介
(共12张PPT)
第11章 一元一次不等式
11.4 第2课时 去分母解一元一次不等式
例1 解不等式 ≥ ,并把它的解集在数轴上表示出来.
例题讲解
解:不等式两边同乘以2,得2(2x-1)≥3x-1 .
去括号,得 4x-2≥3x-1 .
移项,得 4x-3x≥-1+2 .
合并同类项,得 x≥1 .
这个不等式的解集在数轴上的表示如图所示 .
-3
-2
-1
0
1
2
3
4
这就是去分母.
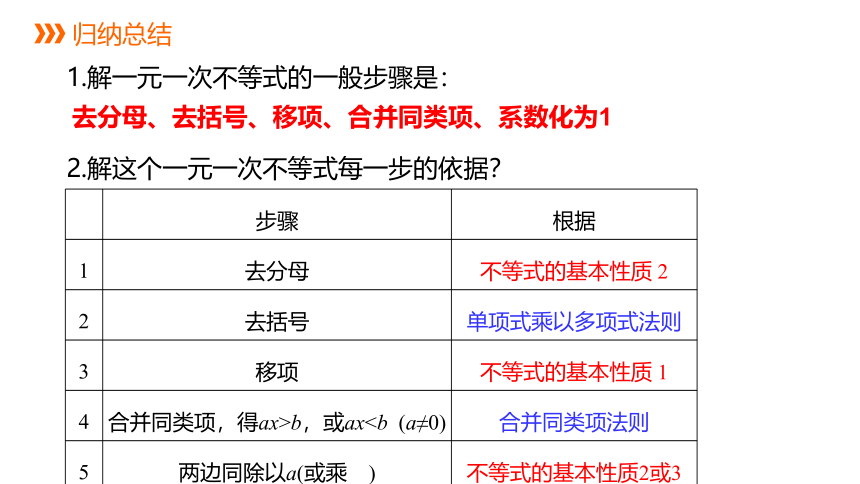
1.解一元一次不等式的一般步骤是:
2.解这个一元一次不等式每一步的依据?
去分母、去括号、移项、合并同类项、系数化为1
归纳总结
步骤 根据
1 去分母 不等式的基本性质 2
2 去括号 单项式乘以多项式法则
3 移项 不等式的基本性质 1
4 合并同类项,得ax>b,或ax5 两边同除以a(或乘 ) 不等式的基本性质2或3
3. 解一元一次方程与解一元一次不等式的区别和联系分别是什么?
联系:
两种解法的步骤相似,一般都经过了去分母、去括号、移项、合并同类项、未知数的系数化为1.
区别:
不等式在去分母和系数化成1时,当两边都乘(或除以)同一个负数时,不等号的方向改变;
而方程两边乘(或除以)同一个负数时,等号不变.
例2 解不等式 < ,并把它的解集在数轴上表示出来.
解:去分母,得6-3(x +6)<2(2x+1) .
去括号,得6-3x- 18<4x+2.
移项,得 -3x-4x<2-6+18.
合并同类项,得-7x <14 .
系数化为1,得x>-2.
这个不等式的解集在数轴上的表示如图所示:
5
-3
-1
1
3
2
4
-2
0
例题讲解
例3 求不等式3(x+1)≥5x-9的正整数解.
分析:求不等式的正整数解,即在原不等式的解集中找出它所包含的“正整数”特殊解;因此先需求出原不等式的解集.
解:∵解不等式3(x+1)≥5x-9得x≤6.
在数轴上表示为:
∴不等式3(x+1)≥5x-9的正整数解为 1,2,3,4,5,6.
注意:在确定特殊解时,一定要注意是否包括端点的值,一般可以结合数轴,形象直观,一目了然.
-1
0
1
2
3
4
5
6
1. 解不等式 ≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
D
随堂演练
2. 解一元一次不等式:
解:去分母,得_____-(x+5)<3x+2.
去括号,得2-________<3x+2.
移项,得-x-_____<2-2+5.
合并同类项,得-4x<5.
系数化为1,得x>________.
2
x-5
3x
-1.25
3. 解下列不等式,并把它们的解集分别表示在数轴上:
(1) (2)
解:(1)去分母,得3(x -1)<2(4x-5) .
去括号,得3x-3 < 8x-10.
移项、合并同类项,得-5x < - 7 .
两边都除以-5,得x> .
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
(2)去分母,得(x +7) -2<3x+2 .
去括号,得x+7- 2 < 3x+2 .
移项、合并同类项,得-2x < - 3 .
两边都除以-2,得x> .
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
(2)
4. 当x取何值时,代数式 与 的值的差大于1?
去分母,得 2(x+4)-3(3x-1)>6.
去括号,得 2x+8-9x+3>6,
合并同类项,得 -7x+11>6.
移项,得 -7x >-5.
解:根据题意,得
两边都除以-7,得
所以,当x取小于 的任何数时,代数式 与 的值的差大于1.
课堂小结
解一元一次不等式的一般步骤
去分母
去括号
移项
合并同类项
系数化为1
第11章 一元一次不等式
11.4 第2课时 去分母解一元一次不等式
例1 解不等式 ≥ ,并把它的解集在数轴上表示出来.
例题讲解
解:不等式两边同乘以2,得2(2x-1)≥3x-1 .
去括号,得 4x-2≥3x-1 .
移项,得 4x-3x≥-1+2 .
合并同类项,得 x≥1 .
这个不等式的解集在数轴上的表示如图所示 .
-3
-2
-1
0
1
2
3
4
这就是去分母.
1.解一元一次不等式的一般步骤是:
2.解这个一元一次不等式每一步的依据?
去分母、去括号、移项、合并同类项、系数化为1
归纳总结
步骤 根据
1 去分母 不等式的基本性质 2
2 去括号 单项式乘以多项式法则
3 移项 不等式的基本性质 1
4 合并同类项,得ax>b,或ax5 两边同除以a(或乘 ) 不等式的基本性质2或3
3. 解一元一次方程与解一元一次不等式的区别和联系分别是什么?
联系:
两种解法的步骤相似,一般都经过了去分母、去括号、移项、合并同类项、未知数的系数化为1.
区别:
不等式在去分母和系数化成1时,当两边都乘(或除以)同一个负数时,不等号的方向改变;
而方程两边乘(或除以)同一个负数时,等号不变.
例2 解不等式 < ,并把它的解集在数轴上表示出来.
解:去分母,得6-3(x +6)<2(2x+1) .
去括号,得6-3x- 18<4x+2.
移项,得 -3x-4x<2-6+18.
合并同类项,得-7x <14 .
系数化为1,得x>-2.
这个不等式的解集在数轴上的表示如图所示:
5
-3
-1
1
3
2
4
-2
0
例题讲解
例3 求不等式3(x+1)≥5x-9的正整数解.
分析:求不等式的正整数解,即在原不等式的解集中找出它所包含的“正整数”特殊解;因此先需求出原不等式的解集.
解:∵解不等式3(x+1)≥5x-9得x≤6.
在数轴上表示为:
∴不等式3(x+1)≥5x-9的正整数解为 1,2,3,4,5,6.
注意:在确定特殊解时,一定要注意是否包括端点的值,一般可以结合数轴,形象直观,一目了然.
-1
0
1
2
3
4
5
6
1. 解不等式 ≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
D
随堂演练
2. 解一元一次不等式:
解:去分母,得_____-(x+5)<3x+2.
去括号,得2-________<3x+2.
移项,得-x-_____<2-2+5.
合并同类项,得-4x<5.
系数化为1,得x>________.
2
x-5
3x
-1.25
3. 解下列不等式,并把它们的解集分别表示在数轴上:
(1) (2)
解:(1)去分母,得3(x -1)<2(4x-5) .
去括号,得3x-3 < 8x-10.
移项、合并同类项,得-5x < - 7 .
两边都除以-5,得x> .
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
(2)去分母,得(x +7) -2<3x+2 .
去括号,得x+7- 2 < 3x+2 .
移项、合并同类项,得-2x < - 3 .
两边都除以-2,得x> .
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
(2)
4. 当x取何值时,代数式 与 的值的差大于1?
去分母,得 2(x+4)-3(3x-1)>6.
去括号,得 2x+8-9x+3>6,
合并同类项,得 -7x+11>6.
移项,得 -7x >-5.
解:根据题意,得
两边都除以-7,得
所以,当x取小于 的任何数时,代数式 与 的值的差大于1.
课堂小结
解一元一次不等式的一般步骤
去分母
去括号
移项
合并同类项
系数化为1
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
