苏科版数学七年级下册同步课件:7.1 第1课时 探索直线平行的条件(1)(共19张PPT)
文档属性
| 名称 | 苏科版数学七年级下册同步课件:7.1 第1课时 探索直线平行的条件(1)(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 16:31:36 | ||
图片预览




文档简介
(共19张PPT)
第7章 平面图形的认识(二)
7.1第1课时 探索直线平行线的条件(1)
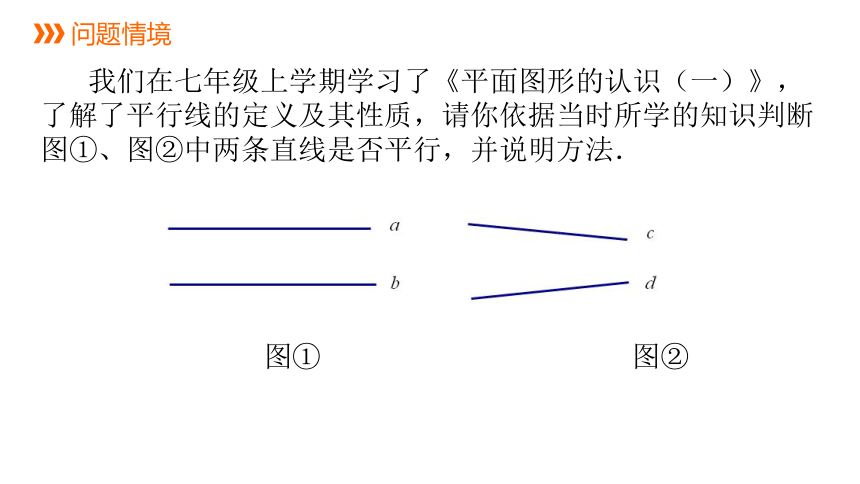
问题情境
我们在七年级上学期学习了《平面图形的认识(一)》,了解了平行线的定义及其性质,请你依据当时所学的知识判断图①、图②中两条直线是否平行,并说明方法.
图① 图②
数学活动
如图,你会过直线l外一点P画已知直线l的平行线吗?
数学活动
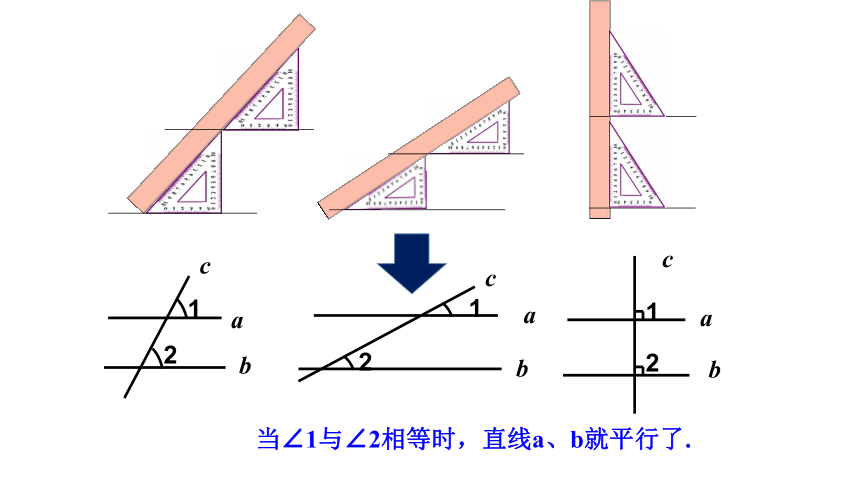
我们可以利用三角板和直尺画平行线:
1
2
a
b
c
1
2
c
a
b
a
b
1
2
c
当∠1与∠2相等时,直线a、b就平行了.
b
a
c
1
2
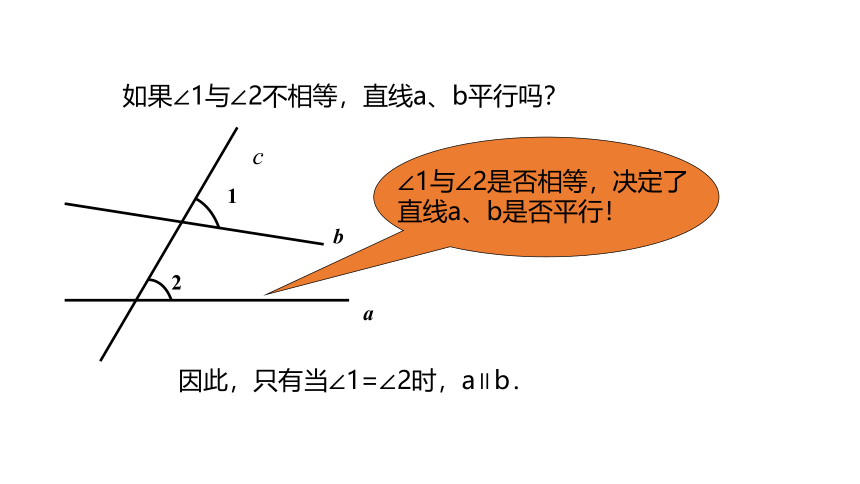
如果∠1与∠2不相等,直线a、b平行吗?
∠1与∠2是否相等,决定了直线a、b是否平行!
因此,只有当∠1=∠2时,a∥b.
1
2
3
4
5
6
8
a
b
7
c
1.∠1、∠2的边所在的直线是哪些直线
2.∠1、∠2的边所在的直线的公共直线是哪条直线
3.∠1、∠2可以看成哪两条直线被第三条直线截成的角
4.∠1、∠2在位置上有何特点
∠1、∠2都在被截两条直线的同一方向,且都在第三条直线的同旁.
获取新知
1
2
3
4
5
6
8
两条直线a、b被第三条直线c所截而成的8个角中,像∠1与∠2这样的一对角称为同位角.
∠1与∠2是由两条直线a、b被直线c所截构成的同位角.
还有其他的同位角吗?
∠3与∠4,∠5与∠6,∠7与∠8也是同位角
a
b
7
c
议一议:
同位角在数量上应具备什么样的条件,才能使对应的直线平行呢?
b
a
1
2
图中,显然a与b不平行,要使a ∥ b,必须∠1=∠2,也就是只要∠1=∠2,那么a ∥ b,而∠1与∠2是直线a、b被直线c所截而得的同位角.
基本事实:“两直线被第三条直线所截,如果同位角相等,那么这两条直线平行.”即“同位角相等,两直线平行.”
c
例题讲解
例 1 如图,∠1=∠C,∠2=∠C,请指出图中互相平行的直线,并说明理由.
A
B
C
D
1
2
解: AB∥CD,AC∥BD.
(1)因为∠1与∠C是AB、CD
被AC截成的同位角,且∠1=∠C,
所以AB∥CD.
(2)因为∠2与∠C是BD、AC
被CD截成的同位角,且∠2=∠C,
所以AC∥BD.
例 2 如图 7—1—2,根据下列条件可以判定哪两条直线互相平行,为什么
(1)∠AEB=∠D; (2) ∠EGF=∠B;
(3)∠DFG=∠A; (4) ∠EGF=∠C.
图 7-1-2
A
解∶(1)BE∥CD.理由∶因为∠AEB=∠D,根据"同位角相等,两直线平行"可得BE∥CD.
(2)CF∥AB.理由∶因为∠EGF=∠B,根据"同位角相等,两直线平行"
可得 CF∥AB.
(3)CF∥AB.理由∶因为∠DFG=∠A,根据"同位角相等,两直线平行"可得 CF∥AB.
(4)BE∥CD.理由∶因为∠EGF=∠C,根据"同位角相等,两直线平行"可得BE∥CD.
D
随堂演练
AB∥CD
同位角相等,两直线平行
1
2
b
c
a
第7章 平面图形的认识(二)
7.1第1课时 探索直线平行线的条件(1)
问题情境
我们在七年级上学期学习了《平面图形的认识(一)》,了解了平行线的定义及其性质,请你依据当时所学的知识判断图①、图②中两条直线是否平行,并说明方法.
图① 图②
数学活动
如图,你会过直线l外一点P画已知直线l的平行线吗?
数学活动
我们可以利用三角板和直尺画平行线:
1
2
a
b
c
1
2
c
a
b
a
b
1
2
c
当∠1与∠2相等时,直线a、b就平行了.
b
a
c
1
2
如果∠1与∠2不相等,直线a、b平行吗?
∠1与∠2是否相等,决定了直线a、b是否平行!
因此,只有当∠1=∠2时,a∥b.
1
2
3
4
5
6
8
a
b
7
c
1.∠1、∠2的边所在的直线是哪些直线
2.∠1、∠2的边所在的直线的公共直线是哪条直线
3.∠1、∠2可以看成哪两条直线被第三条直线截成的角
4.∠1、∠2在位置上有何特点
∠1、∠2都在被截两条直线的同一方向,且都在第三条直线的同旁.
获取新知
1
2
3
4
5
6
8
两条直线a、b被第三条直线c所截而成的8个角中,像∠1与∠2这样的一对角称为同位角.
∠1与∠2是由两条直线a、b被直线c所截构成的同位角.
还有其他的同位角吗?
∠3与∠4,∠5与∠6,∠7与∠8也是同位角
a
b
7
c
议一议:
同位角在数量上应具备什么样的条件,才能使对应的直线平行呢?
b
a
1
2
图中,显然a与b不平行,要使a ∥ b,必须∠1=∠2,也就是只要∠1=∠2,那么a ∥ b,而∠1与∠2是直线a、b被直线c所截而得的同位角.
基本事实:“两直线被第三条直线所截,如果同位角相等,那么这两条直线平行.”即“同位角相等,两直线平行.”
c
例题讲解
例 1 如图,∠1=∠C,∠2=∠C,请指出图中互相平行的直线,并说明理由.
A
B
C
D
1
2
解: AB∥CD,AC∥BD.
(1)因为∠1与∠C是AB、CD
被AC截成的同位角,且∠1=∠C,
所以AB∥CD.
(2)因为∠2与∠C是BD、AC
被CD截成的同位角,且∠2=∠C,
所以AC∥BD.
例 2 如图 7—1—2,根据下列条件可以判定哪两条直线互相平行,为什么
(1)∠AEB=∠D; (2) ∠EGF=∠B;
(3)∠DFG=∠A; (4) ∠EGF=∠C.
图 7-1-2
A
解∶(1)BE∥CD.理由∶因为∠AEB=∠D,根据"同位角相等,两直线平行"可得BE∥CD.
(2)CF∥AB.理由∶因为∠EGF=∠B,根据"同位角相等,两直线平行"
可得 CF∥AB.
(3)CF∥AB.理由∶因为∠DFG=∠A,根据"同位角相等,两直线平行"可得 CF∥AB.
(4)BE∥CD.理由∶因为∠EGF=∠C,根据"同位角相等,两直线平行"可得BE∥CD.
D
随堂演练
AB∥CD
同位角相等,两直线平行
1
2
b
c
a
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
