苏科版数学七年级下册同步课件:7.5 第1课时 三角形的内角和(共18张PPT)
文档属性
| 名称 | 苏科版数学七年级下册同步课件:7.5 第1课时 三角形的内角和(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 666.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第7章 平面图形的认识(二)
7.5 第1课时 三角形的内角和
问题情境
(1)小学里我们就已经知道了三角形的三个内角的和等于多少度?
(2)你有知道怎么说明三角形的三个内角的和等于180°吗?
【探究一】画图、度量、计算
请每位同学在课堂笔记本上任意画一个三角形,用量角器量出各内角的度数,并求它们的和.
数学实验
【探究二】实验操作
动画演示(见几何画板)
【探究三】拼图操作
请每位同学将课前发下的三角形纸片的3个内角(如图)剪开,然后拼在一起,观察它们的和是否为180°.
A
B
C
B
C
A
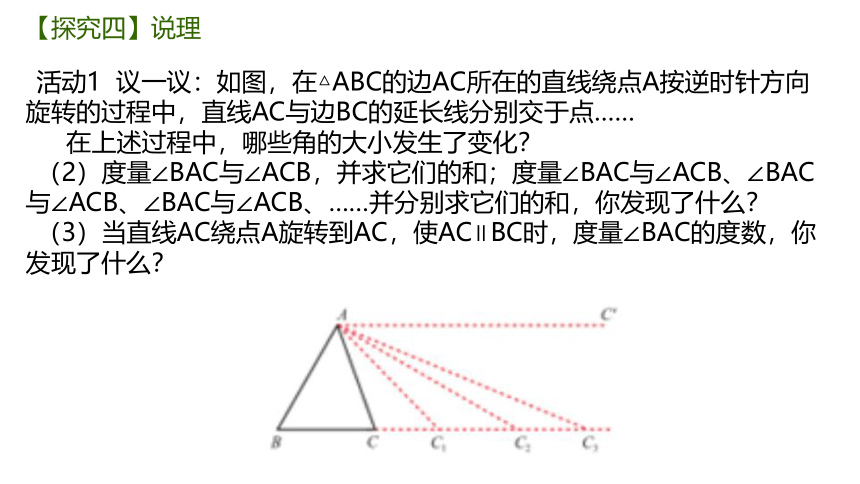
活动1 议一议:如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点……
在上述过程中,哪些角的大小发生了变化?
(2)度量∠BAC与∠ACB,并求它们的和;度量∠BAC与∠ACB、∠BAC与∠ACB、∠BAC与∠ACB、……并分别求它们的和,你发现了什么?
(3)当直线AC绕点A旋转到AC,使AC∥BC时,度量∠BAC的度数,你发现了什么?
【探究四】说理
A
a
b
B
C
⌒
⌒
1
3
c
5
⌒
4
理由:∵c//b,
∴∠5=∠4(两直线平行,内错角相等)
∴∠1+∠BAC=180°(两直线平行,同旁内角互补)
∴∠1+∠3+∠5=180°
∴∠1+∠3+∠4=180°
即△ABC的三个内角的和等于180°.
结论:三角形三个内角的和等于180°.
符号语言:
在△ABC中,∠ABC+∠ACB+∠BAC=180°
获取新知
例 1 在△ABC中,∠A=40°,∠B=∠C,求∠C的度数。
例题讲解
解:在△ABC中,
因为∠A+∠B+∠C=180°、∠A=40°,
所以∠B+∠C=180°-∠A=180°-40°=140°
因为∠B=∠C,
所以2∠C=140°,∠C=70°.
例 2 如图,△ABC的角平分线BD、CE相交于点P,∠A=70°,求∠BPC的度数。
P
解:在△ABC中,
因为∠A+∠ABC+∠ACB=180°、∠A=70°,
所以∠ABC+∠ACB=180°-∠A=180°-70°=110°
因为BD、CE分别平分∠ABC、∠ACB,
所以∠1+∠2= 1 2 ∠ABC+ 1 2 ∠ACB= 1 2 ×110°=55°
在△PBC中,
所以∠BPC=180°-(∠1+∠2)=180°-55°=125°
D
随堂演练
90
直角
65
课堂小结
回顾本节课的学习,请你回答以下几个问题:
1.三角形3个内角之间有怎样的数量关系?
2.“三角形三个内角之和等于180°”这一结论是如何探索得到的?
3.“三角形三个内角之和等于180°”这一结论在三角形有关角度计算问题上如何应用,求解问题的表达上有何要求?
第7章 平面图形的认识(二)
7.5 第1课时 三角形的内角和
问题情境
(1)小学里我们就已经知道了三角形的三个内角的和等于多少度?
(2)你有知道怎么说明三角形的三个内角的和等于180°吗?
【探究一】画图、度量、计算
请每位同学在课堂笔记本上任意画一个三角形,用量角器量出各内角的度数,并求它们的和.
数学实验
【探究二】实验操作
动画演示(见几何画板)
【探究三】拼图操作
请每位同学将课前发下的三角形纸片的3个内角(如图)剪开,然后拼在一起,观察它们的和是否为180°.
A
B
C
B
C
A
活动1 议一议:如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点……
在上述过程中,哪些角的大小发生了变化?
(2)度量∠BAC与∠ACB,并求它们的和;度量∠BAC与∠ACB、∠BAC与∠ACB、∠BAC与∠ACB、……并分别求它们的和,你发现了什么?
(3)当直线AC绕点A旋转到AC,使AC∥BC时,度量∠BAC的度数,你发现了什么?
【探究四】说理
A
a
b
B
C
⌒
⌒
1
3
c
5
⌒
4
理由:∵c//b,
∴∠5=∠4(两直线平行,内错角相等)
∴∠1+∠BAC=180°(两直线平行,同旁内角互补)
∴∠1+∠3+∠5=180°
∴∠1+∠3+∠4=180°
即△ABC的三个内角的和等于180°.
结论:三角形三个内角的和等于180°.
符号语言:
在△ABC中,∠ABC+∠ACB+∠BAC=180°
获取新知
例 1 在△ABC中,∠A=40°,∠B=∠C,求∠C的度数。
例题讲解
解:在△ABC中,
因为∠A+∠B+∠C=180°、∠A=40°,
所以∠B+∠C=180°-∠A=180°-40°=140°
因为∠B=∠C,
所以2∠C=140°,∠C=70°.
例 2 如图,△ABC的角平分线BD、CE相交于点P,∠A=70°,求∠BPC的度数。
P
解:在△ABC中,
因为∠A+∠ABC+∠ACB=180°、∠A=70°,
所以∠ABC+∠ACB=180°-∠A=180°-70°=110°
因为BD、CE分别平分∠ABC、∠ACB,
所以∠1+∠2= 1 2 ∠ABC+ 1 2 ∠ACB= 1 2 ×110°=55°
在△PBC中,
所以∠BPC=180°-(∠1+∠2)=180°-55°=125°
D
随堂演练
90
直角
65
课堂小结
回顾本节课的学习,请你回答以下几个问题:
1.三角形3个内角之间有怎样的数量关系?
2.“三角形三个内角之和等于180°”这一结论是如何探索得到的?
3.“三角形三个内角之和等于180°”这一结论在三角形有关角度计算问题上如何应用,求解问题的表达上有何要求?
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
