苏科版数学七年级下册同步课件:7.5 第2课时 多边形的内角和(共24张PPT)
文档属性
| 名称 | 苏科版数学七年级下册同步课件:7.5 第2课时 多边形的内角和(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 452.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 00:00:00 | ||
图片预览


文档简介
(共24张PPT)
第7章 平面图形的认识(二)
7.5 第2课时 多边形的内角和
问题情境
三角形的内角和等于______.
180°
任意一个四边形的内角和如何计算?
长方形的内角和等于______.
正方形的内角和等于______.
360°
360°
多边形:
在平面内,由不在同一条直线上的3条或3条以上的线段首尾依次相接组成的图形叫做多边形.
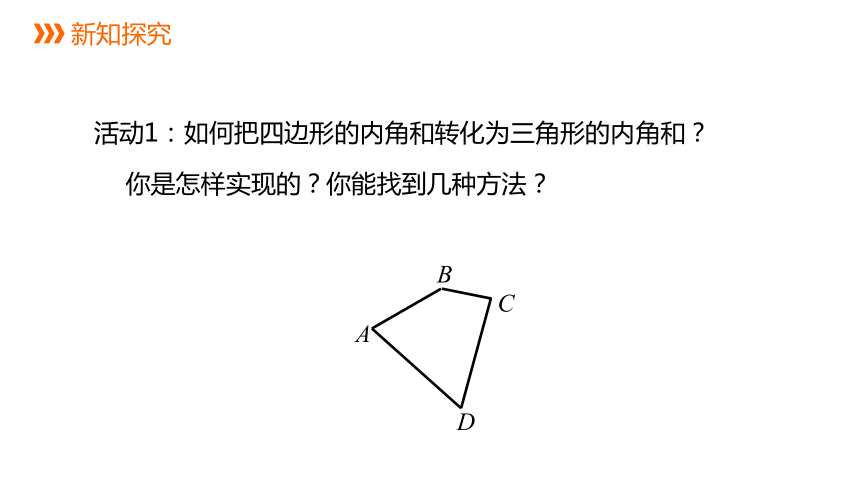
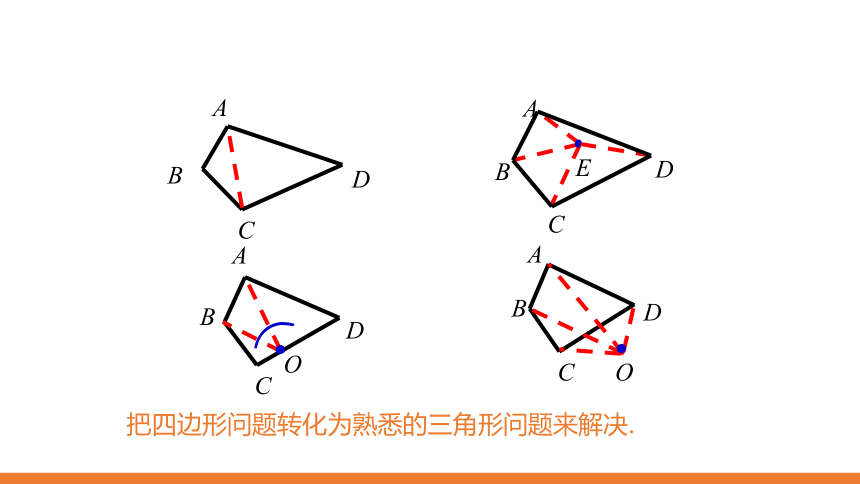
活动1:如何把四边形的内角和转化为三角形的内角和?
你是怎样实现的?你能找到几种方法?
D
C
B
A
新知探究
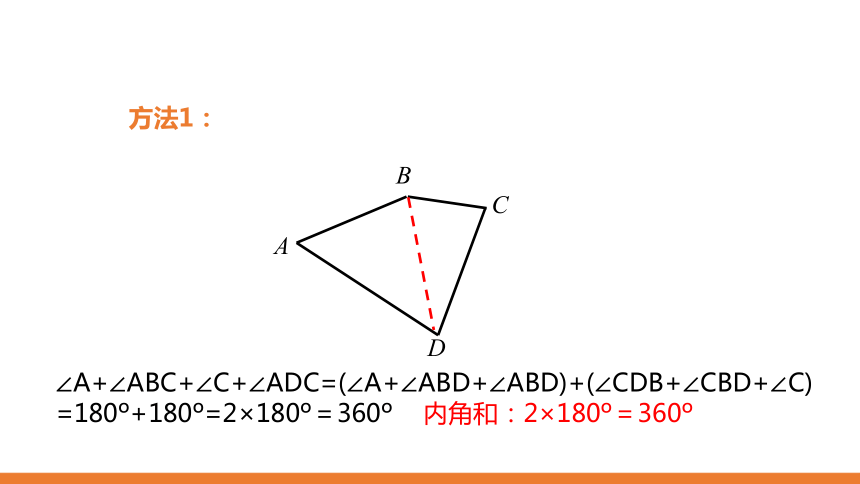
∠A+∠ABC+∠C+∠ADC=(∠A+∠ABD+∠ABD)+(∠CDB+∠CBD+∠C)=180 +180 =2×180 =360
D
C
B
A
内角和:2×180 =360
方法1:
A
C
D
B
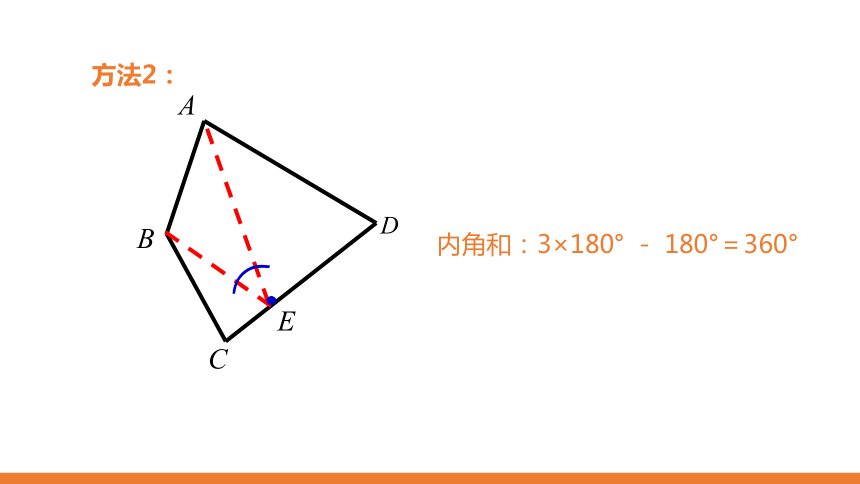
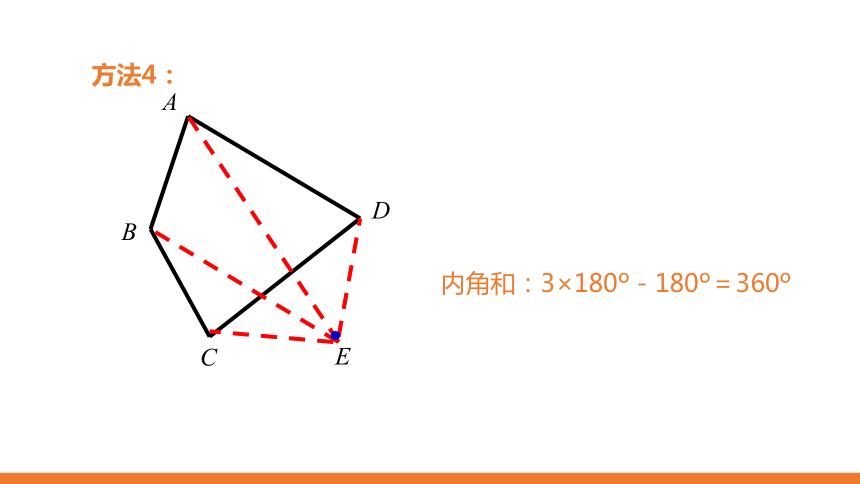
内角和:3×180° - 180°=360°
.
E
⌒
方法2:
内角和:4×180°-360 °=360 °
D
C
B
A
E
.
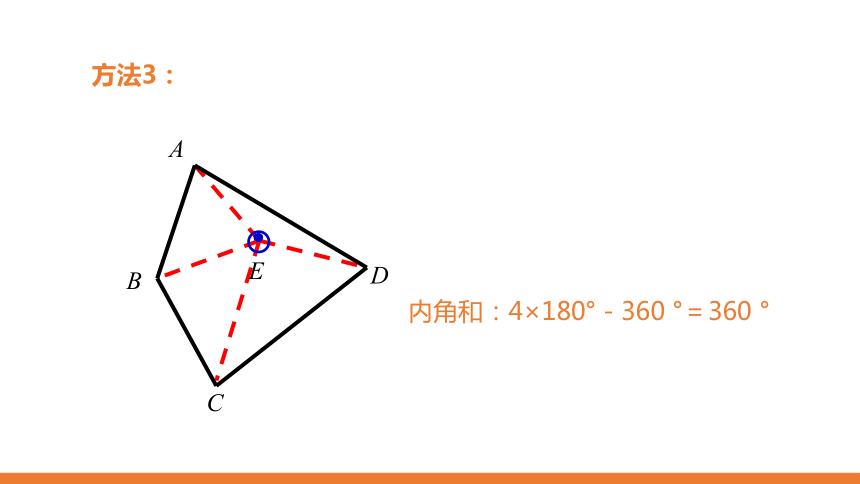
方法3:
A
C
D
B
E
内角和:3×180 -180 =360
.
方法4:
A
C
D
B
C
A
D
B
.
O
⌒
A
C
D
B
O
.
把四边形问题转化为熟悉的三角形问题来解决.
D
C
B
A
E
.
活动2 请你选择其中一种方法探索四边形的内角和.
从四边形的一个顶点出发,可以作 条对角线,它们将四边形分为 个三角形,四边形的内角和等于2个三角形内角之和。
180°×____= °.
1
2
2
360
A
B
C
D
A
B
C
D
E
如图,从五边形的一个顶点出发,可以作 条对角线,它们将五边形分为____个三角形,五边形的内角和等于3个三角形内角和。
180 × = .
2
3
3
540
活动3 探索五边形的内角和.
如图,从六边形的一个顶点出发,可以作 条对角线,它们将六边形分为 个三角形,六边形的内角和等于4个三角形内角和。
180°×___=_____°.
3
4
4
720
C
A
B
D
E
F
活动4 探索六边形的内角和.
从n 边形的一个顶点出发,可以作(n-3)条对角线,它们将n 边形分为(n-2)个三角形,这(n-2)个三角形的内角和就是n边形的内角和,所以,n边形的内角和等于(n-2)×180°.
你能从四边形、五边形、六边形的内角和的探究过程获得启发,发现多边形的内角和与边数的关系吗?
获取新知
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一个顶点引出的对角线条数
图形
边数
······
······
3-3 =0
4-3 =1
5-3 =2
6-3 =3
n-3
3-2 =1
4-2 =2
5-2 =3
6-2 =4
n-2
( n-2 )·180
180
360
540
720
······
······
······
你能从四边形、五边形、六边形的内角和的探究过程获得启发,发现多边形的内角和与边数的关系吗?
获取新知
从n 边形的一个顶点出发,可以作(n-3)条对角线,它们将n 边形分为(n-2)个三角形,这(n-2)个三角形的内角和就是n边形的内角和,所以,n边形的内角和等于(n-2)×180°.
归纳总结
例题讲解
例2 如图,在四边形ABCD中,∠A与∠C互补,∠ABC与∠ADC的平分线分别交CD、AB于点E、F,∠1与∠2有怎样的数量关系?为什么?
B
随堂演练
D
230
6
课堂小结
回顾本节课的学习,请你回答以下几个问题:
1.n边形内角和公式是什么?
2.反思n边形内角和公式的探究过程,你感悟到怎样的认知规律和什么数学思想?
第7章 平面图形的认识(二)
7.5 第2课时 多边形的内角和
问题情境
三角形的内角和等于______.
180°
任意一个四边形的内角和如何计算?
长方形的内角和等于______.
正方形的内角和等于______.
360°
360°
多边形:
在平面内,由不在同一条直线上的3条或3条以上的线段首尾依次相接组成的图形叫做多边形.
活动1:如何把四边形的内角和转化为三角形的内角和?
你是怎样实现的?你能找到几种方法?
D
C
B
A
新知探究
∠A+∠ABC+∠C+∠ADC=(∠A+∠ABD+∠ABD)+(∠CDB+∠CBD+∠C)=180 +180 =2×180 =360
D
C
B
A
内角和:2×180 =360
方法1:
A
C
D
B
内角和:3×180° - 180°=360°
.
E
⌒
方法2:
内角和:4×180°-360 °=360 °
D
C
B
A
E
.
方法3:
A
C
D
B
E
内角和:3×180 -180 =360
.
方法4:
A
C
D
B
C
A
D
B
.
O
⌒
A
C
D
B
O
.
把四边形问题转化为熟悉的三角形问题来解决.
D
C
B
A
E
.
活动2 请你选择其中一种方法探索四边形的内角和.
从四边形的一个顶点出发,可以作 条对角线,它们将四边形分为 个三角形,四边形的内角和等于2个三角形内角之和。
180°×____= °.
1
2
2
360
A
B
C
D
A
B
C
D
E
如图,从五边形的一个顶点出发,可以作 条对角线,它们将五边形分为____个三角形,五边形的内角和等于3个三角形内角和。
180 × = .
2
3
3
540
活动3 探索五边形的内角和.
如图,从六边形的一个顶点出发,可以作 条对角线,它们将六边形分为 个三角形,六边形的内角和等于4个三角形内角和。
180°×___=_____°.
3
4
4
720
C
A
B
D
E
F
活动4 探索六边形的内角和.
从n 边形的一个顶点出发,可以作(n-3)条对角线,它们将n 边形分为(n-2)个三角形,这(n-2)个三角形的内角和就是n边形的内角和,所以,n边形的内角和等于(n-2)×180°.
你能从四边形、五边形、六边形的内角和的探究过程获得启发,发现多边形的内角和与边数的关系吗?
获取新知
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一个顶点引出的对角线条数
图形
边数
······
······
3-3 =0
4-3 =1
5-3 =2
6-3 =3
n-3
3-2 =1
4-2 =2
5-2 =3
6-2 =4
n-2
( n-2 )·180
180
360
540
720
······
······
······
你能从四边形、五边形、六边形的内角和的探究过程获得启发,发现多边形的内角和与边数的关系吗?
获取新知
从n 边形的一个顶点出发,可以作(n-3)条对角线,它们将n 边形分为(n-2)个三角形,这(n-2)个三角形的内角和就是n边形的内角和,所以,n边形的内角和等于(n-2)×180°.
归纳总结
例题讲解
例2 如图,在四边形ABCD中,∠A与∠C互补,∠ABC与∠ADC的平分线分别交CD、AB于点E、F,∠1与∠2有怎样的数量关系?为什么?
B
随堂演练
D
230
6
课堂小结
回顾本节课的学习,请你回答以下几个问题:
1.n边形内角和公式是什么?
2.反思n边形内角和公式的探究过程,你感悟到怎样的认知规律和什么数学思想?
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
