苏科版数学七年级下册同步课件:7.5 第3课时 多边形的外角和(共18张PPT)
文档属性
| 名称 | 苏科版数学七年级下册同步课件:7.5 第3课时 多边形的外角和(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 434.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 00:00:00 | ||
图片预览


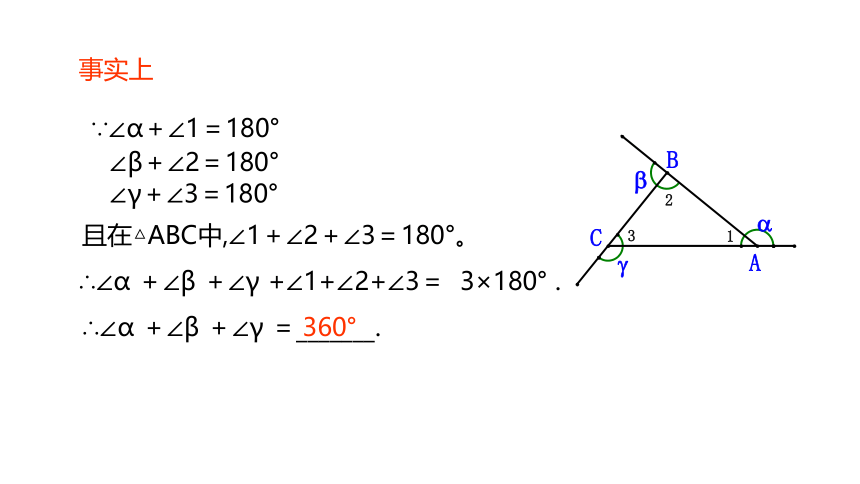

文档简介
(共18张PPT)
第7章 平面图形的认识(二)
7.5 第3课时 多边形的外角和
1.三角形的内角和
2.n边形的内角和
复习回顾
n边形的内角和等于(n-2)×180°.
三角形的内角和等于180°.
化归思想(分割成三角形)
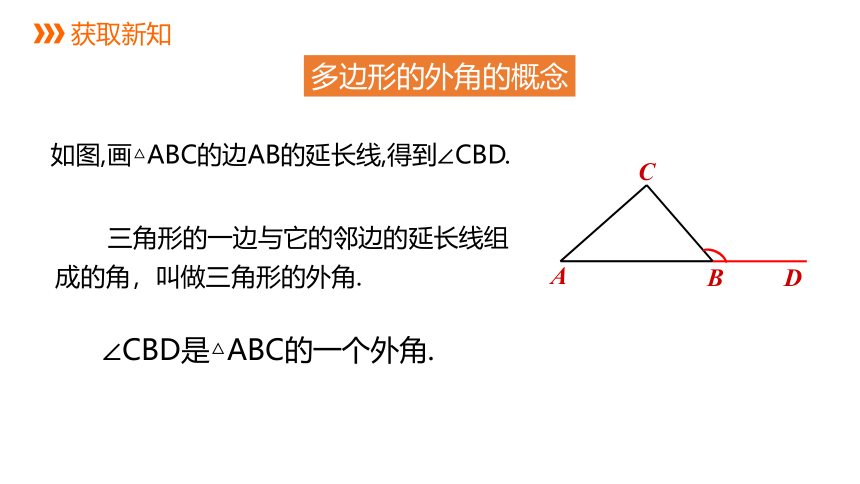
三角形的一边与它的邻边的延长线组
成的角,叫做三角形的外角.
A
B
C
如图,画△ABC的边AB的延长线,得到∠CBD.
D
)
∠CBD是△ABC的一个外角.
获取新知
多边形的外角的概念
F
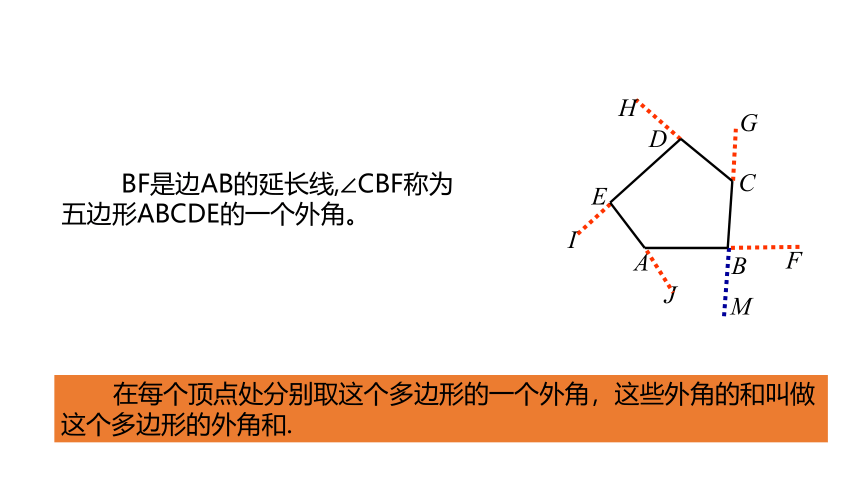
BF是边AB的延长线,∠CBF称为五边形ABCDE的一个外角。
在每个顶点处分别取这个多边形的一个外角,这些外角的和叫做这个多边形的外角和.
M
G
H
I
J
E
D
C
B
A
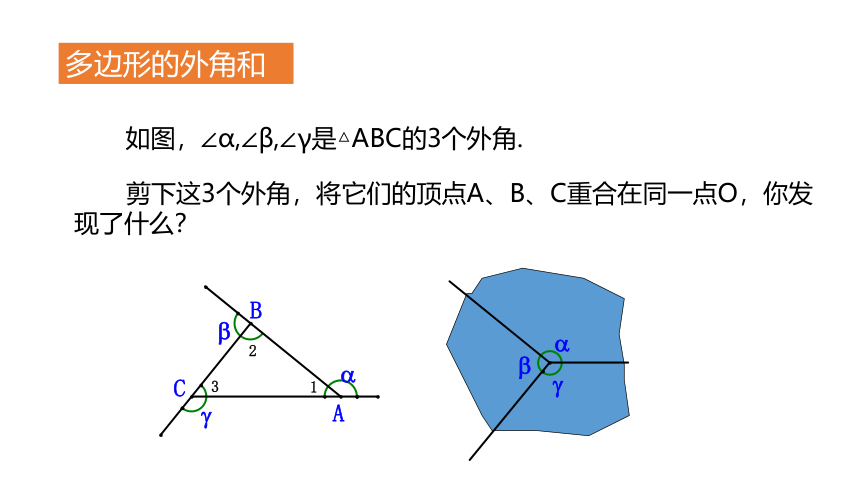
如图,∠α,∠β,∠γ是△ABC的3个外角.
剪下这3个外角,将它们的顶点A、B、C重合在同一点O,你发现了什么?
多边形的外角和
事实上
∵∠α+∠1=180°
∠β+∠2=180°
∠γ+∠3=180°
且在△ABC中,∠1+∠2+∠3=180°。
∴∠α +∠β +∠γ =_______.
360°
∴∠α +∠β +∠γ +∠1+∠2+∠3= 3×180° .
如图,∠1,∠2,∠3, ∠4是四边形ABCD的4个外角,外角和是多少?
延伸
五边形,六边形的外角和呢?
n边形的外角和呢?
事实上
∵∠BAD+∠1=180°
∠ABC+∠2=180°
∠BCD+∠3=180°
且在四边形ABCD中,
∠BAD+∠ABC+∠BCD+ ∠CDA = 2×180°,
360°
∴∠1+∠2+∠3 +∠4 = .
∠CDA+∠4=180°
任意n边形的外角和等于360°
注意:多边形的外角和与边数无关。
归纳总结
从五边形ABCDE纸片中剪去一个三角形,剩余的部分是几边形?它们的内角和、外角和分别是多少?
内角和是360°,
外角和是360°
内角和是540°,
外角和是360°
内角和是720°,
外角和是360°
△BDC
△ADO,△OCE
∠AEB
例题讲解
360
360
随堂演练
D
课堂小结
回顾本节课的学习,请你回答以下几个问题:
1.多边形外角和公式是什么?
2.反思多边形外角和公式的探究过程,你感悟到怎样的认知规律和什么数学思想?
第7章 平面图形的认识(二)
7.5 第3课时 多边形的外角和
1.三角形的内角和
2.n边形的内角和
复习回顾
n边形的内角和等于(n-2)×180°.
三角形的内角和等于180°.
化归思想(分割成三角形)
三角形的一边与它的邻边的延长线组
成的角,叫做三角形的外角.
A
B
C
如图,画△ABC的边AB的延长线,得到∠CBD.
D
)
∠CBD是△ABC的一个外角.
获取新知
多边形的外角的概念
F
BF是边AB的延长线,∠CBF称为五边形ABCDE的一个外角。
在每个顶点处分别取这个多边形的一个外角,这些外角的和叫做这个多边形的外角和.
M
G
H
I
J
E
D
C
B
A
如图,∠α,∠β,∠γ是△ABC的3个外角.
剪下这3个外角,将它们的顶点A、B、C重合在同一点O,你发现了什么?
多边形的外角和
事实上
∵∠α+∠1=180°
∠β+∠2=180°
∠γ+∠3=180°
且在△ABC中,∠1+∠2+∠3=180°。
∴∠α +∠β +∠γ =_______.
360°
∴∠α +∠β +∠γ +∠1+∠2+∠3= 3×180° .
如图,∠1,∠2,∠3, ∠4是四边形ABCD的4个外角,外角和是多少?
延伸
五边形,六边形的外角和呢?
n边形的外角和呢?
事实上
∵∠BAD+∠1=180°
∠ABC+∠2=180°
∠BCD+∠3=180°
且在四边形ABCD中,
∠BAD+∠ABC+∠BCD+ ∠CDA = 2×180°,
360°
∴∠1+∠2+∠3 +∠4 = .
∠CDA+∠4=180°
任意n边形的外角和等于360°
注意:多边形的外角和与边数无关。
归纳总结
从五边形ABCDE纸片中剪去一个三角形,剩余的部分是几边形?它们的内角和、外角和分别是多少?
内角和是360°,
外角和是360°
内角和是540°,
外角和是360°
内角和是720°,
外角和是360°
△BDC
△ADO,△OCE
∠AEB
例题讲解
360
360
随堂演练
D
课堂小结
回顾本节课的学习,请你回答以下几个问题:
1.多边形外角和公式是什么?
2.反思多边形外角和公式的探究过程,你感悟到怎样的认知规律和什么数学思想?
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
