2.1.1不等关系与重要不等式 课件(共22张PPT)
文档属性
| 名称 | 2.1.1不等关系与重要不等式 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 15:22:14 | ||
图片预览








文档简介
(共22张PPT)
2.1 等式性质与不等式性质
=
≠ >< ≥ ≤
2.1.1不等关系与重要不等式
1:你知道各图中的标志有何作用吗 其含义是什么
答案 ①最低限速:限制行驶时速v不得低于50公里; ①v≥50
②限制质量:装载总质量G不得超过10 t; ②G≤10
③限制高度:装载高度h不得超过3.5 m; ③h≤3.5
④限制宽度:装载宽度a不得超过3 m; ④a≤3
⑤时间范围:7.5≤t≤10. ⑤7.5≤t≤10
在日常生活中,我们经常看到下列标志:
学习目标及重难点
1. 了解不等式的意义,能用不等式(组)表示实际问题中的不等关系.
2. 会用作差法比较两个代数式的大小关系.(重点)
3. 掌握并会应用重要不等式.(重难点)
不等关系及其表示
1
不等关系及其表示
1
在现实世界和日常生活中,大量存在着相等关系和不等关系,例如多与少、
大与小、长与短、高与矮、远与近、快与慢、涨与跌、轻与重、不超过和不
少于等。类似于这样的问题反映在数量关系上就是相等和不相等,相等用等
式表示不等用不等式表示。
【等式】指的是用等号“=”连接起来的式子
【不等式】指的是用不等号“≠”“>”“<”“≥”“≤”
连接起来的式子
不等关系及其表示
1
【问题1】你能用不等式或不等式组表示下列问题中的不等关系吗?
(1)某路段限速;;
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量应不少于2.5%,蛋
白质的含量应不少于2.3%;
(3)三角形两边之和大于第三边,两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
设该路段行驶的汽车速度为,则
,
设三角形三边分别为,则
设P是直线AB外任意一点,PQ是P到AB的垂
线段,C是直线AB上任意一点,则PC≥PQ
A
B
C
P
Q
实数大小的比较
2
【问题2】
2
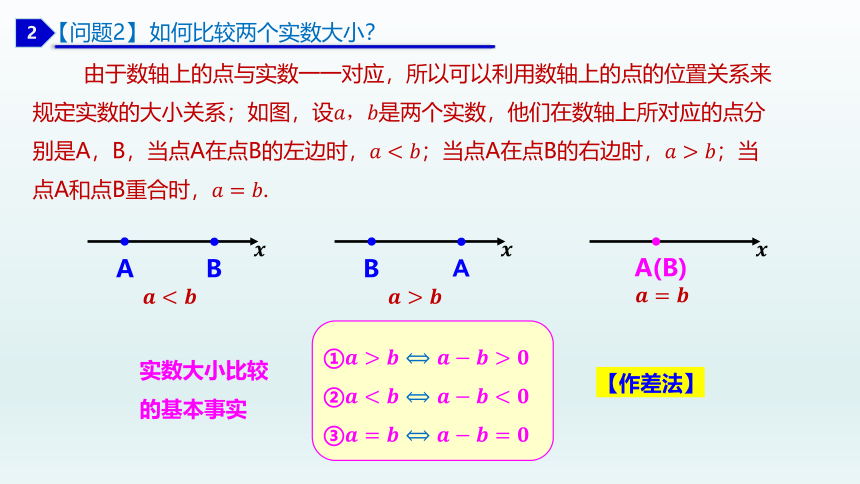
由于数轴上的点与实数一一对应,所以可以利用数轴上的点的位置关系来
规定实数的大小关系;如图,设是两个实数,他们在数轴上所对应的点分
别是A,B,当点A在点B的左边时,;当点A在点B的右边时,;当
点A和点B重合时,.
A
B
B
A
A(B)
实数大小比较
的基本事实
【作差法】
①
②
③
如何比较两个实数大小?
实数大小的比较
2
探究一:比较和的大小.
【解】运用作差法:
2>0,
>
作差
变形
定号
定论
0是相等与不等的分界线,它也为比较实数的大小提供了标杆.
实数大小的比较
2
再
【解】运用作差法:
一个重要不等式
3
若设直角三角形的两直角边分别为a,b,则
S大于S',即
A
B
C
D
E(FGH)
当a=b时,S=S',即
A
B
C
D
E
F
G
H
a
b
当a=b时
综上,
一个重要不等式
3
(1)正方形ABCD的面积S=________;
四个直角三角形的面积和S' =_____;
(2) S与S’有什么样的不等关系,如何表示?
(3)S与S’会出现相等的情况吗,什么时候相等?
【问题3】
【问题4】 :如何证明重要不等式?
证明:
重要不等式
探究二
【证】:
一个重要不等式
3
课堂训练
4
课堂训练
4
C
C
课堂训练
4
预习自测
5
预习自测
5
√
√
×
√
预习自测
5
C
2.1 等式性质与不等式性质
=
≠ >< ≥ ≤
2.1.1不等关系与重要不等式
1:你知道各图中的标志有何作用吗 其含义是什么
答案 ①最低限速:限制行驶时速v不得低于50公里; ①v≥50
②限制质量:装载总质量G不得超过10 t; ②G≤10
③限制高度:装载高度h不得超过3.5 m; ③h≤3.5
④限制宽度:装载宽度a不得超过3 m; ④a≤3
⑤时间范围:7.5≤t≤10. ⑤7.5≤t≤10
在日常生活中,我们经常看到下列标志:
学习目标及重难点
1. 了解不等式的意义,能用不等式(组)表示实际问题中的不等关系.
2. 会用作差法比较两个代数式的大小关系.(重点)
3. 掌握并会应用重要不等式.(重难点)
不等关系及其表示
1
不等关系及其表示
1
在现实世界和日常生活中,大量存在着相等关系和不等关系,例如多与少、
大与小、长与短、高与矮、远与近、快与慢、涨与跌、轻与重、不超过和不
少于等。类似于这样的问题反映在数量关系上就是相等和不相等,相等用等
式表示不等用不等式表示。
【等式】指的是用等号“=”连接起来的式子
【不等式】指的是用不等号“≠”“>”“<”“≥”“≤”
连接起来的式子
不等关系及其表示
1
【问题1】你能用不等式或不等式组表示下列问题中的不等关系吗?
(1)某路段限速;;
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量应不少于2.5%,蛋
白质的含量应不少于2.3%;
(3)三角形两边之和大于第三边,两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
设该路段行驶的汽车速度为,则
,
设三角形三边分别为,则
设P是直线AB外任意一点,PQ是P到AB的垂
线段,C是直线AB上任意一点,则PC≥PQ
A
B
C
P
Q
实数大小的比较
2
【问题2】
2
由于数轴上的点与实数一一对应,所以可以利用数轴上的点的位置关系来
规定实数的大小关系;如图,设是两个实数,他们在数轴上所对应的点分
别是A,B,当点A在点B的左边时,;当点A在点B的右边时,;当
点A和点B重合时,.
A
B
B
A
A(B)
实数大小比较
的基本事实
【作差法】
①
②
③
如何比较两个实数大小?
实数大小的比较
2
探究一:比较和的大小.
【解】运用作差法:
2>0,
>
作差
变形
定号
定论
0是相等与不等的分界线,它也为比较实数的大小提供了标杆.
实数大小的比较
2
再
【解】运用作差法:
一个重要不等式
3
若设直角三角形的两直角边分别为a,b,则
S大于S',即
A
B
C
D
E(FGH)
当a=b时,S=S',即
A
B
C
D
E
F
G
H
a
b
当a=b时
综上,
一个重要不等式
3
(1)正方形ABCD的面积S=________;
四个直角三角形的面积和S' =_____;
(2) S与S’有什么样的不等关系,如何表示?
(3)S与S’会出现相等的情况吗,什么时候相等?
【问题3】
【问题4】 :如何证明重要不等式?
证明:
重要不等式
探究二
【证】:
一个重要不等式
3
课堂训练
4
课堂训练
4
C
C
课堂训练
4
预习自测
5
预习自测
5
√
√
×
√
预习自测
5
C
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
