22.1.3.1 二次函数y=ax2+ k的图象和性质 教案
文档属性
| 名称 | 22.1.3.1 二次函数y=ax2+ k的图象和性质 教案 | 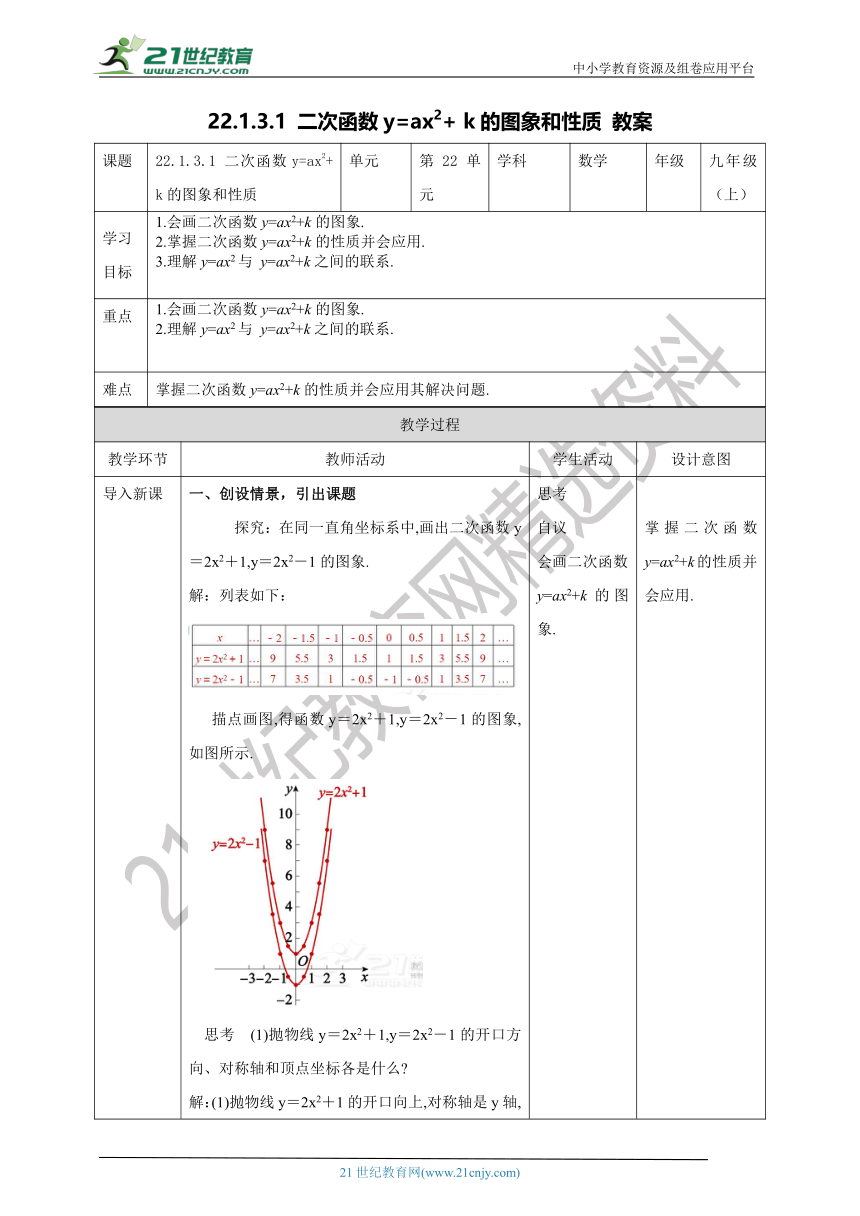 | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 16:31:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
22.1.3.1 二次函数y=ax2+ k的图象和性质 教案
课题 22.1.3.1 二次函数y=ax2+ k的图象和性质 单元 第22单元 学科 数学 年级 九年级(上)
学习目标 1.会画二次函数y=ax2+k的图象.2.掌握二次函数y=ax2+k的性质并会应用.3.理解y=ax2与 y=ax2+k之间的联系.
重点 1.会画二次函数y=ax2+k的图象.2.理解y=ax2与 y=ax2+k之间的联系.
难点 掌握二次函数y=ax2+k的性质并会应用其解决问题.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题 探究:在同一直角坐标系中,画出二次函数y=2x2+1,y=2x2-1的图象.解:列表如下: 描点画图,得函数y=2x2+1,y=2x2-1的图象,如图所示. 思考 (1)抛物线y=2x2+1,y=2x2-1的开口方向、对称轴和顶点坐标各是什么 解:(1)抛物线y=2x2+1的开口向上,对称轴是y轴,顶点坐标是(0,1);抛物线y=2x2-1的开口向上,对称轴是y轴,顶点坐标是(0,-1).(2)二次函数y=ax2+k的图象的开口方向、对称轴和顶点坐标各是什么 图象有什么特征 解:(2)二次函数y=ax2+k的图象的对称轴是y轴,顶点坐标是(0,k).当a>0时,图象开口向上,在对称轴的左侧,y随x的增大而减小,在对称轴的右侧,y随x的增大而增大,当x=0时,y有最小值;当a<0时,图象开口向下,在对称轴的左侧,y随x的增大而增大,在对称轴的右侧,y随x的增大而减小,当x=0时,y有最大值. 思考自议会画二次函数y=ax2+k的图象. 掌握二次函数y=ax2+k的性质并会应用.
讲授新课 提炼概念 二次函数y=ax2+k的图象特征与性质1.抛物线y=ax2+k的对称轴是________轴,顶点坐标是________.2.当a>0时,抛物线开口向________;在对称轴的左侧,y随x的____________,在对称轴的右侧,y随x的____________;当x=0时,y有最________值.3.当a<0时,抛物线开口向________;在对称轴的________侧,y随x的增大而增大,在对称轴的________侧,y随x的增大而减小;当x=________时,y有最大值.三、典例精讲例 (1)二次函数y=-2x2+6的图象的对称轴是________,顶点坐标是________,当x________时,y随x的增大而增大,当x________时, y有最大值,最大值是________.(2)若点A(x1,y1),B(x2,y2)都在抛物线y=-x2+3上,且x1”“=”或“<”). 解: (1) y轴,(0,6),<0,=0,6(2)< 掌握二次函数y=ax2+k的性质并会应用其解决问题. 理解y=ax2与 y=ax2+k之间的联系.
课堂检测 四、巩固训练 1. 抛物线y=2x2-3的顶点在( ) A.第一象限 B.第二象限 C.x 轴上 D. y 轴上 D2. 对于二次函数y=3x2+2,下列说法错误的是( ) A.最小值为2 B.图象与x轴没有公共点 C.当x<0时,y随x的增大而增大 D.图象的对称轴是y轴C3. 抛物线y=2x2+1是由抛物线y=2x2 ( )得到的. A.向上平移2个单位长度 B.向下平移2个单位长度 C.向上平移1个单位长度 D.向下平移1个单位长度C4.(1)抛物线 y= 2x2+3的顶点坐标是 ,对称轴是 ,在 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当 x= 时,函数y的值最大,最大值是 ,它是由抛物线 y= 2x2向 平移 个单位长度得到.(2)抛物线 y=x -5的顶点坐标是 ,对称轴是 ,在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x=____时,函数y的值最___,最小值是 . 5.已知二次函数y=3x2+k的图象上有A( 1,y1),B(2,y2),C( -3 ,y3)三点,则y1,y2,y3的大小关系是__________ .y3>y2>y1写出一个顶点坐标为(0,-3),开口方向与抛物线 y=x2的方向相反,形状相同的抛物线解析式.解:由题意可知二次函数的a=-1,并且根据顶点坐标(0,-3),可知形式为y=ax2+k的形式,且k=-3,所以符合条件的抛物线为y=-x2-3.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
22.1.3.1 二次函数y=ax2+ k的图象和性质 教案
课题 22.1.3.1 二次函数y=ax2+ k的图象和性质 单元 第22单元 学科 数学 年级 九年级(上)
学习目标 1.会画二次函数y=ax2+k的图象.2.掌握二次函数y=ax2+k的性质并会应用.3.理解y=ax2与 y=ax2+k之间的联系.
重点 1.会画二次函数y=ax2+k的图象.2.理解y=ax2与 y=ax2+k之间的联系.
难点 掌握二次函数y=ax2+k的性质并会应用其解决问题.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题 探究:在同一直角坐标系中,画出二次函数y=2x2+1,y=2x2-1的图象.解:列表如下: 描点画图,得函数y=2x2+1,y=2x2-1的图象,如图所示. 思考 (1)抛物线y=2x2+1,y=2x2-1的开口方向、对称轴和顶点坐标各是什么 解:(1)抛物线y=2x2+1的开口向上,对称轴是y轴,顶点坐标是(0,1);抛物线y=2x2-1的开口向上,对称轴是y轴,顶点坐标是(0,-1).(2)二次函数y=ax2+k的图象的开口方向、对称轴和顶点坐标各是什么 图象有什么特征 解:(2)二次函数y=ax2+k的图象的对称轴是y轴,顶点坐标是(0,k).当a>0时,图象开口向上,在对称轴的左侧,y随x的增大而减小,在对称轴的右侧,y随x的增大而增大,当x=0时,y有最小值;当a<0时,图象开口向下,在对称轴的左侧,y随x的增大而增大,在对称轴的右侧,y随x的增大而减小,当x=0时,y有最大值. 思考自议会画二次函数y=ax2+k的图象. 掌握二次函数y=ax2+k的性质并会应用.
讲授新课 提炼概念 二次函数y=ax2+k的图象特征与性质1.抛物线y=ax2+k的对称轴是________轴,顶点坐标是________.2.当a>0时,抛物线开口向________;在对称轴的左侧,y随x的____________,在对称轴的右侧,y随x的____________;当x=0时,y有最________值.3.当a<0时,抛物线开口向________;在对称轴的________侧,y随x的增大而增大,在对称轴的________侧,y随x的增大而减小;当x=________时,y有最大值.三、典例精讲例 (1)二次函数y=-2x2+6的图象的对称轴是________,顶点坐标是________,当x________时,y随x的增大而增大,当x________时, y有最大值,最大值是________.(2)若点A(x1,y1),B(x2,y2)都在抛物线y=-x2+3上,且x1
课堂检测 四、巩固训练 1. 抛物线y=2x2-3的顶点在( ) A.第一象限 B.第二象限 C.x 轴上 D. y 轴上 D2. 对于二次函数y=3x2+2,下列说法错误的是( ) A.最小值为2 B.图象与x轴没有公共点 C.当x<0时,y随x的增大而增大 D.图象的对称轴是y轴C3. 抛物线y=2x2+1是由抛物线y=2x2 ( )得到的. A.向上平移2个单位长度 B.向下平移2个单位长度 C.向上平移1个单位长度 D.向下平移1个单位长度C4.(1)抛物线 y= 2x2+3的顶点坐标是 ,对称轴是 ,在 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当 x= 时,函数y的值最大,最大值是 ,它是由抛物线 y= 2x2向 平移 个单位长度得到.(2)抛物线 y=x -5的顶点坐标是 ,对称轴是 ,在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x=____时,函数y的值最___,最小值是 . 5.已知二次函数y=3x2+k的图象上有A( 1,y1),B(2,y2),C( -3 ,y3)三点,则y1,y2,y3的大小关系是__________ .y3>y2>y1写出一个顶点坐标为(0,-3),开口方向与抛物线 y=x2的方向相反,形状相同的抛物线解析式.解:由题意可知二次函数的a=-1,并且根据顶点坐标(0,-3),可知形式为y=ax2+k的形式,且k=-3,所以符合条件的抛物线为y=-x2-3.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
