苏科版数学七年级下册同步课件:9.4 第1课时 完全平方公式(共18张PPT)
文档属性
| 名称 | 苏科版数学七年级下册同步课件:9.4 第1课时 完全平方公式(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 416.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 00:00:00 | ||
图片预览




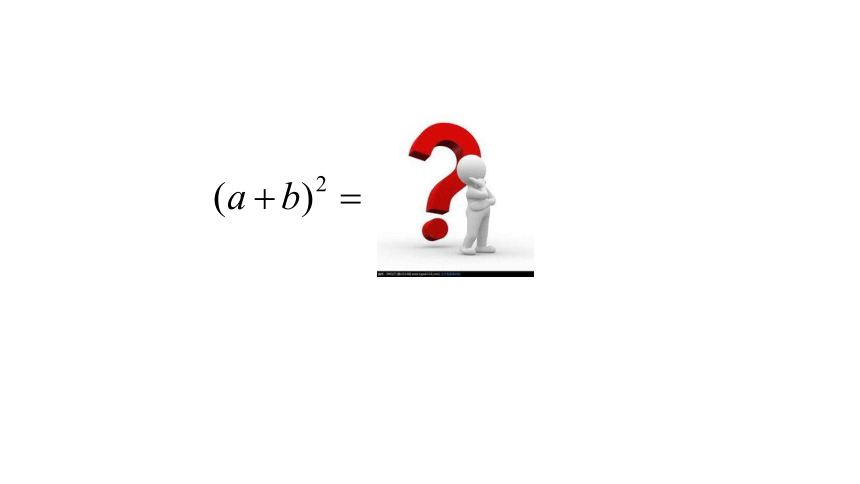

文档简介
(共18张PPT)
第9章 整式乘法与因式分解
9.4 第1课时 完全平方公式
小明认为:(a+b)2=a2+2ab+b2
小红认为:(a+b)2=a2+b2
情境引入
小红举例1:当a=0,b=0时,
(a+b)2=0;a2+b2=0.
举例2:当 a=1,b=0时,
(a+b)2=1;a2+b2=1.所以
小明举例1:当 时,
(a+b)2=0;a2+2ab+b2=0,
举例2:当 时,
(a+b)2=1;a2+2ab+b2=1,所以
a2+2ab+b2
根据多项式乘多项式法则
a2+ab+ba+b2
(a+b)2
(a+b)(a+b)
可以看作
(a+b)2=a2+2ab+b2
由多项式乘多项式可以得到:
获取新知
b
b
a
a
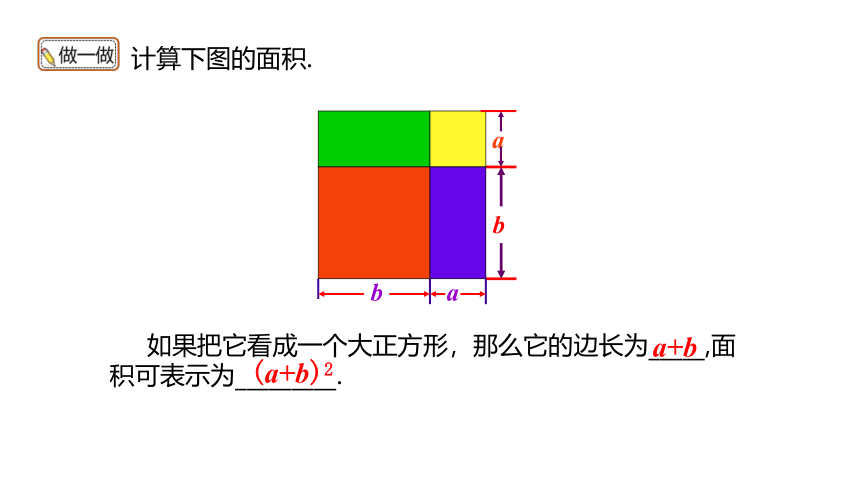
如果把它看成一个大正方形,那么它的边长为_____,面积可表示为_________.
(a+b)2
a+b
计算下图的面积.
b
b
a
a
a2+2ab+b2
(a+b)2
如果把它看成是由2个小长方形和2个小正方形组成,那么它的面积为______________.
a2+2ab+b2
利用面积的不同表示形式得到的下面的等式.
解法一:(a-b)2=(a-b)(a-b)=a2-2ab+b2
解法二:(a-b)2=[a+(-b)] 2
=a2+2.a.(-b)+(-b)2
=a2-2ab+b2
完全平方公式
你能用语言叙述完全平方公式吗?
两个数的和(差)的平方等于这两个数的平方和与它们的积的2倍的和(差).
归纳总结
特点:
(1)两个公式的左边都是一个二项式的平方,二者仅差一个“符号”不同;
(2)公式的右边都是二次三项式,其中两项是公式左边二项式中每一项的平方,简称“平方项”,中间一项是左边二项式中两项乘积的2倍,二者仅差一个“符号”不同.
首平方,尾平方,首尾2倍中间放.
(a+b)2=a2+2ab+b2
(a-b)2= a2-2ab+b2
完全平方公式
例1. 用完全平方公式计算
(1) ( 5 + 3p )2 (2) ( 2x - 7y )2 (3)(-2a-5)2
解:(1)原式=
52
+
5×3p
2×
+
(3p)2
=25+30p+9p2
例题讲解
(2)原式=(2x)2-2·2x·7y+(7y)2
=4x2-28xy+49y2
(3)原式=(-2a)2+2· (-2a)· (-5) +(-5)2
=4a2+20a+25
利用完全平方公式计算,第一步先 选择公式,明确是哪两数和(或差)的平方;第二步准确代入公式;第三步化简.
A
随堂演练
4-4x+x2
1
4. 下面的计算是否正确?如有错误,请改正:
(1) (x+y)2=x2+y2;
(2) (-m+n)2=-m2 +n2;
(3) ( a 1)2= a2 2a 1.
解: (1)
少了第一数与第二数乘积的2倍;
应改为: (x+y)2= x2+2xy+y2;
(2) 第一项平方时未加括号;(应该是(-m)2 )
少了第一数与第二数乘积的2倍 (丢了一项);
应改为: (-m+n)2= (-m)2+2 (-m)n +n2;
(3) 第一数平方未添括号,
第一数与第二数乘积的2倍 错了符号;
第二数的平方 这一项错了符号;
应改为: ( a 1)2=( a)2 2 ( a ) 1+12;
课堂小结
完全平方公式
法则
注意
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子,可能需要先添括号变形成符合公式的要求才行
3.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面)
第9章 整式乘法与因式分解
9.4 第1课时 完全平方公式
小明认为:(a+b)2=a2+2ab+b2
小红认为:(a+b)2=a2+b2
情境引入
小红举例1:当a=0,b=0时,
(a+b)2=0;a2+b2=0.
举例2:当 a=1,b=0时,
(a+b)2=1;a2+b2=1.所以
小明举例1:当 时,
(a+b)2=0;a2+2ab+b2=0,
举例2:当 时,
(a+b)2=1;a2+2ab+b2=1,所以
a2+2ab+b2
根据多项式乘多项式法则
a2+ab+ba+b2
(a+b)2
(a+b)(a+b)
可以看作
(a+b)2=a2+2ab+b2
由多项式乘多项式可以得到:
获取新知
b
b
a
a
如果把它看成一个大正方形,那么它的边长为_____,面积可表示为_________.
(a+b)2
a+b
计算下图的面积.
b
b
a
a
a2+2ab+b2
(a+b)2
如果把它看成是由2个小长方形和2个小正方形组成,那么它的面积为______________.
a2+2ab+b2
利用面积的不同表示形式得到的下面的等式.
解法一:(a-b)2=(a-b)(a-b)=a2-2ab+b2
解法二:(a-b)2=[a+(-b)] 2
=a2+2.a.(-b)+(-b)2
=a2-2ab+b2
完全平方公式
你能用语言叙述完全平方公式吗?
两个数的和(差)的平方等于这两个数的平方和与它们的积的2倍的和(差).
归纳总结
特点:
(1)两个公式的左边都是一个二项式的平方,二者仅差一个“符号”不同;
(2)公式的右边都是二次三项式,其中两项是公式左边二项式中每一项的平方,简称“平方项”,中间一项是左边二项式中两项乘积的2倍,二者仅差一个“符号”不同.
首平方,尾平方,首尾2倍中间放.
(a+b)2=a2+2ab+b2
(a-b)2= a2-2ab+b2
完全平方公式
例1. 用完全平方公式计算
(1) ( 5 + 3p )2 (2) ( 2x - 7y )2 (3)(-2a-5)2
解:(1)原式=
52
+
5×3p
2×
+
(3p)2
=25+30p+9p2
例题讲解
(2)原式=(2x)2-2·2x·7y+(7y)2
=4x2-28xy+49y2
(3)原式=(-2a)2+2· (-2a)· (-5) +(-5)2
=4a2+20a+25
利用完全平方公式计算,第一步先 选择公式,明确是哪两数和(或差)的平方;第二步准确代入公式;第三步化简.
A
随堂演练
4-4x+x2
1
4. 下面的计算是否正确?如有错误,请改正:
(1) (x+y)2=x2+y2;
(2) (-m+n)2=-m2 +n2;
(3) ( a 1)2= a2 2a 1.
解: (1)
少了第一数与第二数乘积的2倍;
应改为: (x+y)2= x2+2xy+y2;
(2) 第一项平方时未加括号;(应该是(-m)2 )
少了第一数与第二数乘积的2倍 (丢了一项);
应改为: (-m+n)2= (-m)2+2 (-m)n +n2;
(3) 第一数平方未添括号,
第一数与第二数乘积的2倍 错了符号;
第二数的平方 这一项错了符号;
应改为: ( a 1)2=( a)2 2 ( a ) 1+12;
课堂小结
完全平方公式
法则
注意
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子,可能需要先添括号变形成符合公式的要求才行
3.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
