苏科版七年级下册8.1同底数幂的乘法(共12张PPT)
文档属性
| 名称 | 苏科版七年级下册8.1同底数幂的乘法(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 226.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 00:00:00 | ||
图片预览




文档简介
(共12张PPT)
第8章 幂的运算
8.1同底数幂的乘法
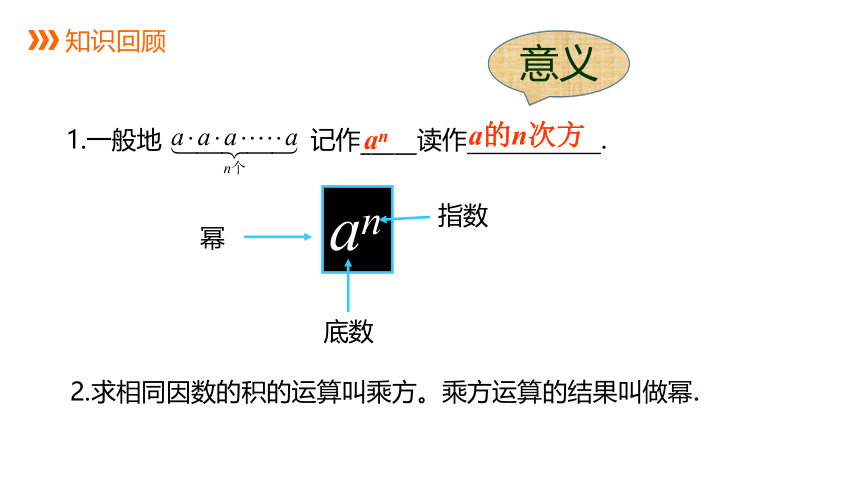
1.一般地 记作_____读作 .
知识回顾
an
幂
底数
指数
an
a的n次方
2.求相同因数的积的运算叫乘方。乘方运算的结果叫做幂.
意义
太阳光照射到地球表面所需的时间约是 5×102s,光的速度约是 3×108 m/s. 地球与太阳之间的距离约是多少
解:
( 3×108 )×( 5×102 )
情景导入
=( 3×5 )×( 108×102 )
=15×( 108×102 )
=?
108×102
=(10×10×…×10)
×(10×10)
8个10
=10×10×…×10
10个10
=1010
2个10
=1010
108×102
所以
获取新知
根据这个运算结果,可以算得地球与太阳之间地距离约为
15×1010=1.5×1011(m)
(m,n是正整数)
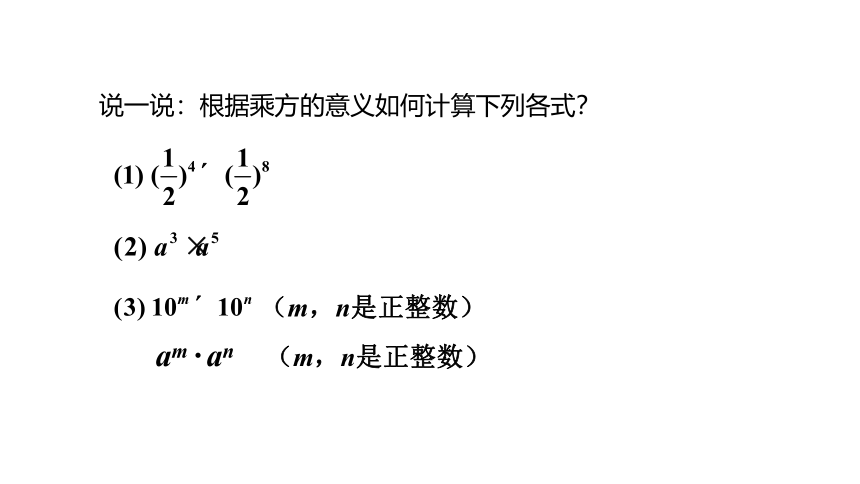
说一说:根据乘方的意义如何计算下列各式?
am · an
(m,n是正整数)
am · an =
(a · a · … · a)
m个a
对于任意的底数a,当m、n是正整数时,
n个a
= a · a · … · a
(m+n)个a
= am+n
· (a · a · … · a)
am · an = am+n (m、n都是正整数).
同底数幂相乘,
底数不变,指数相加.
同底数幂的乘法法则
归纳:am·an·ap= (m、n、p都是正整数)
am+n+p
例 1 一颗卫星绕地球运行的速度是7.9×103m/s,求这颗卫星运行1h的路程。
解:因为1 h=3.6×103 s,所以这颗卫星运行1h的路程为:
(7.9×103)×(3.6×103)
=(7.9×3.6)×(103×103)
=28.44 ×106
=2.844 ×107
答:这颗卫星运行1 h的路程为2.844 ×107 m.
2+4
x6
D
随堂演练
30
课堂小结
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数再应用法则
第8章 幂的运算
8.1同底数幂的乘法
1.一般地 记作_____读作 .
知识回顾
an
幂
底数
指数
an
a的n次方
2.求相同因数的积的运算叫乘方。乘方运算的结果叫做幂.
意义
太阳光照射到地球表面所需的时间约是 5×102s,光的速度约是 3×108 m/s. 地球与太阳之间的距离约是多少
解:
( 3×108 )×( 5×102 )
情景导入
=( 3×5 )×( 108×102 )
=15×( 108×102 )
=?
108×102
=(10×10×…×10)
×(10×10)
8个10
=10×10×…×10
10个10
=1010
2个10
=1010
108×102
所以
获取新知
根据这个运算结果,可以算得地球与太阳之间地距离约为
15×1010=1.5×1011(m)
(m,n是正整数)
说一说:根据乘方的意义如何计算下列各式?
am · an
(m,n是正整数)
am · an =
(a · a · … · a)
m个a
对于任意的底数a,当m、n是正整数时,
n个a
= a · a · … · a
(m+n)个a
= am+n
· (a · a · … · a)
am · an = am+n (m、n都是正整数).
同底数幂相乘,
底数不变,指数相加.
同底数幂的乘法法则
归纳:am·an·ap= (m、n、p都是正整数)
am+n+p
例 1 一颗卫星绕地球运行的速度是7.9×103m/s,求这颗卫星运行1h的路程。
解:因为1 h=3.6×103 s,所以这颗卫星运行1h的路程为:
(7.9×103)×(3.6×103)
=(7.9×3.6)×(103×103)
=28.44 ×106
=2.844 ×107
答:这颗卫星运行1 h的路程为2.844 ×107 m.
2+4
x6
D
随堂演练
30
课堂小结
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数再应用法则
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
