七年级下册数学人教版第六章实数全章学案(共7课时)
文档属性
| 名称 | 七年级下册数学人教版第六章实数全章学案(共7课时) |  | |
| 格式 | zip | ||
| 文件大小 | 216.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-16 09:47:27 | ||
图片预览

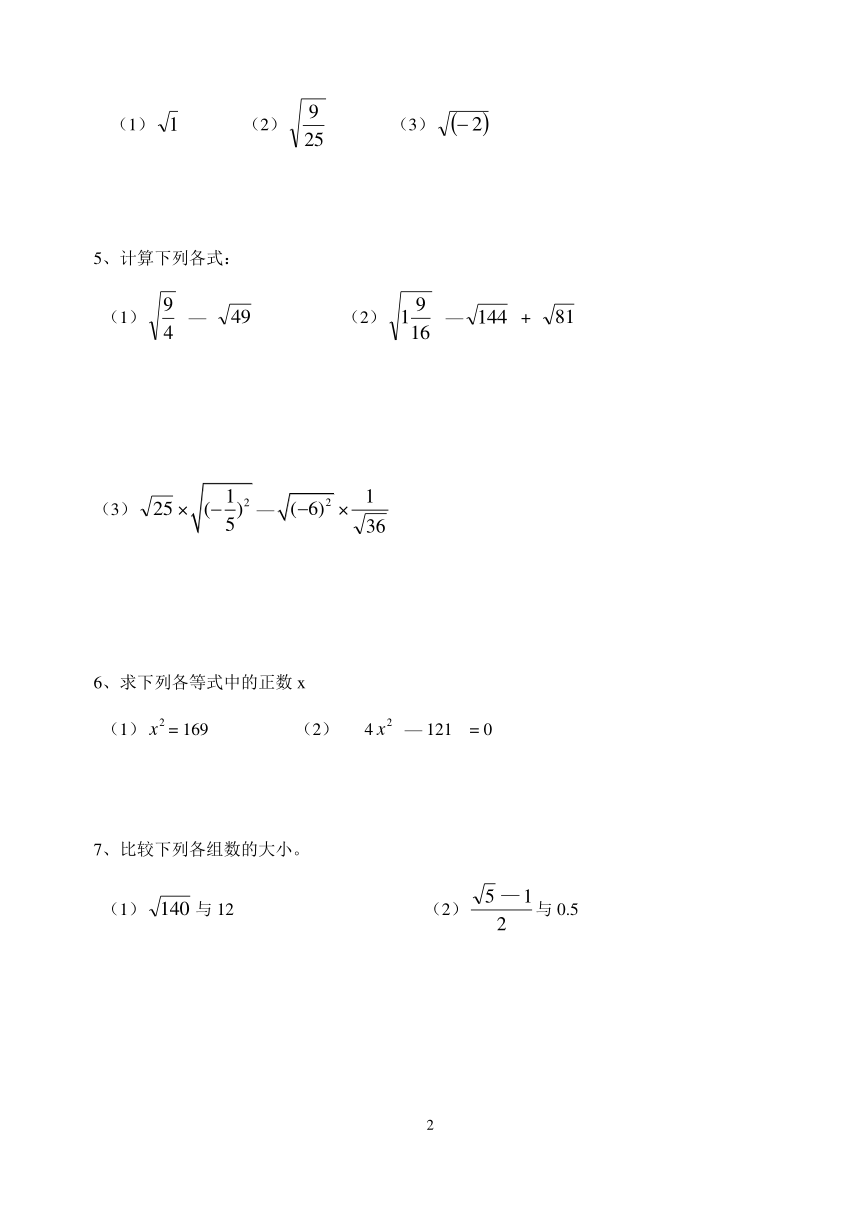



文档简介
6.1平方根(第一课时)
学习目标:
理解数的算术平方根的概念,并会用符号表示。
理解平方与开平方是互为逆运算。
会求一些非负数的算术平方根。
自学指导:
认真学习课本40—46页的内容,完成下列要求:
1、中被开方数a的范围怎样。0的算术平方根的意义。
2、完成例1,注意例1的书写格式。
3、学习例3的内容,注意与7是怎样比较的。
4、自学后完成展示内容,20分钟后进行展示。
展示内容:
1、 ∵ = ∴ 4的算术平方根是 即
∵ = ∴ 的算术平方根是 即
2、∵正数a的算术平方根是,
∴2的算术平方根是
∵4的算术平方根是2,
∴ =
3、求下列各数的算术平方根:
⑴ 0.0025 ⑵ 121 ⑶ ⑷ ⑸ 7
4、求下列各式的值:
(1) (2) (3)
5、计算下列各式:
(1) — (2) — +
(3)×—×
6、求下列各等式中的正数x
(1)= 169 (2) 4 — 121 = 0
7、比较下列各组数的大小。
(1)与12 (2)与0.5
6.1 平方根(第二课时)
学习目标
理解平方根的概念
了解开平方的定义
掌握平方根的性质
自学指导
认真阅读40-46页内容,完成下列要求:
说明:一个正数a的算术平方根有__个,平方根有__个,并且互为____,0的平方根是___。
负数有没有平方根,为什么?
注意根号前的符号
自学20分钟后,进行展示活动
展示内容
填表:
X 8 -8 -
121 0.36 0
计算下列各式的值:
(1) (2)- (3)± (4)-
平方根起源于正方形的面积,若一个正方形的面积为A,那么这个正方形的边长为多少?
判断下列说法是否正确
(1)5是25的算术平方根( )
(2)是的一个平方根( )
(3)的平方根是-4( )
(4)0的平方根与算术平方根都是0( )
5、下列各式是否有意义,为什么?
-(2)(3)(4)
6、求下列各式的x的值:
(1)=25 (2)-81=0
(3)25=36 (4)2-18=0
6.2 立方根
学习目标:1、理解并掌握立方根的概念,会用符号表示一个数的立方根。
2、会求一个数的立方根。
自学指导: 自学课本49—52页内容,完成下列要求:
1、理解立方根的概念,理解立方与开立方是互为逆运算。
2、独立完成49页探究内容,组内合作交流,归纳出正数、负数、0的立方根的特点。
3、理解与—的相等关系。
4、自学后完成展示内容,20分钟后进行展示。
展示内容:
1、如果一个数的立方根等于 ,那么这个数叫做 的 或 。
2、求一个数的 的运算,叫做 。 与
互为逆运算。
3、正数的立方根是 数,负数的立方根是 数,0的立方根是 。
4、符号中,3是 ,中的 不能省略。
5、 —
6、课本79页练习1、3、4题.
7、求下列各数的立方根:
(1)—8 (2) (3) ±125 (4) 81×9
8、求下列各式的值。
(1)— (2)— (3)
(4)(5)—
6.3实数(第一课时)
学习目标:
1、了解实数的意义,能对实数按要求进行分类。
2、了解实数范围内,相反数、倒数、绝对值的意义。
3、了解数轴上的点与实数一一对应,能用数轴上的点来表示无理数。
学习重点:理解实数的概念。
学习难点:正确理解实数的概念。
学前准备
有理数 有理数
二、探究新知
1、归纳: 任何一个有理数都可以写成_______小数或________小数的形式。反过来,任何______小数或____________小数也都是有理数
观察 通过前面的探讨和学习,我们知道,很多数的_____根和______根都是____________小数, ____________小数又叫无理数,也是无理数
结论: _______和_______统称为实数
你能举出一些无理数吗?
2、试一试 把实数分类
像有理数一样,无理数也有正负之分。例如,,是____无理数,,,是____无理数。由于非0有理数和无理数都有正负之分,所以实数也可以这样分类:
实数
3、我们知道,每个有理数都可以用数轴上的点来表示。无理数是否也可以用数轴上的点来表示呢?
(1)如图所示,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O′,点O′的坐标是多少?
从图中可以看出OO′的长时这个圆的周长______,点O′的坐标是_______
这样,无理数可以用数轴上的点表示出来
(2)
总结 ①事实上,每一个无理数都可以用数轴上的__________表示出来,这就是说,数轴上的点有些表示__________,有些表示__________
当从有理数扩充到实数以后,实数与数轴上的点就是__________的,即每一个实数都可以用数轴上的__________来表示;反过来,数轴上的__________都是表示一个实数
与有理数一样,对于数轴上的任意两个点,右边的点所表示的实数总比左边的点表示的实数______
4、讨论 当数从有理数扩充到实数以后,有理数关于相反数和绝对值的意义同样适合于实数吗?
总结 数的相反数是______,这里表示任意____________。一个正实数的绝对值是______;一个负实数的绝对值是它的______;0的绝对值是______
学以致用
例1、把下列各数分别填入相应的集合里:
正有理数{ }
负有理数{ }
正无理数{ }
负无理数{ }
2、下列实数中是无理数的为( )A. 0 B. C. D.
3、 的相反数是 ,绝对值
4、绝对值等于 的数是 , 的平方是
5、
6、求绝对值
练习:
一、判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。 ( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
二、填空1、
2、
3、比较大小
4、_________
四、总结反思 这节课你有什么新发现?知道了哪些新知识?
无理数的特征:
1.圆周率及一些含有的数
2.开不尽方的数
3.有一定的规律,但循环的无限小数
注意:带根号的数不一定是无理数
五、自我测试
1、 把下列各数填入相应的集合内:
有理数集合{ } 无理数集合{ }
整数集合{ } 分数集合{ }
实数集合{ }
2、下列各数中,是无理数的是( )A. B. C. D.
3、已知四个命题,正确的有( )
⑴有理数与无理数之和是无理数 ⑵有理数与无理数之积是无理数
⑶无理数与无理数之积是无理数 ⑷无理数与无理数之积是无理数
A. 1个 B. 2个 C. 3个 D.4个
4、若实数满足,则( )
A. B. C. D.
5、下列说法正确的有( )
⑴不存在绝对值最小的无理数 ⑵不存在绝对值最小的实数
⑶不存在与本身的算术平方根相等的数 ⑷比正实数小的数都是负实数
⑸非负实数中最小的数是0
A. 2个 B. 3个 C. 4个 D.5个
6、⑴的相反数是_________ ,绝对值是_________
⑵ ⑶若,则 _________
⑷_______7、是实数,则_____
6.3实数(第二课时)
了解实数的运算法则及运算律,会进行实数的运算
明确有理数与实数的对比
自学指导
自学课本84-96页内容
回顾复习有理数的绝对值
小组交流课本84戊思考题,归纳实数的相反数和绝对值的结果
明白有理数的运算法则及运算性质在进行实数的运算中,同样适用
展示内容
写出下列各数的相反数:
(1)- (2) -3.14 (3)一
2、||=___;若|a|=,则a=___.
3、计算下列各式的值:
(1)(+)-
(2)3+2
(3)(-)-2(-)
课本86页1、2、3、4
课题:实数复习(第一课时)
一、知识结构
乘方开方
二、知识回顾
算术平方根的定义:
平方根的定义:
平方根的性质:
立方根的定义:
立方根的性质:
练习:1、—8是 的平方根; 64的平方根是 ; ;
—64的立方根是 ; ; 的平方根是 。
2、大于而小于的所有整数为
几个基本公式:(注意字母的取值范围)
= ; = = ; = ; =
练习:;
无理数的定义:
实数的定义:
实数与 上的点是一一对应的
练习:1、判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。 ( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。 ( )
7.平面直角坐标系中的点与有序实数对之间是一一对应的。( )
2、把下列各数中,有理数为 ;无理数为
(相邻两个3之间的7逐渐加1个)
三、知识巩固1、取何值时,下列各式有意义
(1) : ;(2): ;(3):
2、
四、知识提高
1、已知,,(1) ;(2) ;
(3)0.03的平方根约为 ;(4)若,则
练习:已知,,,求(1) ;
(2)3000的立方根约为 ;(3),则
2、若,则的取值范围是
3、已知位置如图所示,
试化简 :(1) (2)
4、已知的小数部分为,的小数部分为,则
五、当堂反馈
1、下列说法正确的是( )
A、的平方根是 B、表示6的算术平方根的相反数
C、 任何数都有平方根 D、一定没有平方根
2、若,则
3、若,则的取值范围是 ;,则的取值范围是
4、已知,求的平方根
5、已知等腰三角形的两边长满足,求三角形的周长
6、如果一个数的平方根是和,求这个数
(选作)1、若为实数,则下列命题正确的是( )
A、 B、
C、 D、
2、已知,求的值。
课题:实数复习(第二课时)
一.典例分析
【 例1 】把下列各数填入相应的集合中(只填序号):
①3.14 ② ③ ④ ⑤0 ⑥ ⑦ ⑧0.15
有理数集合:{ …}正数集合{ …}
无理数集合:{ …}负数集合{ …}
分数集合:{ …}
【 例2 】计算:(1) (2)
二、检测:
1.25的平方根是( )
A、5 B、-5 C、±5 D、
2.下列说法错误的是 ( )
A、无理数的相反数还是无理数 B、无限小数都是无理数
C、正数、负数统称有理数 D、实数与数轴上的点一一对应
3.下列各组数中互为相反数的是( )
A、 -2与 B、 -2与 C、 -2与 D、与2
4.在下列各数:、、、、、、中,无理数的个数是 ( )A、2 B、3 C、4 D、5
5.满足的整数是( )
A、 B、 C、 D、
6.当的值为最小值时, 的取值为( )
A、-1 B、0 C、 D、1
7.如图,线段、,那么,线段EF的长度为( )
A、 B、 C、 D、
8.的平方根是, 64的立方根是,则的值为( )
A、3 B、7 C、3或7 D、1或7
9.平方根等于本身的实数是 。
10.化简: 。
11.的平方根是 ;的算术平方根是 ;125的立方根是 。
12.估计的大小约等于 或 (误差小于1)。
13.若,则= 。
14.比较下列实数的大小(在 填上 > 、< 或 =)
① ; ② ; ③ 。
15.计算(1) (2)
16.若x、y都是实数,且y= 求x+y的值。
PAGE
14
学习目标:
理解数的算术平方根的概念,并会用符号表示。
理解平方与开平方是互为逆运算。
会求一些非负数的算术平方根。
自学指导:
认真学习课本40—46页的内容,完成下列要求:
1、中被开方数a的范围怎样。0的算术平方根的意义。
2、完成例1,注意例1的书写格式。
3、学习例3的内容,注意与7是怎样比较的。
4、自学后完成展示内容,20分钟后进行展示。
展示内容:
1、 ∵ = ∴ 4的算术平方根是 即
∵ = ∴ 的算术平方根是 即
2、∵正数a的算术平方根是,
∴2的算术平方根是
∵4的算术平方根是2,
∴ =
3、求下列各数的算术平方根:
⑴ 0.0025 ⑵ 121 ⑶ ⑷ ⑸ 7
4、求下列各式的值:
(1) (2) (3)
5、计算下列各式:
(1) — (2) — +
(3)×—×
6、求下列各等式中的正数x
(1)= 169 (2) 4 — 121 = 0
7、比较下列各组数的大小。
(1)与12 (2)与0.5
6.1 平方根(第二课时)
学习目标
理解平方根的概念
了解开平方的定义
掌握平方根的性质
自学指导
认真阅读40-46页内容,完成下列要求:
说明:一个正数a的算术平方根有__个,平方根有__个,并且互为____,0的平方根是___。
负数有没有平方根,为什么?
注意根号前的符号
自学20分钟后,进行展示活动
展示内容
填表:
X 8 -8 -
121 0.36 0
计算下列各式的值:
(1) (2)- (3)± (4)-
平方根起源于正方形的面积,若一个正方形的面积为A,那么这个正方形的边长为多少?
判断下列说法是否正确
(1)5是25的算术平方根( )
(2)是的一个平方根( )
(3)的平方根是-4( )
(4)0的平方根与算术平方根都是0( )
5、下列各式是否有意义,为什么?
-(2)(3)(4)
6、求下列各式的x的值:
(1)=25 (2)-81=0
(3)25=36 (4)2-18=0
6.2 立方根
学习目标:1、理解并掌握立方根的概念,会用符号表示一个数的立方根。
2、会求一个数的立方根。
自学指导: 自学课本49—52页内容,完成下列要求:
1、理解立方根的概念,理解立方与开立方是互为逆运算。
2、独立完成49页探究内容,组内合作交流,归纳出正数、负数、0的立方根的特点。
3、理解与—的相等关系。
4、自学后完成展示内容,20分钟后进行展示。
展示内容:
1、如果一个数的立方根等于 ,那么这个数叫做 的 或 。
2、求一个数的 的运算,叫做 。 与
互为逆运算。
3、正数的立方根是 数,负数的立方根是 数,0的立方根是 。
4、符号中,3是 ,中的 不能省略。
5、 —
6、课本79页练习1、3、4题.
7、求下列各数的立方根:
(1)—8 (2) (3) ±125 (4) 81×9
8、求下列各式的值。
(1)— (2)— (3)
(4)(5)—
6.3实数(第一课时)
学习目标:
1、了解实数的意义,能对实数按要求进行分类。
2、了解实数范围内,相反数、倒数、绝对值的意义。
3、了解数轴上的点与实数一一对应,能用数轴上的点来表示无理数。
学习重点:理解实数的概念。
学习难点:正确理解实数的概念。
学前准备
有理数 有理数
二、探究新知
1、归纳: 任何一个有理数都可以写成_______小数或________小数的形式。反过来,任何______小数或____________小数也都是有理数
观察 通过前面的探讨和学习,我们知道,很多数的_____根和______根都是____________小数, ____________小数又叫无理数,也是无理数
结论: _______和_______统称为实数
你能举出一些无理数吗?
2、试一试 把实数分类
像有理数一样,无理数也有正负之分。例如,,是____无理数,,,是____无理数。由于非0有理数和无理数都有正负之分,所以实数也可以这样分类:
实数
3、我们知道,每个有理数都可以用数轴上的点来表示。无理数是否也可以用数轴上的点来表示呢?
(1)如图所示,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O′,点O′的坐标是多少?
从图中可以看出OO′的长时这个圆的周长______,点O′的坐标是_______
这样,无理数可以用数轴上的点表示出来
(2)
总结 ①事实上,每一个无理数都可以用数轴上的__________表示出来,这就是说,数轴上的点有些表示__________,有些表示__________
当从有理数扩充到实数以后,实数与数轴上的点就是__________的,即每一个实数都可以用数轴上的__________来表示;反过来,数轴上的__________都是表示一个实数
与有理数一样,对于数轴上的任意两个点,右边的点所表示的实数总比左边的点表示的实数______
4、讨论 当数从有理数扩充到实数以后,有理数关于相反数和绝对值的意义同样适合于实数吗?
总结 数的相反数是______,这里表示任意____________。一个正实数的绝对值是______;一个负实数的绝对值是它的______;0的绝对值是______
学以致用
例1、把下列各数分别填入相应的集合里:
正有理数{ }
负有理数{ }
正无理数{ }
负无理数{ }
2、下列实数中是无理数的为( )A. 0 B. C. D.
3、 的相反数是 ,绝对值
4、绝对值等于 的数是 , 的平方是
5、
6、求绝对值
练习:
一、判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。 ( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
二、填空1、
2、
3、比较大小
4、_________
四、总结反思 这节课你有什么新发现?知道了哪些新知识?
无理数的特征:
1.圆周率及一些含有的数
2.开不尽方的数
3.有一定的规律,但循环的无限小数
注意:带根号的数不一定是无理数
五、自我测试
1、 把下列各数填入相应的集合内:
有理数集合{ } 无理数集合{ }
整数集合{ } 分数集合{ }
实数集合{ }
2、下列各数中,是无理数的是( )A. B. C. D.
3、已知四个命题,正确的有( )
⑴有理数与无理数之和是无理数 ⑵有理数与无理数之积是无理数
⑶无理数与无理数之积是无理数 ⑷无理数与无理数之积是无理数
A. 1个 B. 2个 C. 3个 D.4个
4、若实数满足,则( )
A. B. C. D.
5、下列说法正确的有( )
⑴不存在绝对值最小的无理数 ⑵不存在绝对值最小的实数
⑶不存在与本身的算术平方根相等的数 ⑷比正实数小的数都是负实数
⑸非负实数中最小的数是0
A. 2个 B. 3个 C. 4个 D.5个
6、⑴的相反数是_________ ,绝对值是_________
⑵ ⑶若,则 _________
⑷_______7、是实数,则_____
6.3实数(第二课时)
了解实数的运算法则及运算律,会进行实数的运算
明确有理数与实数的对比
自学指导
自学课本84-96页内容
回顾复习有理数的绝对值
小组交流课本84戊思考题,归纳实数的相反数和绝对值的结果
明白有理数的运算法则及运算性质在进行实数的运算中,同样适用
展示内容
写出下列各数的相反数:
(1)- (2) -3.14 (3)一
2、||=___;若|a|=,则a=___.
3、计算下列各式的值:
(1)(+)-
(2)3+2
(3)(-)-2(-)
课本86页1、2、3、4
课题:实数复习(第一课时)
一、知识结构
乘方开方
二、知识回顾
算术平方根的定义:
平方根的定义:
平方根的性质:
立方根的定义:
立方根的性质:
练习:1、—8是 的平方根; 64的平方根是 ; ;
—64的立方根是 ; ; 的平方根是 。
2、大于而小于的所有整数为
几个基本公式:(注意字母的取值范围)
= ; = = ; = ; =
练习:;
无理数的定义:
实数的定义:
实数与 上的点是一一对应的
练习:1、判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。 ( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。 ( )
7.平面直角坐标系中的点与有序实数对之间是一一对应的。( )
2、把下列各数中,有理数为 ;无理数为
(相邻两个3之间的7逐渐加1个)
三、知识巩固1、取何值时,下列各式有意义
(1) : ;(2): ;(3):
2、
四、知识提高
1、已知,,(1) ;(2) ;
(3)0.03的平方根约为 ;(4)若,则
练习:已知,,,求(1) ;
(2)3000的立方根约为 ;(3),则
2、若,则的取值范围是
3、已知位置如图所示,
试化简 :(1) (2)
4、已知的小数部分为,的小数部分为,则
五、当堂反馈
1、下列说法正确的是( )
A、的平方根是 B、表示6的算术平方根的相反数
C、 任何数都有平方根 D、一定没有平方根
2、若,则
3、若,则的取值范围是 ;,则的取值范围是
4、已知,求的平方根
5、已知等腰三角形的两边长满足,求三角形的周长
6、如果一个数的平方根是和,求这个数
(选作)1、若为实数,则下列命题正确的是( )
A、 B、
C、 D、
2、已知,求的值。
课题:实数复习(第二课时)
一.典例分析
【 例1 】把下列各数填入相应的集合中(只填序号):
①3.14 ② ③ ④ ⑤0 ⑥ ⑦ ⑧0.15
有理数集合:{ …}正数集合{ …}
无理数集合:{ …}负数集合{ …}
分数集合:{ …}
【 例2 】计算:(1) (2)
二、检测:
1.25的平方根是( )
A、5 B、-5 C、±5 D、
2.下列说法错误的是 ( )
A、无理数的相反数还是无理数 B、无限小数都是无理数
C、正数、负数统称有理数 D、实数与数轴上的点一一对应
3.下列各组数中互为相反数的是( )
A、 -2与 B、 -2与 C、 -2与 D、与2
4.在下列各数:、、、、、、中,无理数的个数是 ( )A、2 B、3 C、4 D、5
5.满足的整数是( )
A、 B、 C、 D、
6.当的值为最小值时, 的取值为( )
A、-1 B、0 C、 D、1
7.如图,线段、,那么,线段EF的长度为( )
A、 B、 C、 D、
8.的平方根是, 64的立方根是,则的值为( )
A、3 B、7 C、3或7 D、1或7
9.平方根等于本身的实数是 。
10.化简: 。
11.的平方根是 ;的算术平方根是 ;125的立方根是 。
12.估计的大小约等于 或 (误差小于1)。
13.若,则= 。
14.比较下列实数的大小(在 填上 > 、< 或 =)
① ; ② ; ③ 。
15.计算(1) (2)
16.若x、y都是实数,且y= 求x+y的值。
PAGE
14
