6.2.1 频率的稳定性(1) 课件(共23张PPT)
文档属性
| 名称 | 6.2.1 频率的稳定性(1) 课件(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 21:29:02 | ||
图片预览






文档简介
(共23张PPT)
6.2.1频率的稳定性(1)
第六章
概率初步
七年级数学下册同步(北师大版)
学习目标
1.通过试验让学生理解当试验次数较大时,实验的频率具有稳定性,并据此能初步估计出某一事件发生的可能性大小。
2.大量重复试验得到频率的稳定值的分析。
导入新课
在一定条件下可能发生也可能不发生的事件,叫做随机事件,也称为为不确定事件。
注意:不可能事件是属于确定事件而不属于不确定事件。
1.什么是必然事件?
在一定条件下一定会发生的事件,称为必然事件
2.什么是不可能事件?
在一定条件下一定不会发生的事件称为不可能事件
3.什么是确定的事件?
必然事件与不可能事件统称为确定的事件
4.什么是不确定事件?
导入新课
周末,小明和小军在家制作照片墙,但是图钉不够用,派谁去买呢?于是小明提出掷图钉的建议:掷一枚图钉,落地后会出现两种情况,如果钉尖朝上,小军去;如果钉尖朝下,小明去.
直觉告诉我,任意掷一枚图钉,钉尖朝上和钉尖朝下的可能性是不相同的.
其实我的直觉和你一样,但我不知道对不对.
讲授新课
频率的稳定性
你认为钉尖朝上和钉尖朝下的可能性一样大吗?
不确定,要看图钉的材质
可能一样吧~
钉尖朝上的可能性大,图钉钉帽看起来比较重,更容易与地面接触
不妨让我们用试验来验证吧!
讲授新课
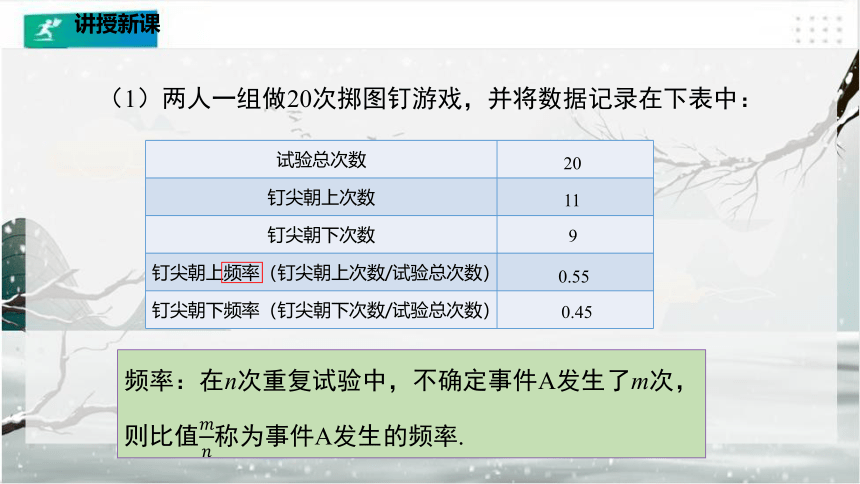
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
试验总次数
钉尖朝上次数
钉尖朝下次数
钉尖朝上频率(钉尖朝上次数/试验总次数)
钉尖朝下频率(钉尖朝下次数/试验总次数)
20
11
9
0.55
0.45
频率:在n次重复试验中,不确定事件A发生了m次,则比值称为事件A发生的频率.
讲授新课
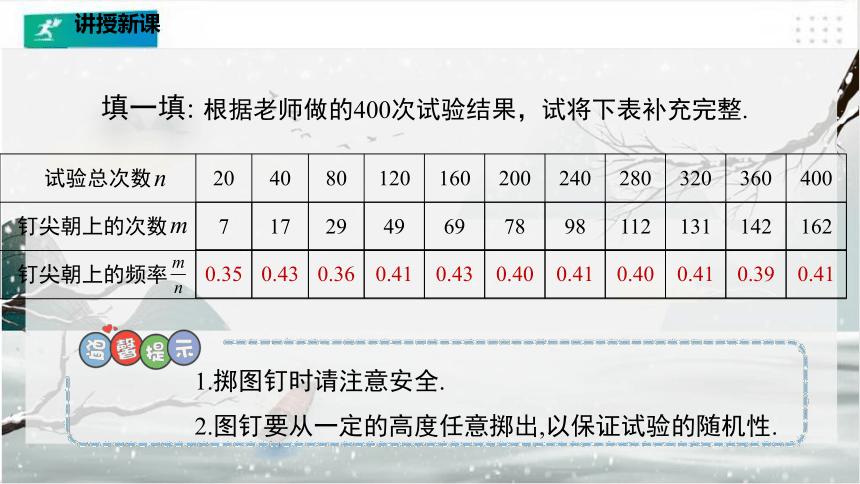
试验总次数 20 40 80 120 160 200 240 280 320 360 400
钉尖朝上的次数
钉尖朝上的频率
根据老师做的400次试验结果,试将下表补充完整.
填一填:
7 17 29 49 69 78 98 112 131 142 162
0.35 0.43 0.36 0.41 0.43 0.40 0.41 0.40 0.41 0.39 0.41
1.掷图钉时请注意安全.
2.图钉要从一定的高度任意掷出,以保证试验的随机性.
讲授新课
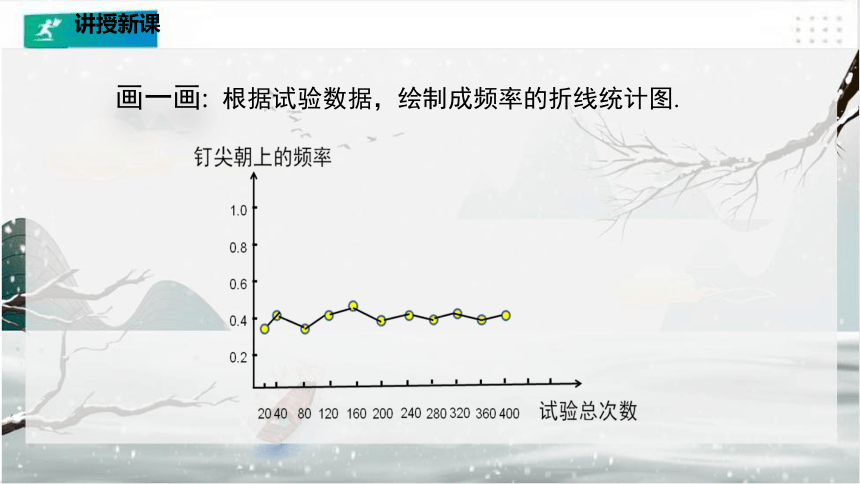
画一画:
根据试验数据,绘制成频率的折线统计图.
讲授新课
观察该折线图,钉尖朝上的频率的变化有什么规律?
看一看:
一开始的时候频率相差较大,随着试验次数越来越多,频率相差的值越来越小.
试验的次数较小时,折线上下摆动的幅度可能比较大;但当试验的次数很大时,折线的波动幅度越来越小,频率越来越稳定.
当试验次数很大时,钉尖朝上的频率,都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
讲授新课
议一议:
(1)通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎样想的?
(2)小军和小凡一起做了1000次掷图钉的试验,其中有640次钉尖朝上.据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大.你同意他们的说法吗?
不一样大,因为针尖朝上频率稳定在0.4左右.
他们的说法是有一定道理的.在试验次数很大(1000次)的情况下,有640次钉尖朝上,360次钉尖朝下,我们有理由认为钉尖朝上的可能性比钉尖朝下的可能性大.
讲授新课
例1.(1)掷一枚质地均匀的硬币10次,下列说法正确的是 ( )
A.每两次必有1次正面向上 B.可能有5次正面向上
C.必有5次正面向上 D.不可能有10次正面向上
(2)某种彩票的中奖机会是1%,下列说法正确的是 ( )
A.买一张这种彩票一定不会中奖
B.买一张这种彩票一定会中奖
C.买100张这种彩票一定会中奖
D.当购买彩票的数量很大时,中奖的频率稳定在1%
B
D
讲授新课
例2.王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据(结果保留两位小数):
摸球的次数n 100 150 200 500 800 1000
摸到黑球的次数m 23 31 60 130 203 251
摸到黑球的频率 0.23 0.21 0.30 0.26 0.25 ____
讲授新课
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________;
(2)估算袋中白球的个数.
解:(1)251÷1000≈0.25.∵大量重复试验事件发生的频率逐渐稳定到0.25附近,∴估计从袋中摸出一个球是黑球的概率是0.25;
(2)设袋中白球为x个, =0.25,x=3.
答:估计袋中有3个白球.
当堂检测
1.在综合实践活动中,小明、小亮、小颖、小菁四位同学用投掷一枚图钉的方法估计顶尖朝上的概率,他们试验次数分别为20次、50次、150次、200次,其中,试验相对科学的同学是( )
A.小明 B.小亮
C.小颖 D.小菁
D
当堂检测
2.在一个不透明的布袋中装有红色、白色玻璃球共40个,除颜色外其他完全相同,小明通过多次摸球试验后发观,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能有( )
A.4个 B.6个
C.34个 D.36个
B
当堂检测
3.为了看图钉落地后钉尖着地的频率有多大,小明做了大量重复试验,发现钉尖着地的次数是实验总次数的40%,下列说法错误的是( )
A.钉尖着地的频率是0.4
B.前20次试验结束后,钉尖着地的次数一定是8次
C.随着试验次数的增加,钉尖着地的频率稳定在0.4附近
D.钉尖着地的可能性小于钉尖朝上的可能性
B
当堂检测
5.一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
______
(1)请将表中数据补充完整,并画出折线统计图中剩余部分.
实验次数 20 40 60 80 100 120 140 160
“車”字朝上的次数 14 18 38 47 52 ___ 77 88
“車”字朝上的频率 0.7 0.45 0.63 0.59 0.52 0.55 0.56 ___
66
0.55
当堂检测
(2)如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,请估计这个机会约是多少?
答:这个机会约是0.55.
当堂检测
6.一粒木质中国象棋棋子“兵”,它的正面雕刻一个“兵”字,反面是平的.将它从一定的高度掷下,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,因此某试验小组做了棋子下掷试验,试验结果如下表:
试验次数(n) 20 40 60 80 100 120 140 160
“兵”字面朝上的次数(m) 14 38 47 52 66 78
相应的频率 0.7 0.45 0.59 0.52 0.56 0.55
当堂检测
(1)请将数据表补充完整;
(2)根据上表画出“兵”字面朝上的频率分布折线统计图;
(3)试验继续进行下去,根据上表的数据,这个试验的频率将趋于稳定,这个稳定值是多少?
解:(1)从左向右依次填:18、0.63、0.55、88;
(2)折线图如图所示.
(3)根据表中数据,试验频率分别为0.7、0.45、0.63、0.59、0.52、0.55、0.56、0.55,稳定在0.55左右,故这个稳定值为0.55.
课堂小结
1.频率及其稳定性:
通过试验让学生理解当试验次数较大时,试验的频率具有稳定性,并据此能初步估计出某一事件发生的可能性大小.
2.频率定义:在n次重复试验中,不确定事件A发生了m次,则比值称为事件发生的频率.
https://www.21cnjy.com/help/help_extract.php
6.2.1频率的稳定性(1)
第六章
概率初步
七年级数学下册同步(北师大版)
学习目标
1.通过试验让学生理解当试验次数较大时,实验的频率具有稳定性,并据此能初步估计出某一事件发生的可能性大小。
2.大量重复试验得到频率的稳定值的分析。
导入新课
在一定条件下可能发生也可能不发生的事件,叫做随机事件,也称为为不确定事件。
注意:不可能事件是属于确定事件而不属于不确定事件。
1.什么是必然事件?
在一定条件下一定会发生的事件,称为必然事件
2.什么是不可能事件?
在一定条件下一定不会发生的事件称为不可能事件
3.什么是确定的事件?
必然事件与不可能事件统称为确定的事件
4.什么是不确定事件?
导入新课
周末,小明和小军在家制作照片墙,但是图钉不够用,派谁去买呢?于是小明提出掷图钉的建议:掷一枚图钉,落地后会出现两种情况,如果钉尖朝上,小军去;如果钉尖朝下,小明去.
直觉告诉我,任意掷一枚图钉,钉尖朝上和钉尖朝下的可能性是不相同的.
其实我的直觉和你一样,但我不知道对不对.
讲授新课
频率的稳定性
你认为钉尖朝上和钉尖朝下的可能性一样大吗?
不确定,要看图钉的材质
可能一样吧~
钉尖朝上的可能性大,图钉钉帽看起来比较重,更容易与地面接触
不妨让我们用试验来验证吧!
讲授新课
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
试验总次数
钉尖朝上次数
钉尖朝下次数
钉尖朝上频率(钉尖朝上次数/试验总次数)
钉尖朝下频率(钉尖朝下次数/试验总次数)
20
11
9
0.55
0.45
频率:在n次重复试验中,不确定事件A发生了m次,则比值称为事件A发生的频率.
讲授新课
试验总次数 20 40 80 120 160 200 240 280 320 360 400
钉尖朝上的次数
钉尖朝上的频率
根据老师做的400次试验结果,试将下表补充完整.
填一填:
7 17 29 49 69 78 98 112 131 142 162
0.35 0.43 0.36 0.41 0.43 0.40 0.41 0.40 0.41 0.39 0.41
1.掷图钉时请注意安全.
2.图钉要从一定的高度任意掷出,以保证试验的随机性.
讲授新课
画一画:
根据试验数据,绘制成频率的折线统计图.
讲授新课
观察该折线图,钉尖朝上的频率的变化有什么规律?
看一看:
一开始的时候频率相差较大,随着试验次数越来越多,频率相差的值越来越小.
试验的次数较小时,折线上下摆动的幅度可能比较大;但当试验的次数很大时,折线的波动幅度越来越小,频率越来越稳定.
当试验次数很大时,钉尖朝上的频率,都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
讲授新课
议一议:
(1)通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎样想的?
(2)小军和小凡一起做了1000次掷图钉的试验,其中有640次钉尖朝上.据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大.你同意他们的说法吗?
不一样大,因为针尖朝上频率稳定在0.4左右.
他们的说法是有一定道理的.在试验次数很大(1000次)的情况下,有640次钉尖朝上,360次钉尖朝下,我们有理由认为钉尖朝上的可能性比钉尖朝下的可能性大.
讲授新课
例1.(1)掷一枚质地均匀的硬币10次,下列说法正确的是 ( )
A.每两次必有1次正面向上 B.可能有5次正面向上
C.必有5次正面向上 D.不可能有10次正面向上
(2)某种彩票的中奖机会是1%,下列说法正确的是 ( )
A.买一张这种彩票一定不会中奖
B.买一张这种彩票一定会中奖
C.买100张这种彩票一定会中奖
D.当购买彩票的数量很大时,中奖的频率稳定在1%
B
D
讲授新课
例2.王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据(结果保留两位小数):
摸球的次数n 100 150 200 500 800 1000
摸到黑球的次数m 23 31 60 130 203 251
摸到黑球的频率 0.23 0.21 0.30 0.26 0.25 ____
讲授新课
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________;
(2)估算袋中白球的个数.
解:(1)251÷1000≈0.25.∵大量重复试验事件发生的频率逐渐稳定到0.25附近,∴估计从袋中摸出一个球是黑球的概率是0.25;
(2)设袋中白球为x个, =0.25,x=3.
答:估计袋中有3个白球.
当堂检测
1.在综合实践活动中,小明、小亮、小颖、小菁四位同学用投掷一枚图钉的方法估计顶尖朝上的概率,他们试验次数分别为20次、50次、150次、200次,其中,试验相对科学的同学是( )
A.小明 B.小亮
C.小颖 D.小菁
D
当堂检测
2.在一个不透明的布袋中装有红色、白色玻璃球共40个,除颜色外其他完全相同,小明通过多次摸球试验后发观,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能有( )
A.4个 B.6个
C.34个 D.36个
B
当堂检测
3.为了看图钉落地后钉尖着地的频率有多大,小明做了大量重复试验,发现钉尖着地的次数是实验总次数的40%,下列说法错误的是( )
A.钉尖着地的频率是0.4
B.前20次试验结束后,钉尖着地的次数一定是8次
C.随着试验次数的增加,钉尖着地的频率稳定在0.4附近
D.钉尖着地的可能性小于钉尖朝上的可能性
B
当堂检测
5.一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
______
(1)请将表中数据补充完整,并画出折线统计图中剩余部分.
实验次数 20 40 60 80 100 120 140 160
“車”字朝上的次数 14 18 38 47 52 ___ 77 88
“車”字朝上的频率 0.7 0.45 0.63 0.59 0.52 0.55 0.56 ___
66
0.55
当堂检测
(2)如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,请估计这个机会约是多少?
答:这个机会约是0.55.
当堂检测
6.一粒木质中国象棋棋子“兵”,它的正面雕刻一个“兵”字,反面是平的.将它从一定的高度掷下,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,因此某试验小组做了棋子下掷试验,试验结果如下表:
试验次数(n) 20 40 60 80 100 120 140 160
“兵”字面朝上的次数(m) 14 38 47 52 66 78
相应的频率 0.7 0.45 0.59 0.52 0.56 0.55
当堂检测
(1)请将数据表补充完整;
(2)根据上表画出“兵”字面朝上的频率分布折线统计图;
(3)试验继续进行下去,根据上表的数据,这个试验的频率将趋于稳定,这个稳定值是多少?
解:(1)从左向右依次填:18、0.63、0.55、88;
(2)折线图如图所示.
(3)根据表中数据,试验频率分别为0.7、0.45、0.63、0.59、0.52、0.55、0.56、0.55,稳定在0.55左右,故这个稳定值为0.55.
课堂小结
1.频率及其稳定性:
通过试验让学生理解当试验次数较大时,试验的频率具有稳定性,并据此能初步估计出某一事件发生的可能性大小.
2.频率定义:在n次重复试验中,不确定事件A发生了m次,则比值称为事件发生的频率.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
