6.3.4 等可能事件的概率(4)(课件)(共20张PPT)
文档属性
| 名称 | 6.3.4 等可能事件的概率(4)(课件)(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 19:55:23 | ||
图片预览







文档简介
(共20张PPT)
6.3.4等可能事件的概率(4)
第六章
概率初步
七年级数学下册同步(北师大版)
学习目标
1.会进行简单的概率计算,了解概率的大小与面积
的关系,能设计符合要求的简单概率模型;
2.初步认识概率与人类生活的密切联系,感受概率
的应用价值.
导入新课
设一个试验的所有可能结果有n种,每次试验有且只有其中一种结果.如果每种结果出现的可能性相同,那么我们称这个试验的结果是等可能的.
例如:①抛一枚硬币正面朝上和反面朝上;②抓阄游戏;
③抽签游戏;④掷骰子游戏 ; ⑤抽扑克牌游戏;
⑥摸球游戏;⑦转盘游戏(转盘均分).
双方的获胜的概率要相同
2.游戏的公平性:
1.等可能事件:
导入新课
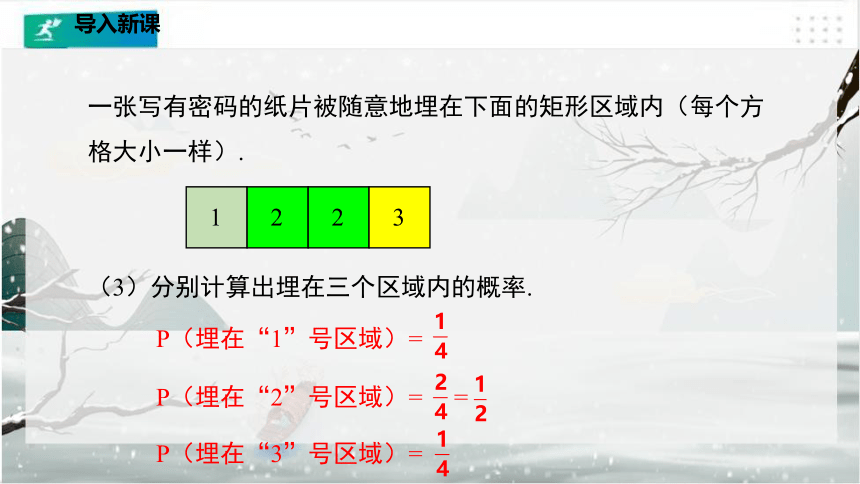
一张写有密码的纸片被随意地埋在下面的矩形区域内(每个方格大小一样).
(1)埋在哪个区域的可能性大?
(2)埋在哪两个区域的概率相同?
1
2
2
3
埋在“2”号区域的可能性大.
埋在“1”号和“3”号区域的概率相同.
导入新课
一张写有密码的纸片被随意地埋在下面的矩形区域内(每个方格大小一样).
(3)分别计算出埋在三个区域内的概率.
1
2
2
3
P(埋在“2”号区域)= =
P(埋在“1”号区域)=
P(埋在“3”号区域)=
讲授新课
与面积相关的等可能事件概率
如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?
红
120°
白
指针不是落在红色区域就是落在白色区域,
落在红色区域和白色区域的概率相等,所以
P(落在红色区域)=P(落在白色区域)= .
把可能性不同的情况当成等可能性的情况处理,这是错误的.
小明
讲授新课
红
120°
白
先把白色区域等分成2份,这样转盘被分成
3个扇形区域,其中1个是红色,2个是白色,
所以 P(落在红色区域)= ,
P(落在白色区域) = .
小颖
如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?
讲授新课
红
120°
白
利用圆心角度数计算,所以
P(落在红色区域)= ,
P(落在白色区域)= .
小亮
如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?
讲授新课
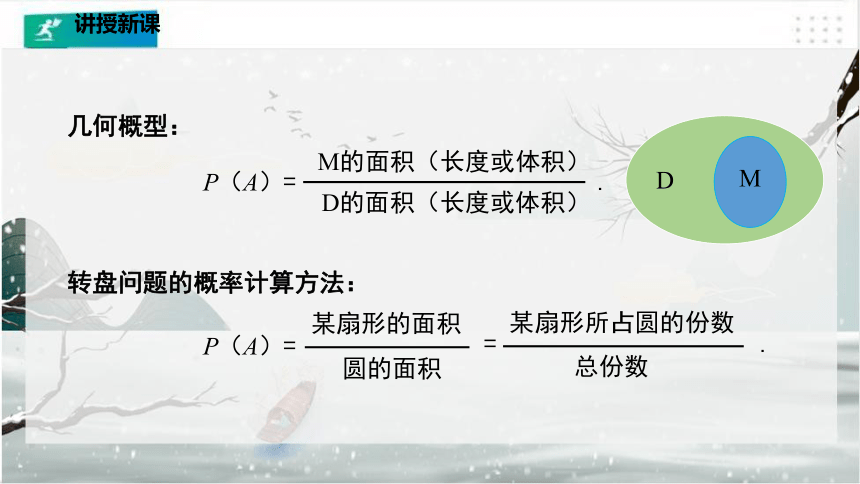
几何概型:
转盘问题的概率计算方法:
P(A)=
某扇形的面积
圆的面积
P(A)= .
M的面积(长度或体积)
D的面积(长度或体积)
= .
某扇形所占圆的份数
总份数
D
M
讲授新课
转动如图所示的转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?你有什么方法?与同伴进行交流.
根据你对前面知识的学习,你能将非等可能性转化为等可能行吗 提示:需要两部分的标准一致
提示:
两部分每份都是1o,或2o,或5o,或10o等,只要等分的标准一致就行
(此类型通常按1o方便直接)
红
120°
白
讲授新课
例: 某路口南北方向红绿灯的设置时间为:红灯20秒、绿灯60
秒、黄灯3秒.小明的爸爸随机地由南往北开车经过该路口,问:
(1)他遇到红灯的概率大还是遇到绿灯的概率大?
(2)他遇到红灯的概率是多少?
解:(1)小明的爸爸随机地到达该路口,他每一时刻到达的可能性都相同. 因为该路口南北方向红绿灯的设置时间为:红灯40s、绿灯60s、黄灯3s.绿灯时间比红灯时间长,所以他遇到绿灯的概率大.
(2)他遇到红灯的概率为:
当堂检测
1.小明、小亮、小冬三名男生结伴出游投宿一家旅馆,该旅馆只有一人间和二人间,则小明住单人间的概率为( )
A. B. C. D.无法确定
2.100件产品中有97件正品,3件次品,今从中任取一件得到次品的概率是( )
A. B. C. D.
A
A
当堂检测
3.如右图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上相应的颜色,转动转盘,转盘停止后,指针指向蓝色区域的概率是( ).
A. B. C. D.
B
当堂检测
4.3张飞机票,2张火车票,分别放在五个相同的盒子中,小亮从中任取一个盒子决定出游方式,那么他乘飞机出游的概率是_____.
5.在5升水中有一个病毒,现从中随机地取出一升水,含有病毒的概率是 .
当堂检测
6.如右图,转盘被等分成六个扇形区域,在上面依次写上1、2、3、4、5、6,转盘指针的位置固定,转动转盘后任其自由停止。问:
(1)当停止转动时,指针指向奇数区域的概率是多少
(2)请你用这个转盘设计一个游戏(六等分扇形不变),
使自由转动的转盘停止时,指针指向的区域的概率为 ,
并说明你的设计理由.
(设计方案可用图示表示,也可以用文字表述)
当堂检测
解:(1)当转盘停止转动时,指针指向数字区域1,2,3,4,5,6的机会是均等的,故共有6种均等的结果,其中指针可指向奇数区域1,3,5有3种结果,
∴P(奇数)= .所以,转盘停止时,指针指向奇数区域的概率是 .
当堂检测
(2)可在转盘的6个小扇形中,将其中的任意4个填涂成同一种颜色即可,因为转盘停止转动后,指针指向任何一个小扇形区域的机会均等,其概率为 ,而图中有4个小扇形涂成了同一种颜色,即指针指向这种颜色区域的概率为4× = .
课堂小结
1. 与面积相关的等可能事件概率的求法:
事件A的概率等于事件A所包含的图形面积m与图形总面积n的比P(A)= .
2.几何面积概率P=
利用此公式时,若所给图形能等分成若干份,可按份数直接计算;若不能,则设法求出各自的面积.
https://www.21cnjy.com/help/help_extract.php
6.3.4等可能事件的概率(4)
第六章
概率初步
七年级数学下册同步(北师大版)
学习目标
1.会进行简单的概率计算,了解概率的大小与面积
的关系,能设计符合要求的简单概率模型;
2.初步认识概率与人类生活的密切联系,感受概率
的应用价值.
导入新课
设一个试验的所有可能结果有n种,每次试验有且只有其中一种结果.如果每种结果出现的可能性相同,那么我们称这个试验的结果是等可能的.
例如:①抛一枚硬币正面朝上和反面朝上;②抓阄游戏;
③抽签游戏;④掷骰子游戏 ; ⑤抽扑克牌游戏;
⑥摸球游戏;⑦转盘游戏(转盘均分).
双方的获胜的概率要相同
2.游戏的公平性:
1.等可能事件:
导入新课
一张写有密码的纸片被随意地埋在下面的矩形区域内(每个方格大小一样).
(1)埋在哪个区域的可能性大?
(2)埋在哪两个区域的概率相同?
1
2
2
3
埋在“2”号区域的可能性大.
埋在“1”号和“3”号区域的概率相同.
导入新课
一张写有密码的纸片被随意地埋在下面的矩形区域内(每个方格大小一样).
(3)分别计算出埋在三个区域内的概率.
1
2
2
3
P(埋在“2”号区域)= =
P(埋在“1”号区域)=
P(埋在“3”号区域)=
讲授新课
与面积相关的等可能事件概率
如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?
红
120°
白
指针不是落在红色区域就是落在白色区域,
落在红色区域和白色区域的概率相等,所以
P(落在红色区域)=P(落在白色区域)= .
把可能性不同的情况当成等可能性的情况处理,这是错误的.
小明
讲授新课
红
120°
白
先把白色区域等分成2份,这样转盘被分成
3个扇形区域,其中1个是红色,2个是白色,
所以 P(落在红色区域)= ,
P(落在白色区域) = .
小颖
如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?
讲授新课
红
120°
白
利用圆心角度数计算,所以
P(落在红色区域)= ,
P(落在白色区域)= .
小亮
如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?
讲授新课
几何概型:
转盘问题的概率计算方法:
P(A)=
某扇形的面积
圆的面积
P(A)= .
M的面积(长度或体积)
D的面积(长度或体积)
= .
某扇形所占圆的份数
总份数
D
M
讲授新课
转动如图所示的转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?你有什么方法?与同伴进行交流.
根据你对前面知识的学习,你能将非等可能性转化为等可能行吗 提示:需要两部分的标准一致
提示:
两部分每份都是1o,或2o,或5o,或10o等,只要等分的标准一致就行
(此类型通常按1o方便直接)
红
120°
白
讲授新课
例: 某路口南北方向红绿灯的设置时间为:红灯20秒、绿灯60
秒、黄灯3秒.小明的爸爸随机地由南往北开车经过该路口,问:
(1)他遇到红灯的概率大还是遇到绿灯的概率大?
(2)他遇到红灯的概率是多少?
解:(1)小明的爸爸随机地到达该路口,他每一时刻到达的可能性都相同. 因为该路口南北方向红绿灯的设置时间为:红灯40s、绿灯60s、黄灯3s.绿灯时间比红灯时间长,所以他遇到绿灯的概率大.
(2)他遇到红灯的概率为:
当堂检测
1.小明、小亮、小冬三名男生结伴出游投宿一家旅馆,该旅馆只有一人间和二人间,则小明住单人间的概率为( )
A. B. C. D.无法确定
2.100件产品中有97件正品,3件次品,今从中任取一件得到次品的概率是( )
A. B. C. D.
A
A
当堂检测
3.如右图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上相应的颜色,转动转盘,转盘停止后,指针指向蓝色区域的概率是( ).
A. B. C. D.
B
当堂检测
4.3张飞机票,2张火车票,分别放在五个相同的盒子中,小亮从中任取一个盒子决定出游方式,那么他乘飞机出游的概率是_____.
5.在5升水中有一个病毒,现从中随机地取出一升水,含有病毒的概率是 .
当堂检测
6.如右图,转盘被等分成六个扇形区域,在上面依次写上1、2、3、4、5、6,转盘指针的位置固定,转动转盘后任其自由停止。问:
(1)当停止转动时,指针指向奇数区域的概率是多少
(2)请你用这个转盘设计一个游戏(六等分扇形不变),
使自由转动的转盘停止时,指针指向的区域的概率为 ,
并说明你的设计理由.
(设计方案可用图示表示,也可以用文字表述)
当堂检测
解:(1)当转盘停止转动时,指针指向数字区域1,2,3,4,5,6的机会是均等的,故共有6种均等的结果,其中指针可指向奇数区域1,3,5有3种结果,
∴P(奇数)= .所以,转盘停止时,指针指向奇数区域的概率是 .
当堂检测
(2)可在转盘的6个小扇形中,将其中的任意4个填涂成同一种颜色即可,因为转盘停止转动后,指针指向任何一个小扇形区域的机会均等,其概率为 ,而图中有4个小扇形涂成了同一种颜色,即指针指向这种颜色区域的概率为4× = .
课堂小结
1. 与面积相关的等可能事件概率的求法:
事件A的概率等于事件A所包含的图形面积m与图形总面积n的比P(A)= .
2.几何面积概率P=
利用此公式时,若所给图形能等分成若干份,可按份数直接计算;若不能,则设法求出各自的面积.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
