苏科版数学九年级上册 2.4 第1课时 圆周角的概念与性质 同步课件(共19张PPT)
文档属性
| 名称 | 苏科版数学九年级上册 2.4 第1课时 圆周角的概念与性质 同步课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 319.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 00:00:00 | ||
图片预览

文档简介
(共19张PPT)
第2章 对称图形——圆
2.4 第1课时 圆周角的概念与性质
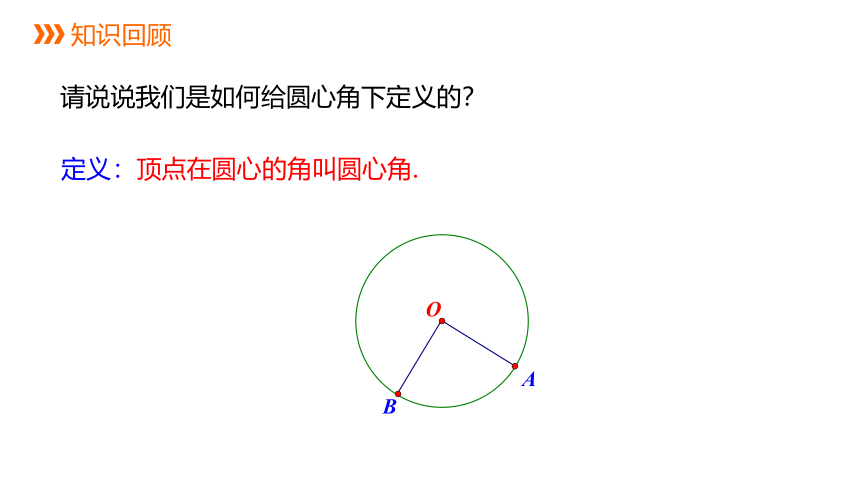
请说说我们是如何给圆心角下定义的?
定义:顶点在圆心的角叫圆心角.
O
A
B
知识回顾
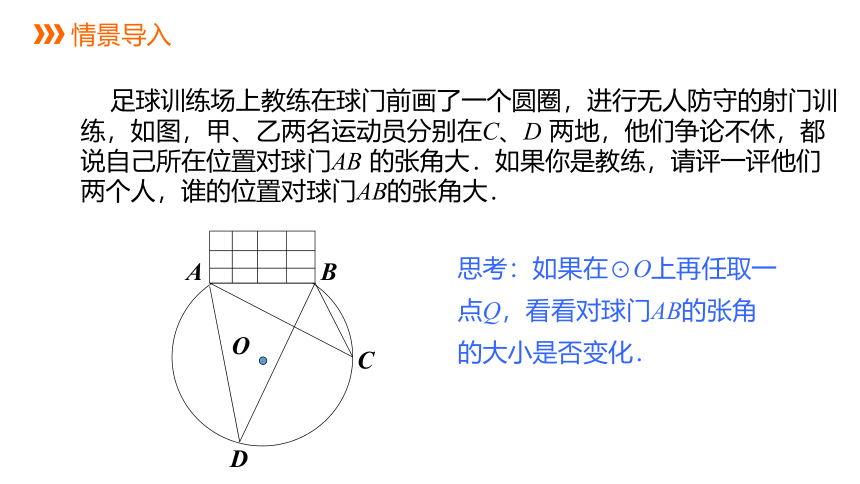
足球训练场上教练在球门前画了一个圆圈,进行无人防守的射门训练,如图,甲、乙两名运动员分别在C、D 两地,他们争论不休,都说自己所在位置对球门AB 的张角大.如果你是教练,请评一评他们两个人,谁的位置对球门AB的张角大.
A
B
O
C
D
思考:如果在⊙O上再任取一点Q,看看对球门AB的张角的大小是否变化.
情景导入
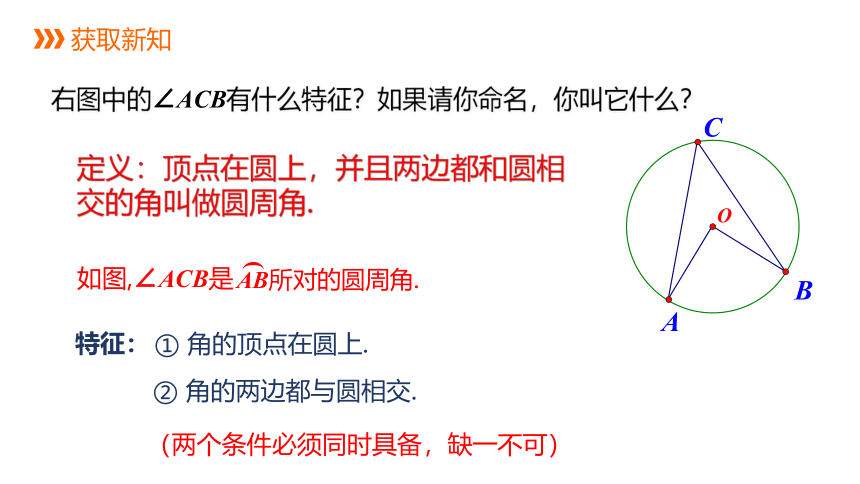
定义:顶点在圆上,并且两边都和圆相交的角叫做圆周角.
O
A
B
C
右图中的∠ACB有什么特征?如果请你命名,你叫它什么?
获取新知
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
(两个条件必须同时具备,缺一不可)
如图,∠ACB是
(
AB所对的圆周角.
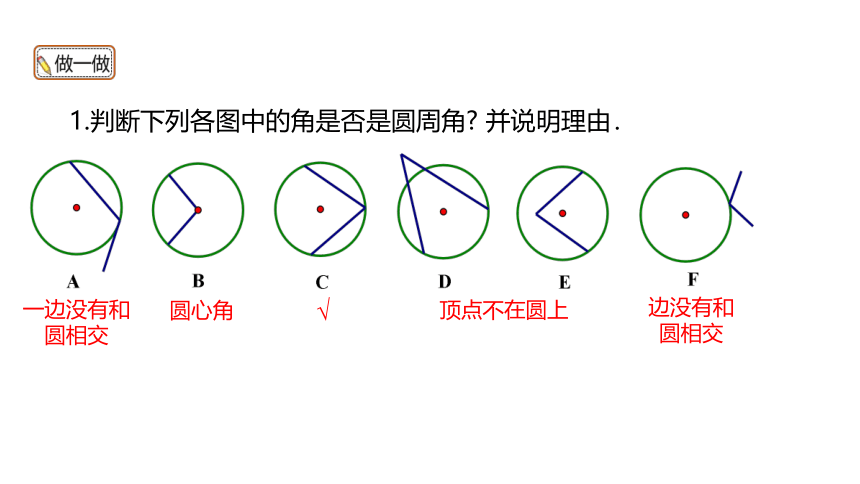
1.判断下列各图中的角是否是圆周角 并说明理由.
√
顶点不在圆上
圆心角
一边没有和圆相交
边没有和圆相交
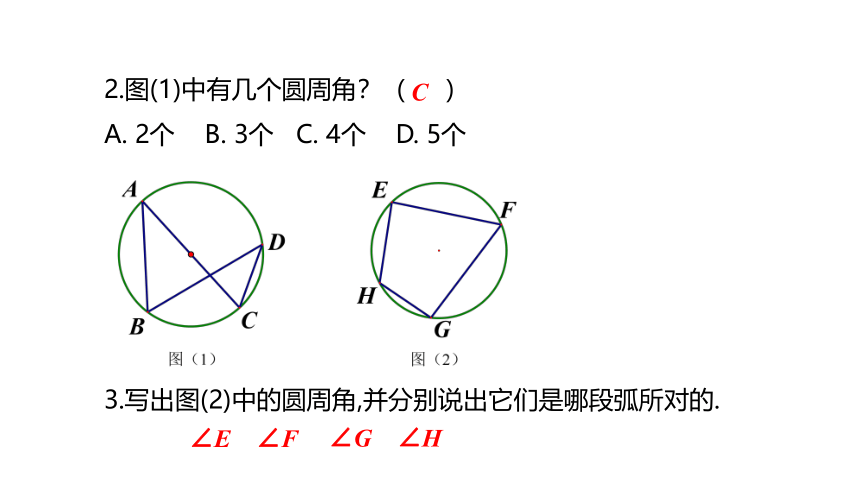
2.图(1)中有几个圆周角?( )
A. 2个 B. 3个 C. 4个 D. 5个
3.写出图(2)中的圆周角,并分别说出它们是哪段弧所对的.
C
∠E ∠F
∠G ∠H
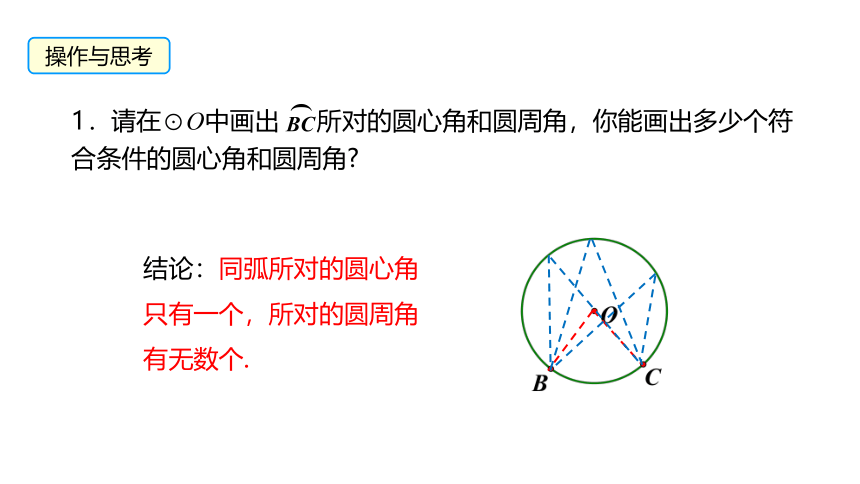
1.请在⊙O中画出 所对的圆心角和圆周角,你能画出多少个符合条件的圆心角和圆周角
(
BC
结论:同弧所对的圆心角只有一个,所对的圆周角有无数个.
操作与思考
2. 所对的圆周角有无数个,观察你所画的图形,它们与圆心O有哪几种位置关系
O在∠BAC内
O在∠BAC边上
O在∠BAC外
(
BC
3.当圆心O在∠BAC的一边上时, 所对的圆周角∠BAC与圆心角∠BOC之间有怎样的数量关系?你能证明你的发现吗
(
BC
即
证明:
∵∠BOC是△AOC的外角,
∴∠BOC=∠A +∠C.
∵OA=OC ,
∴∠C=∠A .
∴∠BOC=2∠A .
发现:
4.当圆心O在∠BAC的内部或外部时, 的关系还成立吗
证明:作直径AD.
∵
∴
即
当点O在∠BAC内部时
证明:作直径AD.
即
∵
∴
当点O在∠BAC内部时
圆周角定理:
①圆周角的度数等于它所对弧上的圆心角度数的一半.
②同弧或等弧所对的圆周角相等.
注:因为圆心角的度数与它所对的弧的度数相等,所以圆周角的度数等于它所对弧度数的一半.
归纳总结
例1 如图,⊙O的弦AB、DC的延长线相交于点E,∠AOD=150°, BC为70°,求∠ABD、∠AED的度数.
例题讲解
解:在⊙O中,∵∠AOD=150°,
∴∠ABD=∠AOD=75°(圆周角的度数
等于它所对弧上的圆心角度数的一半).
∵BC为70°,
∴∠BDC=35°(圆周角的度数等于它所对弧的度数的一半).
∵∠ABD=∠AED+∠BDC,
∴∠AED=∠ABD∠BDC=75°35°=40°.
例2. 如图,⊙O的弦AB、CD的延长线相交于点P,且AB=CD.求证:PA=PC.
证明:连接AC,
∵ AB=CD,
∴
(
AB=
(
CD
∴∠C=∠A,
∴PA=PC.
(
AD=
(
CB
(
AB+ =
(
BD
(
CD+
(
BD
即
∴
1.如图1,点A、B、C、D在⊙O上,点A、D在点B、C所在直线的同侧,∠BAC=38°,则
∠BDC = °,理由是 ;
∠BOC = °,
理由是 .
76
38
同弧所对的圆周角相等
同弧所对的圆周角等于它所对的圆心角度数的一半
图1
2.图2中相等的圆周角有 .
∠A=∠ D、∠B=∠ C
图2
随堂演练
O
D
C
B
A
D
C
B
A
3.(2021 嘉峪关)如图,点A,B,C,D,E在⊙O上,AB=CD,∠AOB=42°,则∠CED=( )
A.48° B.24° C.22° D.21°
解:连接OC、OD,
∵AB=CD,∠AOB=42°,
∴∠AOB=∠COD=42°,
∴∠CED=∠COD=21°.
D
4.如图,点A、B、C在⊙O上,点D在圆外,BD交⊙O于点F,比较∠BAC与∠BDC的大小,并说明理由.
解:连接CF.
∵ ∠BFC是△DFC的一个外角,
∴ ∠BFC >∠BDC .
∵ ∠BAC=∠BFC (同弧
所对的圆周角相等).
∴ ∠BAC >∠BDC.
F
O
D
A
B
C
课堂小结
圆周角
圆周角定义
顶点在圆上,两边都与圆相交的角.
圆周角定理
圆周角的度数等于它所对弧上的圆心角度数的一半.
同弧或等弧所对的圆周角相等.
第2章 对称图形——圆
2.4 第1课时 圆周角的概念与性质
请说说我们是如何给圆心角下定义的?
定义:顶点在圆心的角叫圆心角.
O
A
B
知识回顾
足球训练场上教练在球门前画了一个圆圈,进行无人防守的射门训练,如图,甲、乙两名运动员分别在C、D 两地,他们争论不休,都说自己所在位置对球门AB 的张角大.如果你是教练,请评一评他们两个人,谁的位置对球门AB的张角大.
A
B
O
C
D
思考:如果在⊙O上再任取一点Q,看看对球门AB的张角的大小是否变化.
情景导入
定义:顶点在圆上,并且两边都和圆相交的角叫做圆周角.
O
A
B
C
右图中的∠ACB有什么特征?如果请你命名,你叫它什么?
获取新知
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
(两个条件必须同时具备,缺一不可)
如图,∠ACB是
(
AB所对的圆周角.
1.判断下列各图中的角是否是圆周角 并说明理由.
√
顶点不在圆上
圆心角
一边没有和圆相交
边没有和圆相交
2.图(1)中有几个圆周角?( )
A. 2个 B. 3个 C. 4个 D. 5个
3.写出图(2)中的圆周角,并分别说出它们是哪段弧所对的.
C
∠E ∠F
∠G ∠H
1.请在⊙O中画出 所对的圆心角和圆周角,你能画出多少个符合条件的圆心角和圆周角
(
BC
结论:同弧所对的圆心角只有一个,所对的圆周角有无数个.
操作与思考
2. 所对的圆周角有无数个,观察你所画的图形,它们与圆心O有哪几种位置关系
O在∠BAC内
O在∠BAC边上
O在∠BAC外
(
BC
3.当圆心O在∠BAC的一边上时, 所对的圆周角∠BAC与圆心角∠BOC之间有怎样的数量关系?你能证明你的发现吗
(
BC
即
证明:
∵∠BOC是△AOC的外角,
∴∠BOC=∠A +∠C.
∵OA=OC ,
∴∠C=∠A .
∴∠BOC=2∠A .
发现:
4.当圆心O在∠BAC的内部或外部时, 的关系还成立吗
证明:作直径AD.
∵
∴
即
当点O在∠BAC内部时
证明:作直径AD.
即
∵
∴
当点O在∠BAC内部时
圆周角定理:
①圆周角的度数等于它所对弧上的圆心角度数的一半.
②同弧或等弧所对的圆周角相等.
注:因为圆心角的度数与它所对的弧的度数相等,所以圆周角的度数等于它所对弧度数的一半.
归纳总结
例1 如图,⊙O的弦AB、DC的延长线相交于点E,∠AOD=150°, BC为70°,求∠ABD、∠AED的度数.
例题讲解
解:在⊙O中,∵∠AOD=150°,
∴∠ABD=∠AOD=75°(圆周角的度数
等于它所对弧上的圆心角度数的一半).
∵BC为70°,
∴∠BDC=35°(圆周角的度数等于它所对弧的度数的一半).
∵∠ABD=∠AED+∠BDC,
∴∠AED=∠ABD∠BDC=75°35°=40°.
例2. 如图,⊙O的弦AB、CD的延长线相交于点P,且AB=CD.求证:PA=PC.
证明:连接AC,
∵ AB=CD,
∴
(
AB=
(
CD
∴∠C=∠A,
∴PA=PC.
(
AD=
(
CB
(
AB+ =
(
BD
(
CD+
(
BD
即
∴
1.如图1,点A、B、C、D在⊙O上,点A、D在点B、C所在直线的同侧,∠BAC=38°,则
∠BDC = °,理由是 ;
∠BOC = °,
理由是 .
76
38
同弧所对的圆周角相等
同弧所对的圆周角等于它所对的圆心角度数的一半
图1
2.图2中相等的圆周角有 .
∠A=∠ D、∠B=∠ C
图2
随堂演练
O
D
C
B
A
D
C
B
A
3.(2021 嘉峪关)如图,点A,B,C,D,E在⊙O上,AB=CD,∠AOB=42°,则∠CED=( )
A.48° B.24° C.22° D.21°
解:连接OC、OD,
∵AB=CD,∠AOB=42°,
∴∠AOB=∠COD=42°,
∴∠CED=∠COD=21°.
D
4.如图,点A、B、C在⊙O上,点D在圆外,BD交⊙O于点F,比较∠BAC与∠BDC的大小,并说明理由.
解:连接CF.
∵ ∠BFC是△DFC的一个外角,
∴ ∠BFC >∠BDC .
∵ ∠BAC=∠BFC (同弧
所对的圆周角相等).
∴ ∠BAC >∠BDC.
F
O
D
A
B
C
课堂小结
圆周角
圆周角定义
顶点在圆上,两边都与圆相交的角.
圆周角定理
圆周角的度数等于它所对弧上的圆心角度数的一半.
同弧或等弧所对的圆周角相等.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
