苏科版数学九年级上册 2.2 第2课时 圆的轴对称性 同步课件(共19张PPT)
文档属性
| 名称 | 苏科版数学九年级上册 2.2 第2课时 圆的轴对称性 同步课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 305.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第2章 对称图形——圆
2.2 第2课时 圆的轴对称性
×
×
√
判断题
1.等弦所对的弧相等. ( )
2.等弧所对的弦相等. ( )
3.圆心角相等,所对的弦相等. ( )
知识回顾
圆是中心对称图形吗?你是如何验证的?
●O
圆是中心对称图形,圆心是它的对称中心
情景引入
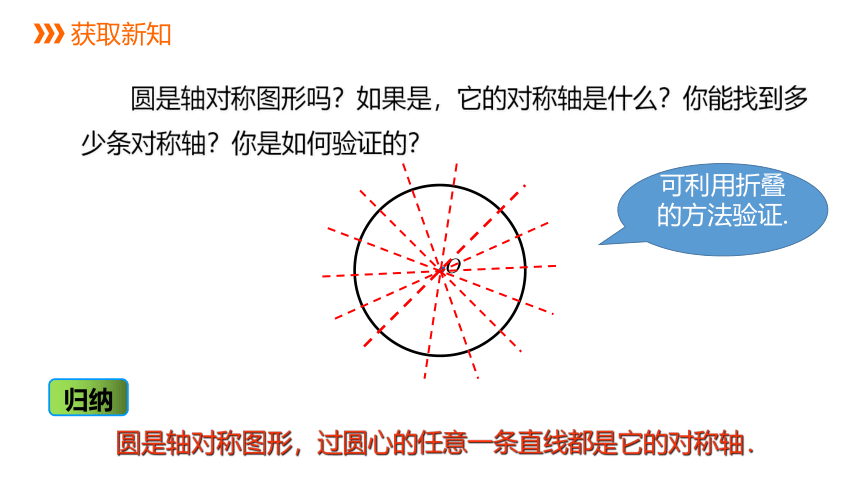
圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?你是如何验证的?
圆是轴对称图形,过圆心的任意一条直线都是它的对称轴.
●O
获取新知
可利用折叠的方法验证.
归纳
1. 如何确定圆形纸片的圆心?动手试一试!
2. 请大家在纸上画一个⊙O,再任意画一条非直径的弦AB,作一直径CD与AB垂直,交点为点P(如图).沿着直径将圆对折,你有什么发现?
●O
A
B
C
D
P└
发现:
点A与点B重合
PA与PB重合
PA=PB,
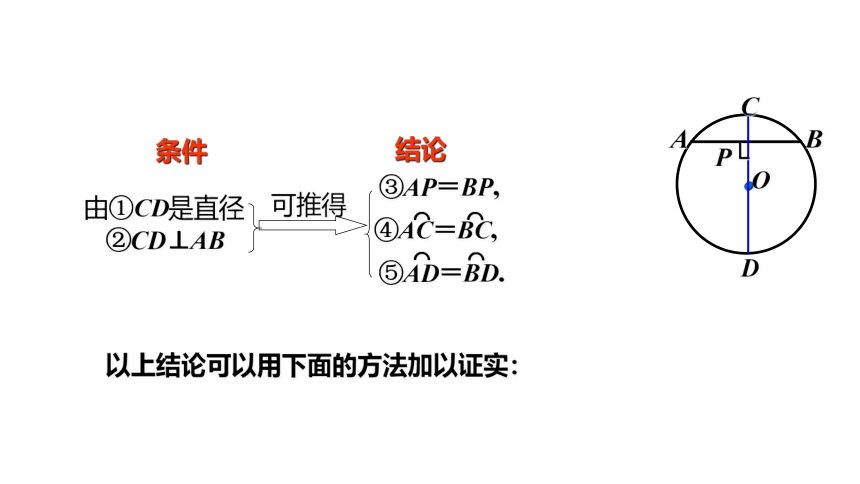
③AP=BP,
以上结论可以用下面的方法加以证实:
●O
A
B
C
D
P└
由①CD是直径
②CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
条件
结论
证明:
连接OA,OB,
● O
A
B
C
D
P└
则OA=OB.
在△OAB中,
∵OA=OB, OP⊥AB ,
∴AP=BP , ∠AOC=∠BOC,
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
∴∠AOD=∠BOD,
垂径定理: 垂直于弦的直径平分弦, 并且平分弦所对的两条弧.
●O
A
B
C
D
P└
CD⊥AB,
如图,∵ CD是直径,
∴ AP=BP,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
归纳总结
推导格式:
垂径定理的本质是:
知二得三
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分不是直径的弦
(4)这条直线平分不是直径的弦所对的优弧
(5)这条直线平分不是直径的弦所对的劣弧
1.下来图形中,哪些能使用垂径定理,为什么?
能
能
不能,因为CD没有过圆心
不能,因为两弦不垂直
垂径定理的几个基本图形:
归纳小结
必要条件:①过圆心 ;②垂直于弦.
例1. 已知:如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点,求证:AC=BD.
例题讲解
.
A
C
D
B
O
P
□
【思维点拨】可利用垂径定理来证明AC=BD.
证明:过O点作OP⊥AB,垂足为P.
∵OP⊥AB
∴PC=PD,PA=PB
∴PA-PC=PB-PD
∴AC=BD.
【常用辅助线】与弦有关的问题常过圆心作弦的垂线.
例2.已知:⊙O中弦AB∥CD,
求证:AC=BD.
⌒
⌒
.
E
C
D
A
B
O
F
证明:作直径EF⊥AB.
∵AB∥CD,∴EF⊥CD.
则AF=BF,CF=DF
(垂直弦的直径平分弦所对的弧)
AF-CF=BF-DF
∴AC=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
1.如图,⊙O直径CD与弦AB(非直径)交于点M,添加一个条件:____________,就可得到点M是AB的中点.
CD⊥AB
随堂演练
2.如图,⊙O的直径为10,弦AB=8,P为AB上的一个动点,那么OP长的取值范围_________________.
3≤OP≤5
B
A
O
P
C
3. 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径.
C
解:连接OA,过点 O作OC⊥AB,垂足为点C.
∴ ⊙O的半径为5cm.
∴AC=BC=4
∴OA=
└
4. 如图,⊙O的弦AB=8 cm,直径CE⊥AB,垂足为点D,CD=2 cm,求⊙O的半径.
●
O
A
B
E
C
D
└
∴
设OC=x cm,则OD=x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5 cm.
x2=42+(x-2)2,
解:连接OA,∵ CE⊥AB于D,
课堂小结
第2章 对称图形——圆
2.2 第2课时 圆的轴对称性
×
×
√
判断题
1.等弦所对的弧相等. ( )
2.等弧所对的弦相等. ( )
3.圆心角相等,所对的弦相等. ( )
知识回顾
圆是中心对称图形吗?你是如何验证的?
●O
圆是中心对称图形,圆心是它的对称中心
情景引入
圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?你是如何验证的?
圆是轴对称图形,过圆心的任意一条直线都是它的对称轴.
●O
获取新知
可利用折叠的方法验证.
归纳
1. 如何确定圆形纸片的圆心?动手试一试!
2. 请大家在纸上画一个⊙O,再任意画一条非直径的弦AB,作一直径CD与AB垂直,交点为点P(如图).沿着直径将圆对折,你有什么发现?
●O
A
B
C
D
P└
发现:
点A与点B重合
PA与PB重合
PA=PB,
③AP=BP,
以上结论可以用下面的方法加以证实:
●O
A
B
C
D
P└
由①CD是直径
②CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
条件
结论
证明:
连接OA,OB,
● O
A
B
C
D
P└
则OA=OB.
在△OAB中,
∵OA=OB, OP⊥AB ,
∴AP=BP , ∠AOC=∠BOC,
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
∴∠AOD=∠BOD,
垂径定理: 垂直于弦的直径平分弦, 并且平分弦所对的两条弧.
●O
A
B
C
D
P└
CD⊥AB,
如图,∵ CD是直径,
∴ AP=BP,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
归纳总结
推导格式:
垂径定理的本质是:
知二得三
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分不是直径的弦
(4)这条直线平分不是直径的弦所对的优弧
(5)这条直线平分不是直径的弦所对的劣弧
1.下来图形中,哪些能使用垂径定理,为什么?
能
能
不能,因为CD没有过圆心
不能,因为两弦不垂直
垂径定理的几个基本图形:
归纳小结
必要条件:①过圆心 ;②垂直于弦.
例1. 已知:如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点,求证:AC=BD.
例题讲解
.
A
C
D
B
O
P
□
【思维点拨】可利用垂径定理来证明AC=BD.
证明:过O点作OP⊥AB,垂足为P.
∵OP⊥AB
∴PC=PD,PA=PB
∴PA-PC=PB-PD
∴AC=BD.
【常用辅助线】与弦有关的问题常过圆心作弦的垂线.
例2.已知:⊙O中弦AB∥CD,
求证:AC=BD.
⌒
⌒
.
E
C
D
A
B
O
F
证明:作直径EF⊥AB.
∵AB∥CD,∴EF⊥CD.
则AF=BF,CF=DF
(垂直弦的直径平分弦所对的弧)
AF-CF=BF-DF
∴AC=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
1.如图,⊙O直径CD与弦AB(非直径)交于点M,添加一个条件:____________,就可得到点M是AB的中点.
CD⊥AB
随堂演练
2.如图,⊙O的直径为10,弦AB=8,P为AB上的一个动点,那么OP长的取值范围_________________.
3≤OP≤5
B
A
O
P
C
3. 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径.
C
解:连接OA,过点 O作OC⊥AB,垂足为点C.
∴ ⊙O的半径为5cm.
∴AC=BC=4
∴OA=
└
4. 如图,⊙O的弦AB=8 cm,直径CE⊥AB,垂足为点D,CD=2 cm,求⊙O的半径.
●
O
A
B
E
C
D
└
∴
设OC=x cm,则OD=x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5 cm.
x2=42+(x-2)2,
解:连接OA,∵ CE⊥AB于D,
课堂小结
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
