苏科版九年级上册2.5 三角形的内切圆(第3课时)课件(共16张PPT)
文档属性
| 名称 | 苏科版九年级上册2.5 三角形的内切圆(第3课时)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 199.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 22:23:26 | ||
图片预览




文档简介
(共16张PPT)
第2章 对称图形——圆
2.5 第3课时 三角形的内切圆
知识回顾
切线的判定定理:
切线的性质定理:
圆的切线垂直于经过切点的半径.
经过半径的外端并且垂直于这条半径的直线是圆的切线.
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
情景引入
可以发现,要使裁下的圆的面积最大,这个圆应该与三角形的各边都相切.
三角形的内切圆的定义:
与三角形各边都相切的圆叫三角形的内切圆.
这个三角形叫圆的外切三角形.
获取新知
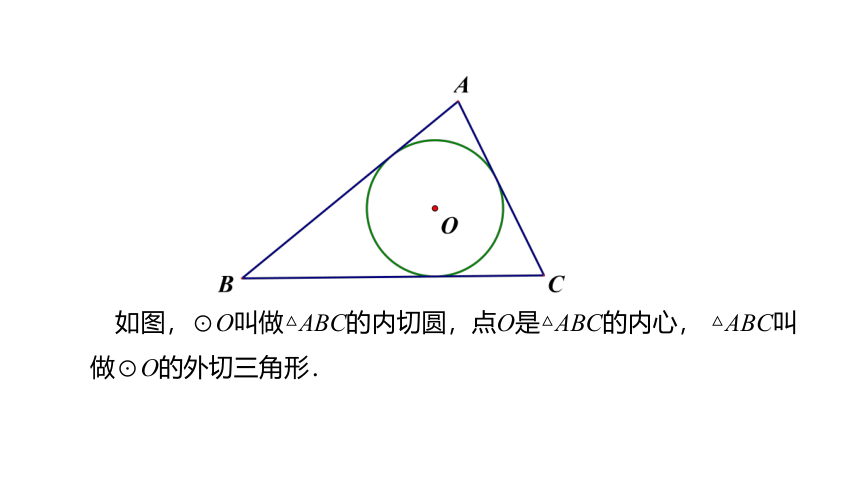
内切圆的圆心叫做三角形的内心.
如图,⊙O叫做△ABC的内切圆,点O是△ABC的内心, △ABC叫做⊙O的外切三角形.
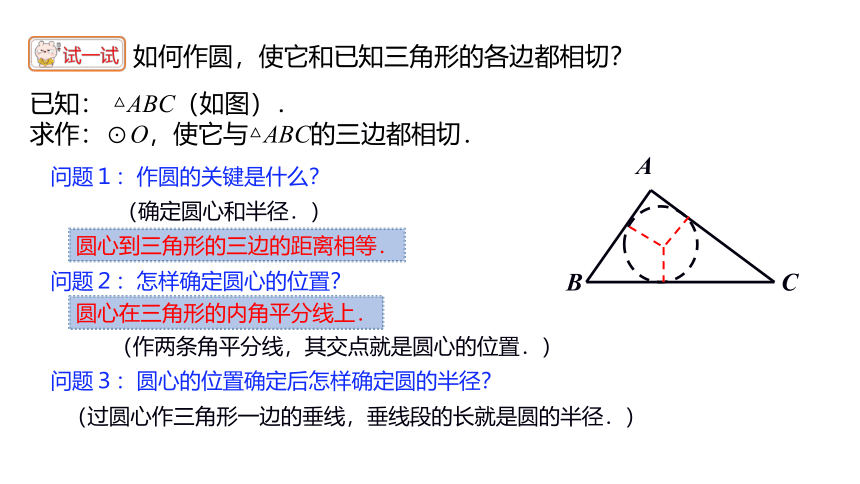
问题1:作圆的关键是什么?
问题2:怎样确定圆心的位置?
问题3:圆心的位置确定后怎样确定圆的半径?
A
B
C
(确定圆心和半径.)
(作两条角平分线,其交点就是圆心的位置.)
(过圆心作三角形一边的垂线,垂线段的长就是圆的半径.)
如何作圆,使它和已知三角形的各边都相切?
已知: △ABC(如图).
求作:⊙O,使它与△ABC的三边都相切.
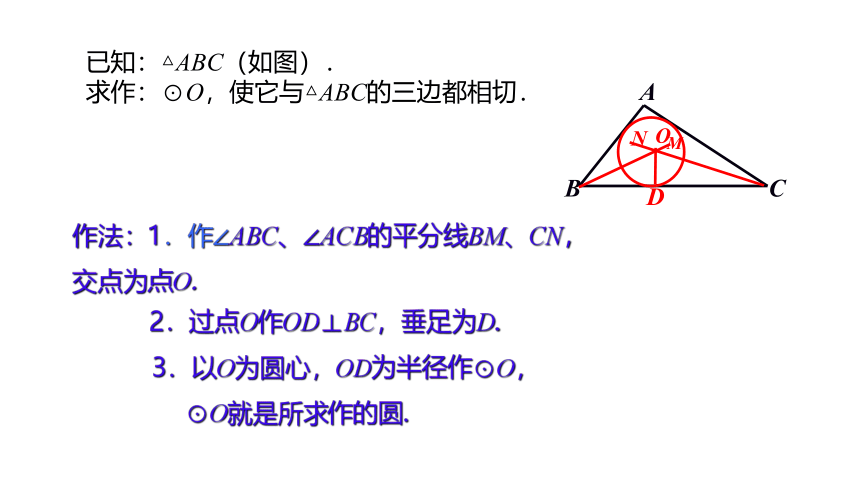
圆心到三角形的三边的距离相等.
圆心在三角形的内角平分线上.
3.以O为圆心,OD为半径作⊙O,
⊙O就是所求作的圆.
已知:△ABC(如图).
求作:⊙O,使它与△ABC的三边都相切.
A
B
C
M
N
O
D
作法:1.作∠ABC、∠ACB的平分线BM、CN,
交点为点O.
2.过点O作OD⊥BC,垂足为D.
②三角形的内心到三边的距离相等.
①三角形的内心是三角形角平分线的交点.
③三角形的内心一定在三角形的内部.
三角形内心的性质
想一想:三角形的内心有什么性质?
名称
确定
方法
图形
性质
内 心(三角形内切圆的圆心)
三角形三边垂直平分线的交点.
(1)OA=OB=OC;
(2)外心不一定在三角形的内部.
(1)到三边的距离相等;
(2)OA、OB、OC分别
平分∠BAC、∠ABC、∠ACB;
(3)内心在三角形内部.
外 心
(三角形
外接圆的
圆心)
三角形三条角平分线的交点
例 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠B=60°,∠C=70°,求∠EDF的度数.
问题:∠A与∠EDF有什么关系?
例题讲解
解:连接OE、OF. 在△ABC中,
∠A=180°-(∠B+∠C)=180°-()=50
∵ ⊙O是△ABC的内切圆,
∴ AB⊥OF,AC⊥OE.
∴ ∠EOF=360°-(∠A+∠AFO+∠AEO)
=360°-()=130
∴∠EDF∠EOF=65°.
∠A+2∠EDF=180°
1.下列说法中,正确的是( ).
A.垂直于半径的直线一定是这个圆的切线
B.三角形的外心在三角形的内部
C.三角形有且只有一个内切圆
D.三角形的内心到三角形的3个顶点的距离相等
随堂演练
C
2. 如图,点O是△ABC的内切圆的圆心,∠OAC=40°,则∠BOC的度数为( )
A.80° B.100° C.130° D.140°
C
3. 如图,点O是△ABC的内心,根据下列条件,求∠BOC的度数.
(1)∠ABC=50°, ∠ACB=60°;
(2)∠A=50°.
∠BOC=125°
∠BOC=115°
如果把题目改为:点O为△ABC的外心,∠A=50°,则∠BOC的度数又是多少?
∠BOC=100°
变式
4.(2021 毕节市)如图,⊙O是△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D,连接BD,BE.求证:DB=DE;
证明:∵点E是△ABC的内心,
∴AE平分∠BAC,BE平分∠ABC,
∴∠BAD=∠CAD,∠ABE=∠CBE,
又∵∠CAD=∠CBD.
∴∠CBD=∠BAD.
∵∠BED=∠ABE+∠BAD,∠DBE=∠CBE+∠CBD,
∴∠BED=∠DBE,
∴DB=DE.
课堂小结
三角形的
内切圆
作图
三角形内心的性质
三角形的内心是三角形角平分线的交点.
三角形的内心到三边的距离相等.
有关概念
与三角形各边都相切的圆叫三角形的内切圆.
这个三角形叫圆的外切三角形.
内切圆的圆心叫做三角形的内心.
三角形的内心一定在三角形的内部.
第2章 对称图形——圆
2.5 第3课时 三角形的内切圆
知识回顾
切线的判定定理:
切线的性质定理:
圆的切线垂直于经过切点的半径.
经过半径的外端并且垂直于这条半径的直线是圆的切线.
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
情景引入
可以发现,要使裁下的圆的面积最大,这个圆应该与三角形的各边都相切.
三角形的内切圆的定义:
与三角形各边都相切的圆叫三角形的内切圆.
这个三角形叫圆的外切三角形.
获取新知
内切圆的圆心叫做三角形的内心.
如图,⊙O叫做△ABC的内切圆,点O是△ABC的内心, △ABC叫做⊙O的外切三角形.
问题1:作圆的关键是什么?
问题2:怎样确定圆心的位置?
问题3:圆心的位置确定后怎样确定圆的半径?
A
B
C
(确定圆心和半径.)
(作两条角平分线,其交点就是圆心的位置.)
(过圆心作三角形一边的垂线,垂线段的长就是圆的半径.)
如何作圆,使它和已知三角形的各边都相切?
已知: △ABC(如图).
求作:⊙O,使它与△ABC的三边都相切.
圆心到三角形的三边的距离相等.
圆心在三角形的内角平分线上.
3.以O为圆心,OD为半径作⊙O,
⊙O就是所求作的圆.
已知:△ABC(如图).
求作:⊙O,使它与△ABC的三边都相切.
A
B
C
M
N
O
D
作法:1.作∠ABC、∠ACB的平分线BM、CN,
交点为点O.
2.过点O作OD⊥BC,垂足为D.
②三角形的内心到三边的距离相等.
①三角形的内心是三角形角平分线的交点.
③三角形的内心一定在三角形的内部.
三角形内心的性质
想一想:三角形的内心有什么性质?
名称
确定
方法
图形
性质
内 心(三角形内切圆的圆心)
三角形三边垂直平分线的交点.
(1)OA=OB=OC;
(2)外心不一定在三角形的内部.
(1)到三边的距离相等;
(2)OA、OB、OC分别
平分∠BAC、∠ABC、∠ACB;
(3)内心在三角形内部.
外 心
(三角形
外接圆的
圆心)
三角形三条角平分线的交点
例 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠B=60°,∠C=70°,求∠EDF的度数.
问题:∠A与∠EDF有什么关系?
例题讲解
解:连接OE、OF. 在△ABC中,
∠A=180°-(∠B+∠C)=180°-()=50
∵ ⊙O是△ABC的内切圆,
∴ AB⊥OF,AC⊥OE.
∴ ∠EOF=360°-(∠A+∠AFO+∠AEO)
=360°-()=130
∴∠EDF∠EOF=65°.
∠A+2∠EDF=180°
1.下列说法中,正确的是( ).
A.垂直于半径的直线一定是这个圆的切线
B.三角形的外心在三角形的内部
C.三角形有且只有一个内切圆
D.三角形的内心到三角形的3个顶点的距离相等
随堂演练
C
2. 如图,点O是△ABC的内切圆的圆心,∠OAC=40°,则∠BOC的度数为( )
A.80° B.100° C.130° D.140°
C
3. 如图,点O是△ABC的内心,根据下列条件,求∠BOC的度数.
(1)∠ABC=50°, ∠ACB=60°;
(2)∠A=50°.
∠BOC=125°
∠BOC=115°
如果把题目改为:点O为△ABC的外心,∠A=50°,则∠BOC的度数又是多少?
∠BOC=100°
变式
4.(2021 毕节市)如图,⊙O是△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D,连接BD,BE.求证:DB=DE;
证明:∵点E是△ABC的内心,
∴AE平分∠BAC,BE平分∠ABC,
∴∠BAD=∠CAD,∠ABE=∠CBE,
又∵∠CAD=∠CBD.
∴∠CBD=∠BAD.
∵∠BED=∠ABE+∠BAD,∠DBE=∠CBE+∠CBD,
∴∠BED=∠DBE,
∴DB=DE.
课堂小结
三角形的
内切圆
作图
三角形内心的性质
三角形的内心是三角形角平分线的交点.
三角形的内心到三边的距离相等.
有关概念
与三角形各边都相切的圆叫三角形的内切圆.
这个三角形叫圆的外切三角形.
内切圆的圆心叫做三角形的内心.
三角形的内心一定在三角形的内部.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
