苏科版九年级上册2.4 圆的内接四边形(第3课时)课件(共15张PPT)
文档属性
| 名称 | 苏科版九年级上册2.4 圆的内接四边形(第3课时)课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 207.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 22:36:45 | ||
图片预览





文档简介
(共15张PPT)
第2章 对称图形——圆
2.4 第3课时 圆的内接四边形
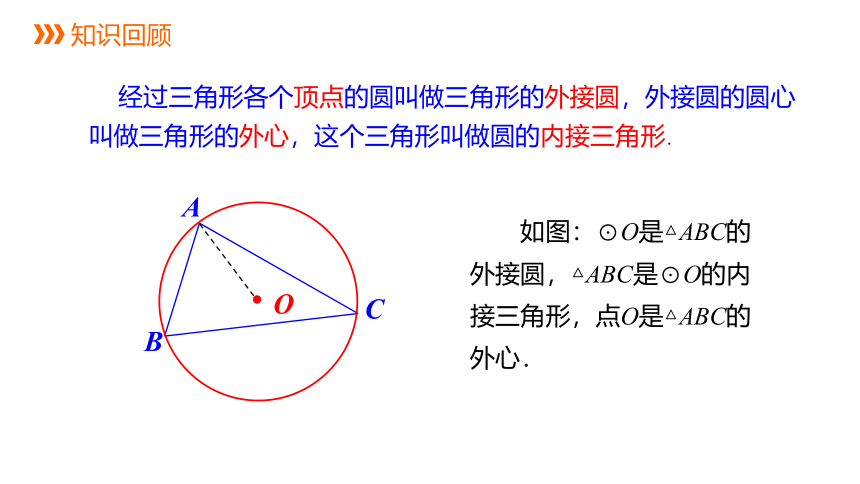
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆,△ABC是⊙O的内接三角形,点O是△ABC的外心.
C
A
B
O
知识回顾
问题1:过三角形的三个顶点能画一个圆吗?为什么?
能,经过不在同一直线上的三点可以确定一个圆.
问题2:经过四边形的四个顶点能画一个圆吗?为什么?
不一定,比如菱形的四个顶点不在同一个圆上.
情景导入
一个四边形的4个顶点都在同一个圆上,这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.
如图,四边形ABCD是 ,
⊙O是 .
⊙O的内接四边形
四边形ABCD的外接圆
获取新知
1.已知四边形ABCD是⊙O的内接四边形,当BD是直径时,你能发现∠A与∠C、∠ABC与∠ADC有怎样的数量关系?为什么?
∵ BD是⊙O的直径,
∴ ∠A=∠C=90 ,
则∠A+∠C=180 .
∵ 四边形ABCD的内角和为360 ,
∴ ∠ADC+∠ABC=360 =180 .
思考与探究
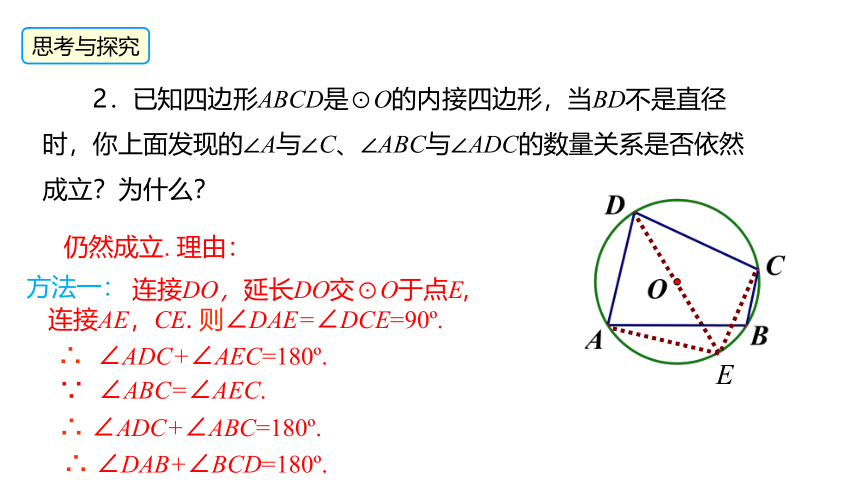
2.已知四边形ABCD是⊙O的内接四边形,当BD不是直径时,你上面发现的∠A与∠C、∠ABC与∠ADC的数量关系是否依然成立?为什么?
E
连接DO,延长DO交⊙O于点E,
连接AE,CE. 则∠DAE=∠DCE=90 .
∴ ∠ADC+∠AEC=180 .
∴ ∠ADC+∠ABC=180 .
∵ ∠ABC=∠AEC.
∴ ∠DAB+∠BCD=180 .
思考与探究
仍然成立. 理由:
方法一:
2.已知四边形ABCD是⊙O的内接四边形,当BD不是直径时,你上面发现的∠A与∠C、∠ABC与∠ADC的数量关系是否依然成立?为什么?
思考与探究
方法二:
连接OD,OB.
∴ ∠DAB+∠BCD=180 .
根据圆周角定理,可知
1
2
圆内接四边形性质定理:
圆内接四边形的对角互补.
用符号语言描述这个定理:
∵ 四边形ABCD是⊙O内接四边形,
∴ ∠A+∠C=180°,
∠B+∠D=180°.
归纳总结
∵∠A+∠DCB=180°,
∠DCB+∠DCE=180°.
∴∠A=∠DCE.
想一想
如图,∠DCE是圆内接四边形ABCD的一个外角,∠A与∠DCE的大小有何关系?
归纳:圆内接四边形的一个外角等于它的内对角.
例 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°,若点E在AD上,求∠E的度数.
例题讲解
解:连接BD,
∵四边形ABCD是⊙O的内接四边形,
∴∠B∠C=180°.
∴∠B180°∠C=180°110°=70°,
∵AB=AD,
∴∠ABD=∠ADB=.
∵四边形ABDE是⊙O的内接四边形,
∴∠∠E=180°.
∴∠180°∠ABD=180°°=125°.
随堂演练
1.(2021 常德)如图,已知四边形ABCD是圆O的内接四边形,∠BOD=80°,则∠BCD= .
140°
2.如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=115°,则另一个外角∠DAF的度数为( )
A.75° B.65° C.55° D.45°
B
3.若四边形ABCD为圆内接四边形,则下列哪个选项可能成立( )
A.∠A:∠B:∠C:∠D=1:2:3:4
B.∠A:∠B:∠C:∠D=2:3:1:4
C.∠A:∠B:∠C:∠D=3:1:2:4
D.∠A:∠B:∠C:∠D=4:3:2:1
C
4.如图,四边形ABCD是⊙O的内接四边形,AD与BC的延长线交于点E,∠DCB=100°,∠B=50°.求证:△CDE是等腰三角形.
证明:∵四边形ABCD是⊙O的内接四边形,
∴∠CDA+∠B=180°,
∵∠B=50°,
∴∠CDA=180°﹣50°=130°,
∴∠CDE=180°﹣∠CDA=180°﹣130°=50°.
∵∠DCB=100°,
∴∠CDE+∠E=100°,
∴∠E=50°,
∴∠E=∠CDE,
∴CD=CE,
∴△CDE是等腰三角形.
课堂小结
圆内接四边形的对角互补
推论:圆内接四边形的一个外角等于它的内对角.
圆的内接四边形
第2章 对称图形——圆
2.4 第3课时 圆的内接四边形
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆,△ABC是⊙O的内接三角形,点O是△ABC的外心.
C
A
B
O
知识回顾
问题1:过三角形的三个顶点能画一个圆吗?为什么?
能,经过不在同一直线上的三点可以确定一个圆.
问题2:经过四边形的四个顶点能画一个圆吗?为什么?
不一定,比如菱形的四个顶点不在同一个圆上.
情景导入
一个四边形的4个顶点都在同一个圆上,这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.
如图,四边形ABCD是 ,
⊙O是 .
⊙O的内接四边形
四边形ABCD的外接圆
获取新知
1.已知四边形ABCD是⊙O的内接四边形,当BD是直径时,你能发现∠A与∠C、∠ABC与∠ADC有怎样的数量关系?为什么?
∵ BD是⊙O的直径,
∴ ∠A=∠C=90 ,
则∠A+∠C=180 .
∵ 四边形ABCD的内角和为360 ,
∴ ∠ADC+∠ABC=360 =180 .
思考与探究
2.已知四边形ABCD是⊙O的内接四边形,当BD不是直径时,你上面发现的∠A与∠C、∠ABC与∠ADC的数量关系是否依然成立?为什么?
E
连接DO,延长DO交⊙O于点E,
连接AE,CE. 则∠DAE=∠DCE=90 .
∴ ∠ADC+∠AEC=180 .
∴ ∠ADC+∠ABC=180 .
∵ ∠ABC=∠AEC.
∴ ∠DAB+∠BCD=180 .
思考与探究
仍然成立. 理由:
方法一:
2.已知四边形ABCD是⊙O的内接四边形,当BD不是直径时,你上面发现的∠A与∠C、∠ABC与∠ADC的数量关系是否依然成立?为什么?
思考与探究
方法二:
连接OD,OB.
∴ ∠DAB+∠BCD=180 .
根据圆周角定理,可知
1
2
圆内接四边形性质定理:
圆内接四边形的对角互补.
用符号语言描述这个定理:
∵ 四边形ABCD是⊙O内接四边形,
∴ ∠A+∠C=180°,
∠B+∠D=180°.
归纳总结
∵∠A+∠DCB=180°,
∠DCB+∠DCE=180°.
∴∠A=∠DCE.
想一想
如图,∠DCE是圆内接四边形ABCD的一个外角,∠A与∠DCE的大小有何关系?
归纳:圆内接四边形的一个外角等于它的内对角.
例 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°,若点E在AD上,求∠E的度数.
例题讲解
解:连接BD,
∵四边形ABCD是⊙O的内接四边形,
∴∠B∠C=180°.
∴∠B180°∠C=180°110°=70°,
∵AB=AD,
∴∠ABD=∠ADB=.
∵四边形ABDE是⊙O的内接四边形,
∴∠∠E=180°.
∴∠180°∠ABD=180°°=125°.
随堂演练
1.(2021 常德)如图,已知四边形ABCD是圆O的内接四边形,∠BOD=80°,则∠BCD= .
140°
2.如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=115°,则另一个外角∠DAF的度数为( )
A.75° B.65° C.55° D.45°
B
3.若四边形ABCD为圆内接四边形,则下列哪个选项可能成立( )
A.∠A:∠B:∠C:∠D=1:2:3:4
B.∠A:∠B:∠C:∠D=2:3:1:4
C.∠A:∠B:∠C:∠D=3:1:2:4
D.∠A:∠B:∠C:∠D=4:3:2:1
C
4.如图,四边形ABCD是⊙O的内接四边形,AD与BC的延长线交于点E,∠DCB=100°,∠B=50°.求证:△CDE是等腰三角形.
证明:∵四边形ABCD是⊙O的内接四边形,
∴∠CDA+∠B=180°,
∵∠B=50°,
∴∠CDA=180°﹣50°=130°,
∴∠CDE=180°﹣∠CDA=180°﹣130°=50°.
∵∠DCB=100°,
∴∠CDE+∠E=100°,
∴∠E=50°,
∴∠E=∠CDE,
∴CD=CE,
∴△CDE是等腰三角形.
课堂小结
圆内接四边形的对角互补
推论:圆内接四边形的一个外角等于它的内对角.
圆的内接四边形
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
