苏科版数学九年级上册 2.6 正多边形与圆 同步课件(共23张PPT)
文档属性
| 名称 | 苏科版数学九年级上册 2.6 正多边形与圆 同步课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 350.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 11:05:59 | ||
图片预览




文档简介
(共23张PPT)
第2章 对称图形——圆
2.6 正多边形与圆
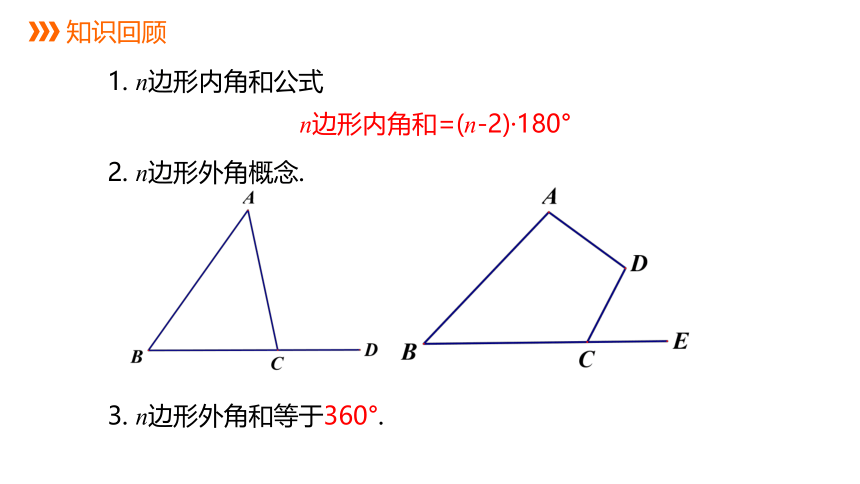
1. n边形内角和公式
2. n边形外角概念.
n边形内角和=(n-2)·180°
3. n边形外角和等于360°.
知识回顾
说说有哪些你熟悉的图形?
情景引入
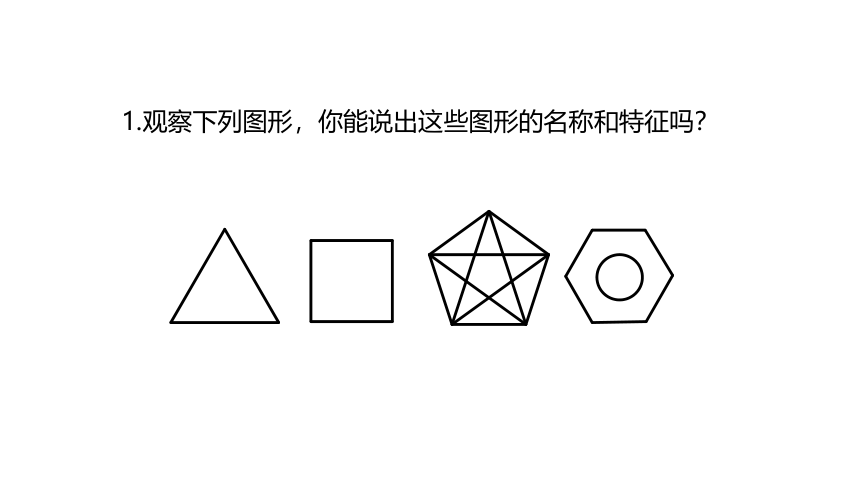
1.观察下列图形,你能说出这些图形的名称和特征吗?
各边相等、各角也相等的多边形叫做正多边形.
你能说说什么是正多边形吗?
获取新知
1. 请同学们举例,自己在日常生活中见过的正多边形.
2. 矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
思考与探索
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等.
1. 能否说各边相等的多边形是正多边形?
2. 能否说各角相等的多边形是正多边形?
注意
正多边形
缺一不可
各边相等
各角相等
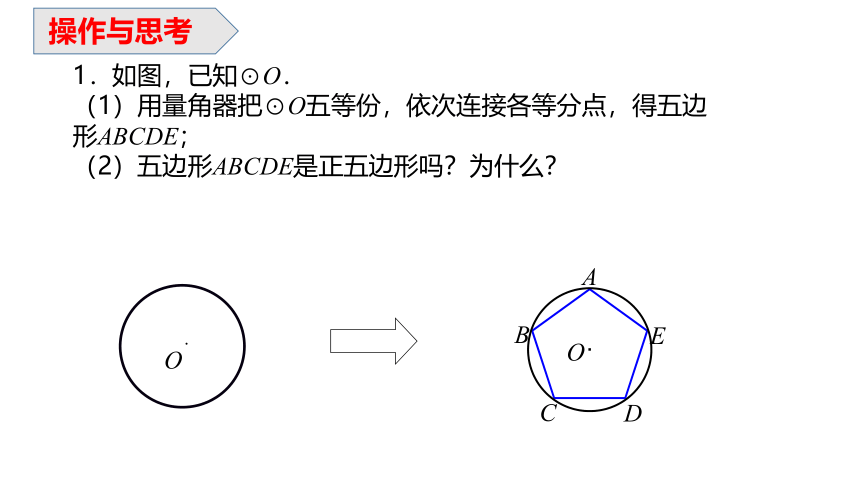
1.如图,已知⊙O.
(1)用量角器把⊙O五等份,依次连接各等分点,得五边形ABCDE;
(2)五边形ABCDE是正五边形吗?为什么?
操作与思考
·
A
B
C
D
E
O
O
.
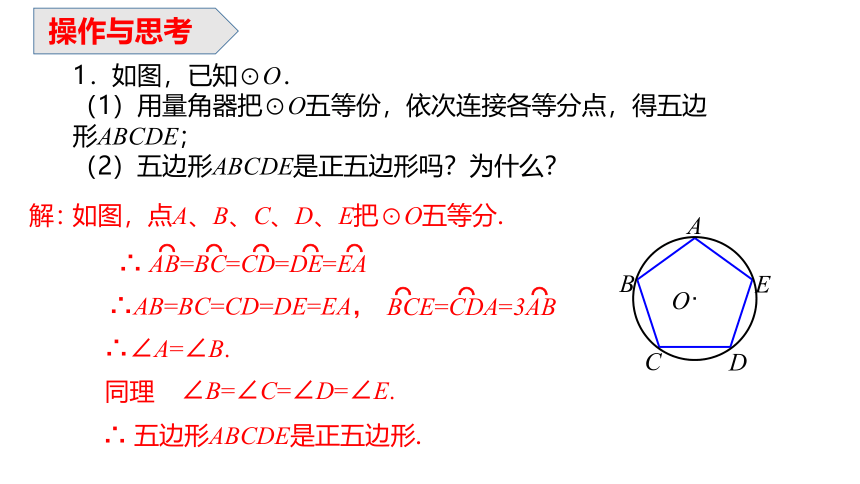
1.如图,已知⊙O.
(1)用量角器把⊙O五等份,依次连接各等分点,得五边形ABCDE;
(2)五边形ABCDE是正五边形吗?为什么?
操作与思考
·
A
B
C
D
E
O
如图,点A、B、C、D、E把⊙O五等分.
解:
∴ AB=BC=CD=DE=EA
⌒
⌒
⌒
⌒
⌒
∴AB=BC=CD=DE=EA,
BCE=CDA=3AB
⌒
⌒
⌒
∴∠A=∠B.
同理
∠B=∠C=∠D=∠E.
∴ 五边形ABCDE是正五边形.
2. 如图,点A、B、C、D、E、F六等分⊙O.
(1)在一张透明纸上画与下图形状、大小相同的图形,并把它们叠合在一起;
(2)把所画图形绕点O旋转60°,你发现了什么?再旋转60°呢?
你能从图形运动的角度说明六边形ABCDEF是正六边形吗?
数学实验室
一般地,用量角器把一个圆n(n≥3)等分,依次连接各等分点所得的多边形是这个圆的内接正n边形.
这个圆是这个正n边形的外接圆.
正多边形的外接圆的圆心叫做正多边形的中心.
外接圆的半径叫做正多边形的半径.
概念认知
下图中的正多边形,哪些是轴对称图形?哪些是中心对称图形?如是轴对称图形,画出它的对称轴;如是中心对称图形,找出它的对称中心.
尝试与交流
通过上面的图形,你能发现正多边形有怎样的对称性?
正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过正n边形的中心.
归纳
思考:一个正多边形满足什么条件,该正多边形既是轴对称图形,又是中心对称图形?
一个正多边形,如果有偶数条边,那么它既是轴对称图形,又是中心对称图形.对称中心就是这个正多边形的中心.
归纳
1.请你想一想:用直尺和圆规,如何作一个正方形?
操作与思考
作法:(1)在⊙O中作两条互相垂直的直径AC、BD.
(2)依次连接A、B、C、D.
四边形ABCD就是所求作的正方形.
拓展思考:如何做正八边形?十六边形?
D
A
B
C
2.请你想一想:如果用直尺和圆规,如何作一个正六边形?
作法:(1)在⊙O中任意作一条直径AD.
(2)分别以点A、D为圆心,⊙O的半径为半径作弧,与⊙O相交于点B、F和点C、E.
(3)依次连接A、B、C、D、E、F各点.
正六边形ABCDEF就是所求作的正六边形.
拓展思考:如何作三角形?正十二边形?
A
B
C
F
O
D
E
例1 如图,正六边形ABCDEF的半径为4.求这个正六边形的周长和面积.
例题讲解
正六边形的面积
O
A
B
C
D
E
F
M
r
解:作半径OB、OC,过点O作OM⊥BC于M.
则正六边形的周长l=6×4=24.
则∠360°=60°.
r==24.
∵OB=OC,∴ △OBC是等边三角形.
在Rt△OMB中,OB=4,MB=
1.下列命题中,正确的说法有_________(填号).
①正多边形的各边相等;②各边相等的多边形是正多边形;③正多边形的各角相等;④各角相等的多边形是正多边形;⑤既是轴对称图形,又是中心对称的多边形是正多边形.
随堂演练
①
③
2.如图,⊙O是正五边形ABCDE的外接圆,则∠ADE的度数为( )
A.40° B.36° C.32° D.30°
B
3.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为( )
A.10 B.11 C.12 D.13
解:连接OA,OB,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=18°,
∴∠AOB=2∠ADB=36°,
∴这个正多边形的边数=
A
4.已知正四边形的外接圆的半径为1,则正四边形的周长是 .
4
课堂小结
正多边形与圆
正多边形和圆的关系
正n边形各顶点等分其外接圆.
正多边形的
有关概念
正多边形的中心.
正多边形的半径.
正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过正n边形的中心.
一个正多边形,如果有偶数条边,那么它既是轴对称图形,又是中心对称图形.对称中心就是这个正多边形的中心.
正多边形的对称性
第2章 对称图形——圆
2.6 正多边形与圆
1. n边形内角和公式
2. n边形外角概念.
n边形内角和=(n-2)·180°
3. n边形外角和等于360°.
知识回顾
说说有哪些你熟悉的图形?
情景引入
1.观察下列图形,你能说出这些图形的名称和特征吗?
各边相等、各角也相等的多边形叫做正多边形.
你能说说什么是正多边形吗?
获取新知
1. 请同学们举例,自己在日常生活中见过的正多边形.
2. 矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
思考与探索
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等.
1. 能否说各边相等的多边形是正多边形?
2. 能否说各角相等的多边形是正多边形?
注意
正多边形
缺一不可
各边相等
各角相等
1.如图,已知⊙O.
(1)用量角器把⊙O五等份,依次连接各等分点,得五边形ABCDE;
(2)五边形ABCDE是正五边形吗?为什么?
操作与思考
·
A
B
C
D
E
O
O
.
1.如图,已知⊙O.
(1)用量角器把⊙O五等份,依次连接各等分点,得五边形ABCDE;
(2)五边形ABCDE是正五边形吗?为什么?
操作与思考
·
A
B
C
D
E
O
如图,点A、B、C、D、E把⊙O五等分.
解:
∴ AB=BC=CD=DE=EA
⌒
⌒
⌒
⌒
⌒
∴AB=BC=CD=DE=EA,
BCE=CDA=3AB
⌒
⌒
⌒
∴∠A=∠B.
同理
∠B=∠C=∠D=∠E.
∴ 五边形ABCDE是正五边形.
2. 如图,点A、B、C、D、E、F六等分⊙O.
(1)在一张透明纸上画与下图形状、大小相同的图形,并把它们叠合在一起;
(2)把所画图形绕点O旋转60°,你发现了什么?再旋转60°呢?
你能从图形运动的角度说明六边形ABCDEF是正六边形吗?
数学实验室
一般地,用量角器把一个圆n(n≥3)等分,依次连接各等分点所得的多边形是这个圆的内接正n边形.
这个圆是这个正n边形的外接圆.
正多边形的外接圆的圆心叫做正多边形的中心.
外接圆的半径叫做正多边形的半径.
概念认知
下图中的正多边形,哪些是轴对称图形?哪些是中心对称图形?如是轴对称图形,画出它的对称轴;如是中心对称图形,找出它的对称中心.
尝试与交流
通过上面的图形,你能发现正多边形有怎样的对称性?
正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过正n边形的中心.
归纳
思考:一个正多边形满足什么条件,该正多边形既是轴对称图形,又是中心对称图形?
一个正多边形,如果有偶数条边,那么它既是轴对称图形,又是中心对称图形.对称中心就是这个正多边形的中心.
归纳
1.请你想一想:用直尺和圆规,如何作一个正方形?
操作与思考
作法:(1)在⊙O中作两条互相垂直的直径AC、BD.
(2)依次连接A、B、C、D.
四边形ABCD就是所求作的正方形.
拓展思考:如何做正八边形?十六边形?
D
A
B
C
2.请你想一想:如果用直尺和圆规,如何作一个正六边形?
作法:(1)在⊙O中任意作一条直径AD.
(2)分别以点A、D为圆心,⊙O的半径为半径作弧,与⊙O相交于点B、F和点C、E.
(3)依次连接A、B、C、D、E、F各点.
正六边形ABCDEF就是所求作的正六边形.
拓展思考:如何作三角形?正十二边形?
A
B
C
F
O
D
E
例1 如图,正六边形ABCDEF的半径为4.求这个正六边形的周长和面积.
例题讲解
正六边形的面积
O
A
B
C
D
E
F
M
r
解:作半径OB、OC,过点O作OM⊥BC于M.
则正六边形的周长l=6×4=24.
则∠360°=60°.
r==24.
∵OB=OC,∴ △OBC是等边三角形.
在Rt△OMB中,OB=4,MB=
1.下列命题中,正确的说法有_________(填号).
①正多边形的各边相等;②各边相等的多边形是正多边形;③正多边形的各角相等;④各角相等的多边形是正多边形;⑤既是轴对称图形,又是中心对称的多边形是正多边形.
随堂演练
①
③
2.如图,⊙O是正五边形ABCDE的外接圆,则∠ADE的度数为( )
A.40° B.36° C.32° D.30°
B
3.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为( )
A.10 B.11 C.12 D.13
解:连接OA,OB,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=18°,
∴∠AOB=2∠ADB=36°,
∴这个正多边形的边数=
A
4.已知正四边形的外接圆的半径为1,则正四边形的周长是 .
4
课堂小结
正多边形与圆
正多边形和圆的关系
正n边形各顶点等分其外接圆.
正多边形的
有关概念
正多边形的中心.
正多边形的半径.
正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过正n边形的中心.
一个正多边形,如果有偶数条边,那么它既是轴对称图形,又是中心对称图形.对称中心就是这个正多边形的中心.
正多边形的对称性
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
