苏科版数学九年级上册 第2章圆 单元复习 同步课件(共28张PPT)
文档属性
| 名称 | 苏科版数学九年级上册 第2章圆 单元复习 同步课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 304.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 11:11:16 | ||
图片预览





文档简介
第二章 对称图形——圆
单元复习
知识点一:圆的有关概念与性质
知识回顾
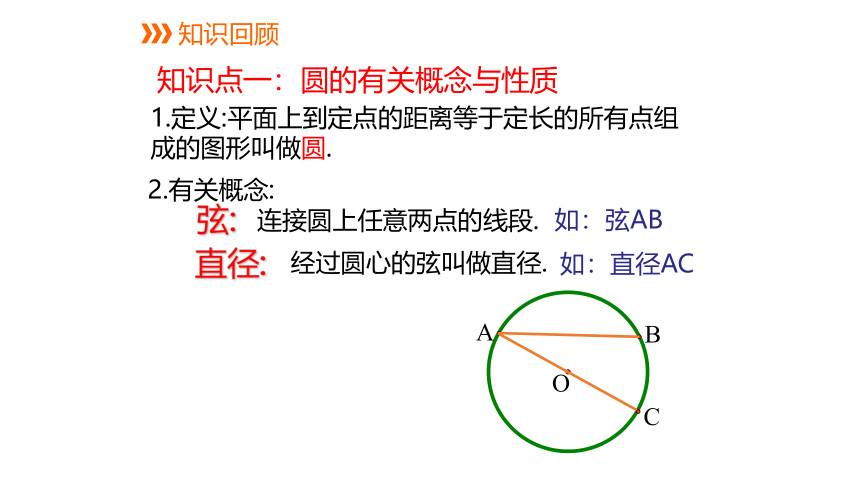
1.定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆.
2.有关概念:
弦:
连接圆上任意两点的线段.
O
A
B
C
直径:
经过圆心的弦叫做直径.
如:弦AB
如:直径AC
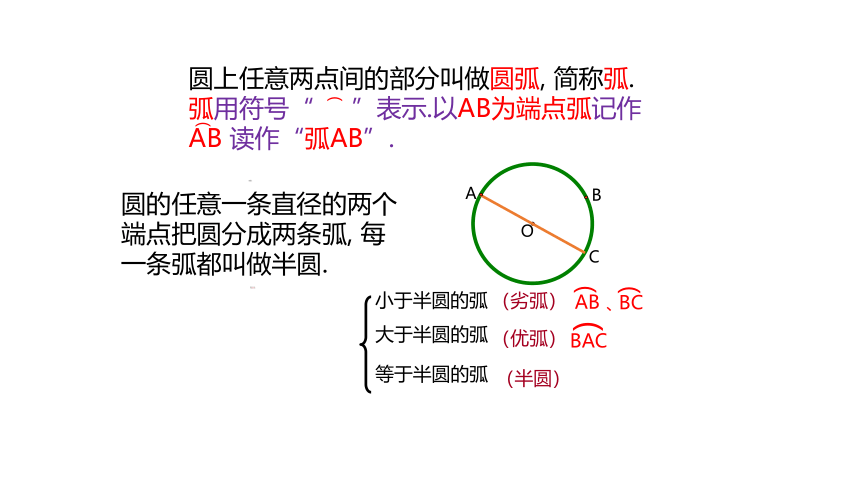
圆上任意两点间的部分叫做圆弧, 简称弧. 弧用符号“ ”表示.以AB为端点弧记作AB 读作“弧AB”.
O
B
C
(
(
半圆
圆的任意一条直径的两个端点把圆分成两条弧, 每一条弧都叫做半圆.
弧的分类
小于半圆的弧
大于半圆的弧
等于半圆的弧
(劣弧)
(优弧)
(半圆)
A
BAC
(
BC
(
AB 、
(
在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组都分别相等.
圆的对称性
圆心角的度数与它所对的弧的度数相等.
垂径定理: 垂直于弦的直径平分弦, 并且平分弦所对的两条弧.
圆周角和圆心角的关系
圆周角定理:
①圆周角的度数等于它所对弧上的圆心角度数的一半.
②同弧或等弧所对的圆周角相等.
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
圆内接四边形的对角互补.
不在同一条直线上的三点确定一个圆.
三角形的外接圆
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
1.(2021?西宁)如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=10,BE=2,则⊙O的半径OC= .
294
?
例题讲解
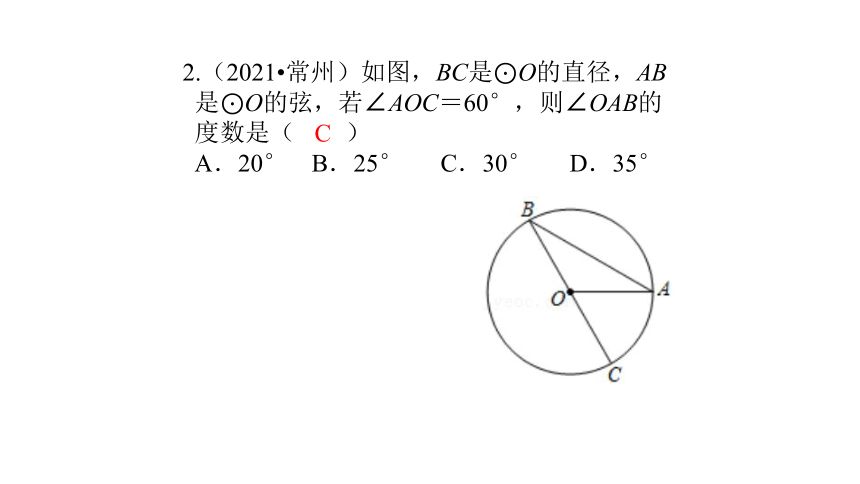
2.(2021?常州)如图,BC是⊙O的直径,AB是⊙O的弦,若∠AOC=60°,则∠OAB的度数是( ) A.20° B.25° C.30° D.35°
C
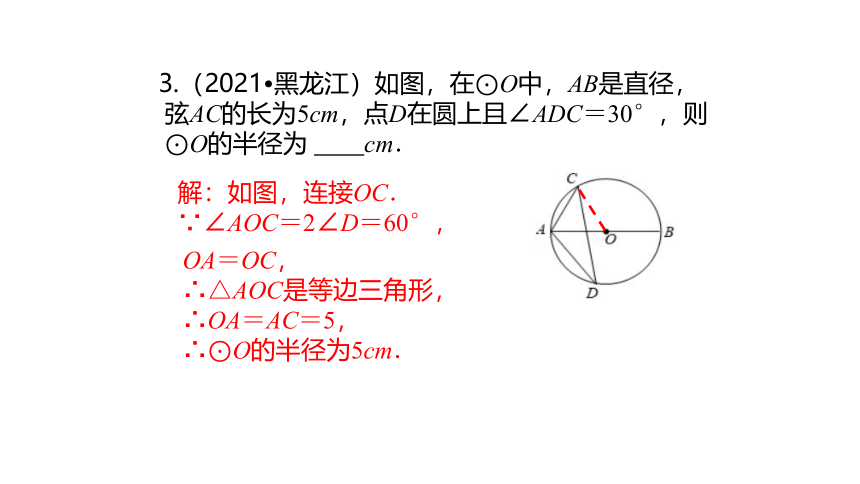
3.(2021?黑龙江)如图,在⊙O中,AB是直径,弦AC的长为5cm,点D在圆上且∠ADC=30°,则⊙O的半径为 cm.
解:如图,连接OC. ∵∠AOC=2∠D=60°,
OA=OC, ∴△AOC是等边三角形, ∴OA=AC=5, ∴⊙O的半径为5cm.
4.(2020?河北)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是( ) A.淇淇说的对,且∠A的另一个值是115° B.淇淇说的不对,∠A就得65° C.嘉嘉求的结果不对,∠A应得50° D.两人都不对,∠A应有3个不同值
D
5.(2021?西藏)如图,△BCD内接于⊙O,∠D=70°,OA⊥BC交?O于点A,连接AC,则∠OAC的度数为( ) A.40° B.55° C.70° D.110°
B
知识点二:与圆的有关的位置关系
点和圆的位置关系
点在圆内
点在圆上
点在圆外
d=r
d﹤r
d﹥r
2、直线与圆相切
1、直线与圆相交
3、直线与圆相离
dd=r
d>r
直线与圆的
位置关系
切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
切线的性质
圆的切线垂直于经过切点的半径.
三角形的内切圆
①三角形的内心是三角形角平分线的交点.
②三角形的内心到三边的距离相等.
与三角形各边都相切的圆叫三角形的内切圆.
三角形内切圆的圆心叫三角形的内心.
切线长定理
从圆外一点引圆的两条切线,它们的切线长相等.
1.点P是非圆上一点,若点P到⊙O上的点的最小距离是4cm,最大距离是9cm,则⊙O的半径是 __________________.
6.5cm或2.5cm
随堂演练
2.☉O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是( )
A.点A在☉O内部 B.点A在☉O上
C.点A在☉O外部 D.点A不在☉O上
D
3.(2021?临沂)如图,PA、PB分别与⊙O相切于A、B,∠P=70°,C为⊙O上一点,则∠ACB的度数为( ) A.110° B.120° C.125° D.130°
D
C
4.(2020?苏州)如图,已知AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD.若∠C=40°,则∠B的度数是 °.
25
5.(2021?通辽)如图,AB是⊙O的直径,过点A作⊙O的切线AC,点P是射线AC上的动点,连接OP,过点B作BD∥OP,交⊙O于点D,连接PD. 求证:PD是⊙O的切线.
证明:连接OD,
∵PA是⊙O的切线, ∴PA⊥AB,即∠PAO=90°,
∵BD∥OP, ∴∠B=∠AOP,∠BDO=∠DOP,
∵OB=OD, ∴∠BDO=∠B,
∴∠DOP=∠AOP,
在△AOP和△DOP中
∴△AOP≌△DOP(SAS),
????????=????????∠A????????=∠????????????????????=????????
?
∴∠PDO=∠PAO=90°,
?
即OD⊥PD,
∵OD是⊙O的半径, ∴PD是⊙O的切线.
半径为R的圆中,n°的圆心角所对的弧长l为
如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为
知识点三:与圆有关的计算
O
P
A
B
r
h
l
圆锥的侧面积和全面积
????侧=????????????
?
=
πrl +πr2
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( ) A.π B.2π C.3π D.6π
C
2.(2021?湖北)用半径为30cm,圆心角为120°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥底面半径为( ) A.5cm B.10cm C.15cm D.20cm
B
圆锥的底面圆周长=侧面展开后扇形的弧长.
3.(2021?盐城)设圆锥的底面半径为2,母线长为3,该圆锥的侧面积为 .
6π
?
4.(2021?哈尔滨)一个扇形的弧长是8πcm,圆心角是144°,则此扇形的半径是 cm.
10
?
5.(2021?扬州改编)如图,四边形ABCD中,AD∥BC,∠BAD=90°,CB=CD,连接BD,以点B为圆心,BA长为半径作⊙B,交BD于点E. (1)试判断CD与⊙B的位置关系,并说明理由;
F
解:(1)过点B作BF⊥CD,垂足为F, ∵AD∥BC, ∴∠ADB=∠CBD, ∵CB=CD, ∴∠CBD=∠CDB, ∴∠ADB=∠CDB.
在△ABD和△FBD中
∴△ABD≌△FBD(AAS),
∠????????????=∠????????????∠A????????=∠????????????????????=????????
?
F
∴BF=BA,则点F在圆B上, ∴CD与⊙B相切;
5.(2021?扬州改编)如图,四边形ABCD中,AD∥BC,∠BAD=90°,CB=CD,连接BD,以点B为圆心,BA长为半径作⊙B,交BD于点E.
(2)若AD=2,∠BCD=60°,求图中阴影部分的面积.
F
阴影部分的面积
=S△ABD﹣S扇形ABE
=12×2×23?30????(23)2360
?
=23?π.
?
课堂小结
圆
圆的有关性质
垂径定理
圆周角定理
与圆有关的位置关系
点与圆的位置关系
直线与圆的位置的关系
与圆有关的计算
正多边形和圆
弧长和扇形
圆锥的侧面积
单元复习
知识点一:圆的有关概念与性质
知识回顾
1.定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆.
2.有关概念:
弦:
连接圆上任意两点的线段.
O
A
B
C
直径:
经过圆心的弦叫做直径.
如:弦AB
如:直径AC
圆上任意两点间的部分叫做圆弧, 简称弧. 弧用符号“ ”表示.以AB为端点弧记作AB 读作“弧AB”.
O
B
C
(
(
半圆
圆的任意一条直径的两个端点把圆分成两条弧, 每一条弧都叫做半圆.
弧的分类
小于半圆的弧
大于半圆的弧
等于半圆的弧
(劣弧)
(优弧)
(半圆)
A
BAC
(
BC
(
AB 、
(
在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组都分别相等.
圆的对称性
圆心角的度数与它所对的弧的度数相等.
垂径定理: 垂直于弦的直径平分弦, 并且平分弦所对的两条弧.
圆周角和圆心角的关系
圆周角定理:
①圆周角的度数等于它所对弧上的圆心角度数的一半.
②同弧或等弧所对的圆周角相等.
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
圆内接四边形的对角互补.
不在同一条直线上的三点确定一个圆.
三角形的外接圆
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
1.(2021?西宁)如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=10,BE=2,则⊙O的半径OC= .
294
?
例题讲解
2.(2021?常州)如图,BC是⊙O的直径,AB是⊙O的弦,若∠AOC=60°,则∠OAB的度数是( ) A.20° B.25° C.30° D.35°
C
3.(2021?黑龙江)如图,在⊙O中,AB是直径,弦AC的长为5cm,点D在圆上且∠ADC=30°,则⊙O的半径为 cm.
解:如图,连接OC. ∵∠AOC=2∠D=60°,
OA=OC, ∴△AOC是等边三角形, ∴OA=AC=5, ∴⊙O的半径为5cm.
4.(2020?河北)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是( ) A.淇淇说的对,且∠A的另一个值是115° B.淇淇说的不对,∠A就得65° C.嘉嘉求的结果不对,∠A应得50° D.两人都不对,∠A应有3个不同值
D
5.(2021?西藏)如图,△BCD内接于⊙O,∠D=70°,OA⊥BC交?O于点A,连接AC,则∠OAC的度数为( ) A.40° B.55° C.70° D.110°
B
知识点二:与圆的有关的位置关系
点和圆的位置关系
点在圆内
点在圆上
点在圆外
d=r
d﹤r
d﹥r
2、直线与圆相切
1、直线与圆相交
3、直线与圆相离
d
d>r
直线与圆的
位置关系
切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
切线的性质
圆的切线垂直于经过切点的半径.
三角形的内切圆
①三角形的内心是三角形角平分线的交点.
②三角形的内心到三边的距离相等.
与三角形各边都相切的圆叫三角形的内切圆.
三角形内切圆的圆心叫三角形的内心.
切线长定理
从圆外一点引圆的两条切线,它们的切线长相等.
1.点P是非圆上一点,若点P到⊙O上的点的最小距离是4cm,最大距离是9cm,则⊙O的半径是 __________________.
6.5cm或2.5cm
随堂演练
2.☉O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是( )
A.点A在☉O内部 B.点A在☉O上
C.点A在☉O外部 D.点A不在☉O上
D
3.(2021?临沂)如图,PA、PB分别与⊙O相切于A、B,∠P=70°,C为⊙O上一点,则∠ACB的度数为( ) A.110° B.120° C.125° D.130°
D
C
4.(2020?苏州)如图,已知AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD.若∠C=40°,则∠B的度数是 °.
25
5.(2021?通辽)如图,AB是⊙O的直径,过点A作⊙O的切线AC,点P是射线AC上的动点,连接OP,过点B作BD∥OP,交⊙O于点D,连接PD. 求证:PD是⊙O的切线.
证明:连接OD,
∵PA是⊙O的切线, ∴PA⊥AB,即∠PAO=90°,
∵BD∥OP, ∴∠B=∠AOP,∠BDO=∠DOP,
∵OB=OD, ∴∠BDO=∠B,
∴∠DOP=∠AOP,
在△AOP和△DOP中
∴△AOP≌△DOP(SAS),
????????=????????∠A????????=∠????????????????????=????????
?
∴∠PDO=∠PAO=90°,
?
即OD⊥PD,
∵OD是⊙O的半径, ∴PD是⊙O的切线.
半径为R的圆中,n°的圆心角所对的弧长l为
如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为
知识点三:与圆有关的计算
O
P
A
B
r
h
l
圆锥的侧面积和全面积
????侧=????????????
?
=
πrl +πr2
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( ) A.π B.2π C.3π D.6π
C
2.(2021?湖北)用半径为30cm,圆心角为120°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥底面半径为( ) A.5cm B.10cm C.15cm D.20cm
B
圆锥的底面圆周长=侧面展开后扇形的弧长.
3.(2021?盐城)设圆锥的底面半径为2,母线长为3,该圆锥的侧面积为 .
6π
?
4.(2021?哈尔滨)一个扇形的弧长是8πcm,圆心角是144°,则此扇形的半径是 cm.
10
?
5.(2021?扬州改编)如图,四边形ABCD中,AD∥BC,∠BAD=90°,CB=CD,连接BD,以点B为圆心,BA长为半径作⊙B,交BD于点E. (1)试判断CD与⊙B的位置关系,并说明理由;
F
解:(1)过点B作BF⊥CD,垂足为F, ∵AD∥BC, ∴∠ADB=∠CBD, ∵CB=CD, ∴∠CBD=∠CDB, ∴∠ADB=∠CDB.
在△ABD和△FBD中
∴△ABD≌△FBD(AAS),
∠????????????=∠????????????∠A????????=∠????????????????????=????????
?
F
∴BF=BA,则点F在圆B上, ∴CD与⊙B相切;
5.(2021?扬州改编)如图,四边形ABCD中,AD∥BC,∠BAD=90°,CB=CD,连接BD,以点B为圆心,BA长为半径作⊙B,交BD于点E.
(2)若AD=2,∠BCD=60°,求图中阴影部分的面积.
F
阴影部分的面积
=S△ABD﹣S扇形ABE
=12×2×23?30????(23)2360
?
=23?π.
?
课堂小结
圆
圆的有关性质
垂径定理
圆周角定理
与圆有关的位置关系
点与圆的位置关系
直线与圆的位置的关系
与圆有关的计算
正多边形和圆
弧长和扇形
圆锥的侧面积
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
