苏科版数学九年级上册 1.3 一元二次方程根与系数的关系 同步课件(共16张PPT)
文档属性
| 名称 | 苏科版数学九年级上册 1.3 一元二次方程根与系数的关系 同步课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 337.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 00:00:00 | ||
图片预览






文档简介
第1章 一元二次方程
1.3 一元二次方程根与系数的关系
1.一元二次方程的一般形式是什么?
2.当 时,方程的解是什么?
求根公式:
知识回顾
ax?+bx+c=0
x?-3x+2=0
x?+3x+2=0
x?-5x+6=0
x?+5x+6=0
x?-2x=0
1
2
3
2
2
-2
-3
-1
6
3
5
2
-2
-3
-5
6
0
2
2
0
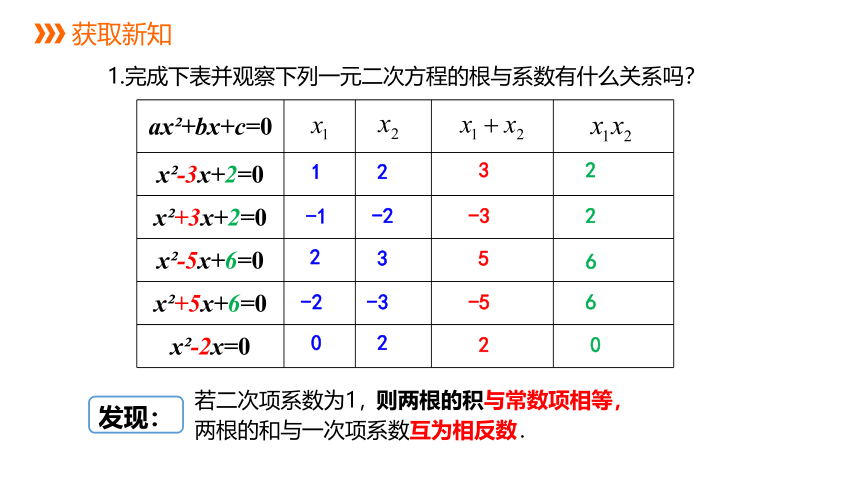
1.完成下表并观察下列一元二次方程的根与系数有什么关系吗?
若二次项系数为1,
则两根的积与常数项相等,
两根的和与一次项系数互为相反数.
获取新知
发现:
2.方程 的两根是
这两根的和、两根的积与系数有什么关系?
3.先求出方程 的解,再验证这个方程的两根与系数是否具有你刚刚发现的关系.
思考:如果一元二次方程 ax2+bx+c=0 (a≠0),
的两个根分别x1、x2,那么它们的和与差与系数有什么关系?
你能证明刚才的发现吗?
一元二次方程 ax2+bx+c=0 (a≠0),
当 b2-4ac≥0 时,它的两个根分别是 x1、x2.
设它的两个根分别是 x1、x2,那么
这就是一元二次方程根与系数的关系(也叫韦达定理)
一元二次方程 ax2+bx+c=0 (a≠0)当 b2-4ac≥0 时,
归纳总结
一元二次方程的根与系数有如下关系:
对于一元二次方程 ax2+bx+c=0 (a≠0)
两根之和等于一次项系数b除以二次项系数a的商的相反数;
两根之积等于常数项c除以二次项系数a所得的商.
当二次项系数不为1时,
两根之和等于一次项系数b的相反数;
两根之积等于常数项c.
特别地,二次项系数为1时,方程变为x2+bx+c=0
语言描述
(1)x2+2x-5=0; (2)2x2+x=1.
例题讲解
例1:求下列方程两根的和与两根的积:
解:(1)设方程的两根分别是x1、x2.
∵ a=1,b=2,c=?5,
?
∴??x1 + x2 = ?????????=?2 ,
?
??????x1 ?x2 = ????????=?5 .
?
(2)把方程化成一般形式,得
2????2+?????1=0.
?
∵ a=2,b=1,c=?1,
?
∴??x1 + x2 = ?????????=?12 ,
?
??????x1 ?x2 = ????????=?12 .
?
设方程的两根分别是x1、x2.
例2:求下列方程两根的和与两根的积: x2+2x+2=0.
解:∵ a=1,b=2,c=2,
?
b2-4ac=22-4×1×2=-4<0,
∴方程没有实数根.
?
能直接套用公式吗?
则不存在方程两根之和与两根之积.
?
在使用根与系数的关系时,应注意:
(2)利用公式的前提条件为 b2-4ac≥0;
(3)在使用 时,注意“-”不要漏写.
(1)方程要先化成一般式;
点拨
例3:已知方程 5x2+kx?6=0的一个根是2,求它的另一个根及k的值.
?
解:∵ a=5,b=????,c=?6,
?
设方程的两根分别是x1、2.
∴??x1 + 2= ?????????=?????5 ,
?
?????2x1 = ????????=?65 .
?
∴??x1 = ?35 ,k=?7.
?
1. 求下列方程两根的和与两根的积:
随堂演练
x1 + x2 = 4 ,
??????x1 ?x2 = 1.
?
?x1 + x2 = 32 ,
?
??????x1 ?x2 = ?1.
?
?x1 + x2 = ?23 ,
?
??????x1 ?x2 = 0.
?
x1 + x2 = 0 ,
??????x1 ?x2 = ?14.
?
2. 下列结论是否正确?
(1)?错? x1 + x2 = ?????????=?5 ;
?
(2)?错? x1 ? x2 = ????????=?1 .
?
你能写出这个方程中被墨迹污染的一次项系数和常数项吗?
3.小明在一本课外读物中读到如下一段文字:
一元二次方程x2- x =0 的两根是 和 .
解:∵a=1, x1 + x2 = ?????????=????? ,
?
∴2+3+2?3= =?????,2+32?3=????.
?
∴??????=?4,????=1.
?
??????x1 ?x2 = ????????=???? .
?
∴一次项系数是?4,常数项是1.
?
课堂小结
根与系数的关系
(韦达定理)
内 容
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么
注意
方程要先化成一般式
利用公式的前提条件为 b2-4ac≥0
在计算两根系数之和时不要丢掉负号
1.3 一元二次方程根与系数的关系
1.一元二次方程的一般形式是什么?
2.当 时,方程的解是什么?
求根公式:
知识回顾
ax?+bx+c=0
x?-3x+2=0
x?+3x+2=0
x?-5x+6=0
x?+5x+6=0
x?-2x=0
1
2
3
2
2
-2
-3
-1
6
3
5
2
-2
-3
-5
6
0
2
2
0
1.完成下表并观察下列一元二次方程的根与系数有什么关系吗?
若二次项系数为1,
则两根的积与常数项相等,
两根的和与一次项系数互为相反数.
获取新知
发现:
2.方程 的两根是
这两根的和、两根的积与系数有什么关系?
3.先求出方程 的解,再验证这个方程的两根与系数是否具有你刚刚发现的关系.
思考:如果一元二次方程 ax2+bx+c=0 (a≠0),
的两个根分别x1、x2,那么它们的和与差与系数有什么关系?
你能证明刚才的发现吗?
一元二次方程 ax2+bx+c=0 (a≠0),
当 b2-4ac≥0 时,它的两个根分别是 x1、x2.
设它的两个根分别是 x1、x2,那么
这就是一元二次方程根与系数的关系(也叫韦达定理)
一元二次方程 ax2+bx+c=0 (a≠0)当 b2-4ac≥0 时,
归纳总结
一元二次方程的根与系数有如下关系:
对于一元二次方程 ax2+bx+c=0 (a≠0)
两根之和等于一次项系数b除以二次项系数a的商的相反数;
两根之积等于常数项c除以二次项系数a所得的商.
当二次项系数不为1时,
两根之和等于一次项系数b的相反数;
两根之积等于常数项c.
特别地,二次项系数为1时,方程变为x2+bx+c=0
语言描述
(1)x2+2x-5=0; (2)2x2+x=1.
例题讲解
例1:求下列方程两根的和与两根的积:
解:(1)设方程的两根分别是x1、x2.
∵ a=1,b=2,c=?5,
?
∴??x1 + x2 = ?????????=?2 ,
?
??????x1 ?x2 = ????????=?5 .
?
(2)把方程化成一般形式,得
2????2+?????1=0.
?
∵ a=2,b=1,c=?1,
?
∴??x1 + x2 = ?????????=?12 ,
?
??????x1 ?x2 = ????????=?12 .
?
设方程的两根分别是x1、x2.
例2:求下列方程两根的和与两根的积: x2+2x+2=0.
解:∵ a=1,b=2,c=2,
?
b2-4ac=22-4×1×2=-4<0,
∴方程没有实数根.
?
能直接套用公式吗?
则不存在方程两根之和与两根之积.
?
在使用根与系数的关系时,应注意:
(2)利用公式的前提条件为 b2-4ac≥0;
(3)在使用 时,注意“-”不要漏写.
(1)方程要先化成一般式;
点拨
例3:已知方程 5x2+kx?6=0的一个根是2,求它的另一个根及k的值.
?
解:∵ a=5,b=????,c=?6,
?
设方程的两根分别是x1、2.
∴??x1 + 2= ?????????=?????5 ,
?
?????2x1 = ????????=?65 .
?
∴??x1 = ?35 ,k=?7.
?
1. 求下列方程两根的和与两根的积:
随堂演练
x1 + x2 = 4 ,
??????x1 ?x2 = 1.
?
?x1 + x2 = 32 ,
?
??????x1 ?x2 = ?1.
?
?x1 + x2 = ?23 ,
?
??????x1 ?x2 = 0.
?
x1 + x2 = 0 ,
??????x1 ?x2 = ?14.
?
2. 下列结论是否正确?
(1)?错? x1 + x2 = ?????????=?5 ;
?
(2)?错? x1 ? x2 = ????????=?1 .
?
你能写出这个方程中被墨迹污染的一次项系数和常数项吗?
3.小明在一本课外读物中读到如下一段文字:
一元二次方程x2- x =0 的两根是 和 .
解:∵a=1, x1 + x2 = ?????????=????? ,
?
∴2+3+2?3= =?????,2+32?3=????.
?
∴??????=?4,????=1.
?
??????x1 ?x2 = ????????=???? .
?
∴一次项系数是?4,常数项是1.
?
课堂小结
根与系数的关系
(韦达定理)
内 容
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么
注意
方程要先化成一般式
利用公式的前提条件为 b2-4ac≥0
在计算两根系数之和时不要丢掉负号
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
